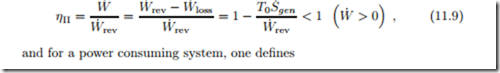Reversible Work and Second Law Efficiency
A sometimes useful measure2 for the performance of a system is the second law efficiency ηII, which compares the actual performance to the reversible work, i.e., the best case scenario for the same process parameters.
The reversible work W˙ rev is the power that would be obtained from a reversible process operating under the same boundary conditions as the system considered, and exchanging heat with the environment at T0. Its value follows from (11.4) simply by setting the irreversibility to zero, T0S˙gen = 0,
Since all irreversibilities reduce the process performance, for a work generating process the reversible work is the maximum work that could be obtained, and for a work consuming process it is the minimum work required. The actual work can be expressed as the difference between reversible work and work loss, W˙ = W˙ rev − W˙ loss.
The second law efficiency is defined as the ratio between the actual work of the process and the reversible work. For a power producing system one defines
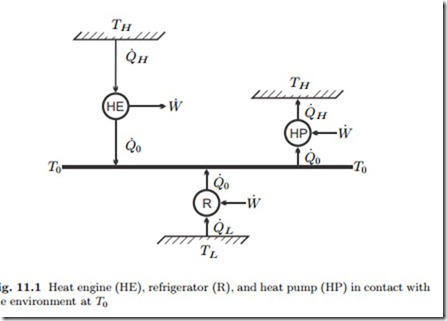
The simplest examples are given by steady state engines operating be- tween two reservoirs at constant temperatures, and we consider heat engine, refrigerator, and heat pump, as depicted in Fig. 11.1. Note that all engines exchange heat with the environment at T0, while the temperatures of the other reservoirs are different. The fully reversible engines operating between two reservoirs are Carnot engines.
For a heat engine that receives the heat Q˙ H from a hot reservoir at TH > T0, and rejects heat into the environment at T0, actual and reversible work
where η = W˙ /Q˙ H is the thermal efficiency of the actual engine, and ηC = W˙ rev /Q˙ H = 1 − T0 is the thermal efficiency of a fictional Carnot heat engine operating between the same temperatures. It is straightforward to conclude that for a more complex power producing system ηII = η/ηrev where ηrev is the thermal efficiency associated with the reversible work.
To summarize, we state that the second law efficiency gives a qualitative measure for the overall quality of a process by comparing actual performance to that of a fictional reversible system with the same parameters..