Performance characteristics for low-speed machines
The operating condition of a turbomachine will be dynamically similar at two different rotational speeds if all fluid velocities at corresponding points within the machine are in the same direction and proportional to the blade speed. In other words, the flow is dynamically similar if the stream- line patterns relative to the blades are geometrically similar. When two flow fields are dynamically similar, then all the dimensionless groups are the same. As shown by Eqs. (2.3a-c), for an incompressible flow machine (one in which M , 0.3 everywhere) operating at high Reynolds number, dynamic similarity is achieved once the flow coefficient is the same. Thus, the nondimensional pre- sentation of performance data has the important practical advantage of collapsing results into a single curve that would otherwise require a multiplicity of curves if plotted dimensionally.
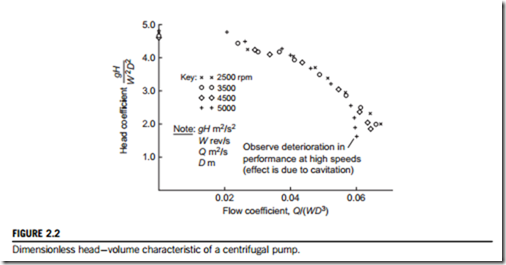
Evidence in support of the foregoing assertion is provided in Figure 2.2, which shows experimental results obtained by one author (at the University of Liverpool) on a simple centrifugal laboratory pump. Within the normal operating range of this pump, 0.03 , Q/(ΩD3) , 0.06, very little systematic scatter is apparent, which might be associated with a Reynolds number effect, for the range of speeds 2500 # Ω # 5000 rpm. For smaller flows, Q/(ΩD3) , 0.025, the flow became unsteady and the manometer readings of uncertain accuracy, but nevertheless, dynamically similar
conditions still appear to hold true. At high flow rates there is a systematic deviation away from the “single-curve” law at higher rotational speeds. This effect is due to cavitation, a high-speed phenomenon of hydraulic machines caused by the release of vapor bubbles at low pressures, which is discussed later in this chapter. It will be clear at this stage that under cavitating flow conditions, dynamical similarity is not possible.
The nondimensional results shown in Figure 2.2 have, of course, been obtained for a particular pump. They would also be approximately valid for a range of different pump sizes so long as all these pumps are geometrically similar and cavitation is absent. Thus, neglecting any change in per- formance due to change in Reynolds number, the dynamically similar results in Figure 2.2 can be applied to predicting the dimensional performance of a given pump for a series of required speeds. Figure 2.3 shows such a dimensional presentation. It will be clear from the preceding discussion that the locus of dynamically similar points in the H-Q field lies on a parabola since H varies as Ω2 and Q varies as Ω.
EXAMPLE 2.1
A model centrifugal pump with an efficiency of 88% is tested at a rotational speed of 3000 rpm and delivers 0.12 m3/s of water against a head of 30 m. Using the similarity rules given above, determine the rotational speed, volume flow rate, and power requirement of a geometrically similar prototype at eight times the scale of the model and working against a head of 50 m.
Solution
From the similarity laws, for the same head coefficient,