Sub- and Supersonic Flows
Gas flows through nozzles and diffusers show an interesting behavior when their speed reaches, or is above, the speed of sound of the gas. This behavior must be well understood for the proper design of devices and engines. In this section we study the laws that govern the transition from sub- to supersonic flow and vice-versa, and draw relevant conclusions for the design of nozzles and diffusers, and for rocket motors. We will see that subsonic nozzles have a converging cross section, while supersonic nozzles have a converging-diverging cross section.
Speed of Sound
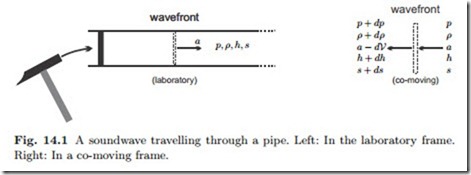
The ear reacts to small pressure oscillations,1 that is sound is a pressure wave. The speed of sound is the speed with which such a small pressure disturbance travels through a medium. To compute its value, we consider a simple experiment, shown in Fig. 14.1 (left): In a long pipe, a wave is created by a small push of a piston. This wave travels through the pipe with the speed of sound, a.
To analyze the wave, and to compute the speed of sound, it is best to consider the wavefront from a co-moving frame, as depicted on the right of the figure. The wave travels into undisturbed fluid with properties p, ρ, h, s, and the observer travelling with the wave sees fluid coming in at the speed of sound a. The fluid left behind by the wave has slightly altered properties p + dp, ρ + dρ, h + dh, s + ds, and the observer on the wave sees it leaving with speed a − dV.
Since the wave travels fast, there is no time for heat exchange, thus we can assume that the wave is adiabatic. Moreover, we shall ignore irreversibilities through friction, that is we consider reversible wave propagation.
Indeed, sound waves in air are only very weakly damped. That we hear noises from far away only weakly is due to the spherical propagation of sound waves, where the sound energy is distributed over shells of surface 4πR2 when R is the distance from the sound source. Thus local sound energy, which is what we hear, is inversely proportional to the square of the distance from the source, that is proportional to 1/R2. In a pipe, however, the propagation is one-dimensional, waves travel as plane waves with unchanged wave surface area, which is equal to the pipe cross section.
Applying the mass balance to the wave front yields
where the subscript s indicates that the derivative must be taken at constant entropy.