Laval Nozzle
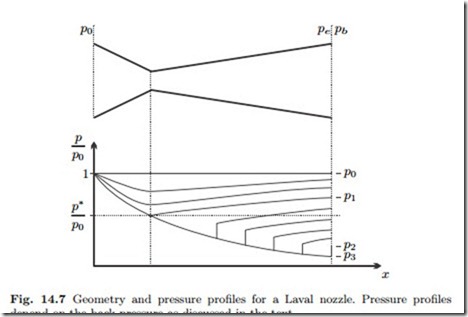
To reach exit velocities above the speed of sound requires converging- diverging nozzles, which will be discussed next. The cross section A is first decreasing until is reaches its smallest value Ath in the throat of the nozzle, and then it is increasing to the exit cross section Ae. Again we consider the pressure distribution in the nozzle which results from lowering the back pressure pb, see Fig. 14.7.
When pb = p0, there is no flow and homogenous pressure p0 throughout the nozzle. When the back pressure is lowered somewhat, a flow occurs. According to Fig. 14.4, the flow function is hill-shaped, and the nozzle feed state is on the right foot of that hill, at p = p0, ψ = 0. Since Aψ p is constant, the flow function must grow—go uphill—in the converging part of the nozzle, and it must decrease—go downhill—in the diverging part.
We first consider relatively large back pressures in the pressure range p1 < pb < p0 in the figure. As the nozzle converges, the flow state climbs uphill until a value pth > p∗, ψth < ψ∗ is reached in the throat. This point is to the right of the maximum. As the cross section grows in the diverging part, the flow function must decrease, and this is only possible by returning to higher pressures, that is by going back downhill towards the right. The flow is accelerated in the converging part of the nozzle, and decelerated in the diverging part, the outflow velocity is relatively low, and subsonic. The extreme case of this flow type is reached for pb = p1, when the air is in the critical state in the throat—on top of the hill with sonic speed—but then is decelerated again.
When the flow reaches the critical state in the throat, the flow function can decrease by going down the left side of the hill, towards lower pressures, and higher, i.e., supersonic, velocities. As indicated in the figure, this requires low back pressures p2 < pb ≤ 0. In this range the flow is isentropic inside the nozzle. If the back pressure is just at p3, the end pressure is equal to the back pressure, and no external irreversibilities occur. If the back pressure is in the range p2 < pb < p3, the end pressure is below the back pressure and pressure is equilibrated through oblique shocks outside the nozzle. For lower back pressures pb < p3, the end pressure is above the back pressure and pressure is equilibrated through external expansion waves.
In the range p2 < pb < p1, isentropic flow inside the nozzle is not possible. The flow will follow isentropic flow conditions for a while, accelerating to supersonic flow behind the throat, and then a irreversible normal shock will occur, that is a sudden jump from low pressure supersonic flow to high pressure subsonic flow. Behind the shock, the flow will be isentropic again, and the gas will expand to the back pressure.
We shall not further discuss normal and oblique shocks, but stress that they are strongly irreversible, and thus reduce nozzle efficiency substantially.
In a shock, the flow changes from supersonic to subsonic, which means significant reduction of thrust. Nozzle geometry must be carefully designed so that the flow conditions are optimal. Some supersonic aircraft have nozzles with variable geometry, to adjust for the wide range of back pressures encountered between take-off and high altitude flight.