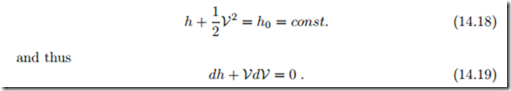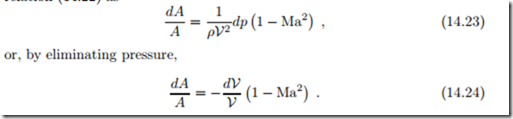Compressible Flow,Nozzles and Diffusers:Area-Velocity Relation

Area-Velocity Relation

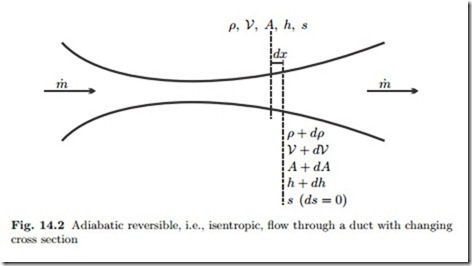
The main design parameter for nozzles and diﬀusers is the change of cross section, and we ask how ﬂow properties, in particular velocity and pressure, change with the cross section. Figure 14.2 shows an adiabatic and reversible, i.e., isentropic, ﬂow through a duct with varying cross section. We consider a small slice of the duct of width dx, and apply the balances of mass, energy and entropy, similar to what we did for the wave in the pipe above.

Here, h0 is the stagnation enthalpy, deﬁned as the enthalpy the ﬂow would obtain when brought to rest adiabatically. Since the ﬂow is isentropic, we have ds = 0, and the Gibbs equation gives

Elimination of enthalpy between the last two equations yields the relation between pressure and velocity changes in isentropic nozzles and diﬀusers,

which we discussed already in Sec. 9.11. We use this to eliminate V from the mass balance to ﬁnd

where the subscript indicates isentropic ﬂow.

To proceed, we introduce the Mach number

which compares ﬂow velocity to speed of sound: Ma < 1 for subsonic ﬂows, Ma > 1 for supersonic ﬂows, and Ma = 1 for sonic ﬂows. Flows with Ma » 1 are called hypersonic and ﬂows with Ma ‘"" 1 are called transonic.

With the deﬁnition (14.10) of the speed of sound we thus can write the relation (14.22) as

Equations (14.23) and (14.24) are the area-pressure relation and the area- velocity relation for isentropic duct ﬂows. Both relations carry the factor (1 − Ma2) which has diﬀerent sign for subsonic and supersonic ﬂows.

Accordingly, a change of cross section has diﬀerent eﬀect when applied to sub- and supersonic ﬂows.

Subsonic Flows (Ma<1): For a converging duct we have from (14.23, 14.24)

the ﬂow is accelerated while pressure drops; this is a nozzle.

In other words, a converging duct acts as a nozzle in subsonic ﬂow, but as a diﬀuser in supersonic ﬂow. A diverging duct acts as a diﬀuser in subsonic ﬂow, but as a nozzle in supersonic ﬂow. Figure 14.3 shows a summary.