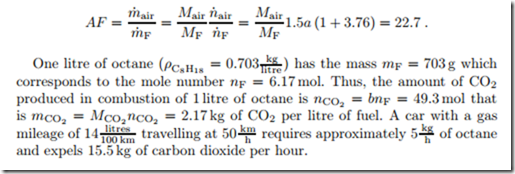Combustion Air
Most combustion processes use air as an oxidizer, which is freely available for most applications, e.g., stationary power plants or air breathing engines for cars and airplanes. Rockets fly at high altitudes or in space where the oxygen density is low or zero and thus they must bring their oxidizer along. To reduce payload, rocket engines are fed with fuel and pure oxygen, or with solid oxidizer-fuel compounds, e.g., ammonium perchlorate and aluminium powder.
For combustion with air, the oxygen is accompanied by the other components of air. Since oxygen and nitrogen are the two main ingredients, in combustion analysis one normally ignores the other components, and considers air as a mixture of oxygen and nitrogen with XO2 = 0.21 and XN2 = 0.79.
Thus, in dry air for one mole of oxygen 1 XO2 = 4.76 moles of air are required, that is each mole of oxygen is accompanied by 3.76 moles of nitrogen.
Due to the presence of nitrogen, nitrogen oxides (NOx) may form in the combustion processes which are toxic. Since the amounts are small, the formation of NOx will be ignored below, but due to the toxicity the formation of NOx must be monitored, and suppressed, in practice.
The amount of oxygen that is required for complete combustion of a fuel is known as the stoichiometric amount, the corresponding amount of air is denoted as stoichiometric air or as theoretical air. For the general hydrocarbon reaction (25.1) the stoichiometric air is 14.76 (x + y )l moles of air per mole of fuel. Often the air amount is given as percent of theoretical air, for instance 150% of theoretical air corresponds to 17.14 (x + y )l moles of air per mole of fuel, or to 50% of excess air .
Example: Mole and Mass Flow Balances
As an example we consider the combustion of a mass flow m˙ F = 5 kg of octane (C8H18) with 150% theoretical air. We ask for the mass flow of air required, and the mass flows of the products. Since chemical balances concern mole numbers rather than masses, we first determine the mole flow of fuel as
The required amount of air, and the resulting amount of product, is deter- mined by writing a chemical equation for all involved components as
Here, a is the amount of oxygen required for the stoichiometric combustion per mole of fuel, the factor 1.5 on the left accounts for 150% of theoretical air. The first term on the right is the unused portion of oxygen, which is total oxygen coming in (1.5a) minus the stoichiometric amount (a). The numbers a, b, c, d must be determined from balancing the elements C, H, O and N, on both sides of the equation. This gives