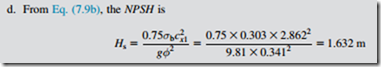Design of a pump inlet
A crucial factor in good pump design is the avoidance of cavitation both on account of obtaining good efficiency and the possibility of damage to the impeller blades. In Chapter 2, a brief description of cavitation was given and the net positive suction head, NPSH, was defined as
where p0 is the absolute stagnation pressure of the liquid and pv is its absolute vapor pressure.
The pump considered in the following analysis is assumed to have the flow geometry shown in Figure 7.4. As liquid passes through the impeller, there are changes in the pressure levels. In the vicinity of the impeller blades’ leading edges on the suction surfaces there will be a rapid increase in velocity and a corresponding decrease in pressure. If the absolute pressure of the liquid drops below the vapor pressure then cavitation will occur. The fluid then moves into the impeller and the dynamic action of the blades causes the pressure to increase. This pressure rise causes the cavita- tion bubbles’ collapse and the resulting implosion of the bubbles and consequent shock waves can cause pitting of the impeller blades and, eventually, structural failure.
Cavitation can also occur near the impeller exit of radial flow and mixed flow impellers where the velocities are greatest. The blade tip of the axial-flow pump has been found to be the most vulnerable location for cavitation. At inception of cavitation, at some point on the surface of the pump the pressure is equal to the vapor pressure, i.e.,
where σb is the blade cavitation coefficient corresponding to the cavitation point.
Figure 9.20 is an example of the severe cavitation damage sustained by the runner of a Francis turbine. Similar damage can occur in pump impellers. Pearsall (1972) found that this coefficient lies in the range
EXAMPLE 7.1
The inlet of a centrifugal pump of the type shown in Figure 7.4 is to be designed for optimum conditions when the flow rate of water is 25 dm3/s and the impeller rotational speed is 1450 rev/min. The maximum suction specific speed Ωss 5 3.0 (rad) and the inlet eye radius ratio is to be 0.3. Determine
a. the blade cavitation coefficient;
b. the shroud diameter at the eye;
c. the eye axial velocity;
d. the NPSH.
Solution
a. From Eq. (7.9c), squaring both sides,