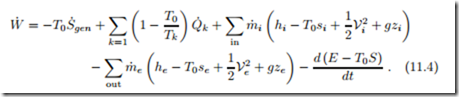Irreversibility and Work Loss
In the discussion of work losses for closed and open systems we found that irreversibilities reduce the efficiency of energy conversion, see Sec. 5.10. We shall study this now in greater detail. The arguments used in this section are similar to “exergy accounting” (see Sec. 11.8 further below).
We consider a general thermodynamic system as in Fig. 9.1 which is de- scribed through the balance laws for mass, energy, and entropy (9.1, 9.9, 9.10). Part of the heat exchange between the system and its surroundings will take place at a temperature T0, and we write
The highlighted temperature T0 can be freely chosen according to the de- tails of the actual system considered. Since most thermodynamic systems interact with the environment, one most often chooses T0 to be the temperature of the environment, usually T0 = 298 K for the standard reference environment. Indeed, the environment acts as an infinite heat reservoir, and no cost is associated with heat drawn from, or dumped into, the environment.
Elimination of the heat exchange with the environment, Q˙ 0, between the first and second laws (11.2, 11.3) yields an equation for power,
This equation is the generalization of (5.17) in Sec. 5.10 to include open system boundaries. The equation is valid for any system, open or closed, transient or steady state, that exchanges heat at least at T0, and possibly at other temperatures.
Note, that for Q˙ = Q˙ 0 = 0 there is nothing to be eliminated between the two equations, so that (11.4) is not relevant for fully adiabatic processes.
The factor T0 relates power loss to entropy generation; the lost power is sometimes denoted as irreversibility,
Equation (11.4) allows to relate irreversibility as measured by entropy generation S˙gen to power losses for complete thermodynamic systems, such as power and refrigeration cycles, in contact with the environment. Since S˙gen ≥ 0 and1 T0 > 0, this equation shows that irreversibilities reduce work output for a power producing system (where W˙ > 0, e.g., a power plant) or increase work demand for a power consuming system (where W˙ heat pump or a refrigerator).
The task of a thermal engineer can be described as to improve efficiency of a thermal system as much as possible. This requires to identify and reduce—as much as possible—causes of losses, i.e., irreversibilities. This will lead to a redesign of the system, which in turn leads to a change of the inflow, outflow and boundary conditions of the system.
A proper understanding of the losses associated with a system requires that all sources for irreversibility are considered. For a proper accounting of losses, the system boundary should be wide enough to include all causes for loss, so that internal and external irreversibilities are accounted for.
The redesign should start with removing the main causes for losses. If we indicate the different causes for entropy generation by Greek indices, we can write
The importance of the various entropy generating processes can be evaluated by a relative measure, e.g., the ratio between lost power and the total power exchange for the process
One will not be able to avoid losses altogether, and thus will have to accept values of a few percent (or more) for χα. Nevertheless, any reduction in irreversibilities that can be attained at reasonable cost for redesign and construction will lead to increased power production or decreased power consumption, and thus offer substantial savings in the long run of operation.