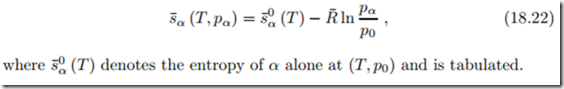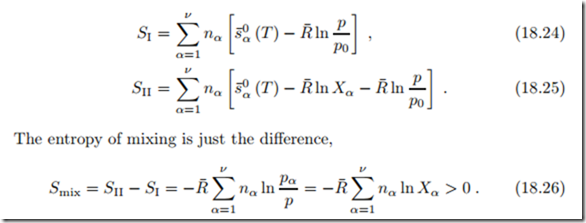Energy, Enthalpy and Specific Heats for Ideal Gases
For ideal gases, all energies and enthalpies depend only on the temperature T . The potential energy between particles is not relevant due to their large average distance, and thus there is no energy of mixing (Umix = 0), and no enthalpy of mixing, Hmix = Umix + pVmix = 0. With that, the energies and enthalpies of the components have the same temperature dependence in the mixture and in the pure state,
Entropy of Mixing for Ideal Gas
While volume, energy and enthalpy do not change when originally separated ideal gases at (T, p) (state I) are mixed, so that the mixture is at (T, p) (state II), the entropy does change. We compute the entropy for the two cases.
Component α fills the mixture volume V at temperature T and is at its partial pressure pα. Its entropy is not affected by the presence of other components, it reads just as for a single component,
With Xα = pα the molar entropy of one component in the mixture can be rewritten as
Accordingly, the entropy of component α depends only on the relative amount of α, while the composition of other components Xβ (β /= α) does not play a role.
In the unmixed state, all components are at (T, p) (i.e., Xα = 1), and in the mixed state the components are at (T, pα). The corresponding total entropies follow from summation over all components as
The entropy of mixing is positive, since Xα ≤ 1. Thus, entropy grows in mixing, and we conclude that mixing is an irreversible process, with a work loss. We shall later discuss how work could be obtained by reversible mixing.
The molar entropy of a mixture follows from (18.25) by division with the mole number n as