Application of Advanced Control Concepts in Active Power Control
Applying various types of renewable power plants with different characteristics will increase the complexity and number of state variable that should be control in a large-scale interconnected systems. Advanced control technology should be designed to address these types of necessity. On the other hand, in practical environment, one of the main observed problems in the control of AGC systems is the limitation to access and measurement of state variables. In order to solve this problem, an optimal output feedback method as an advanced LQR controller could be proposed. In the output feedback method, only the measurable state variables within each control area are required to use for feedback. But in order to improve dynamic performance and better design for this controller, concept of intelligent regulator is added to the LQ regulators and as a result the PSO-based LQ output feedback regulator and ICA-based LQ output feedback are proposed to calculate the global optimal gain matrix of controller intelligently [26, 27].
Design of Advanced LQR Control for LFC System
The design of optimal control systems is an important function of control engi- neering. The purpose of design is to realize a system with practical components that will provide the desired operating performance [28]. In this section, in order to improve the dynamic performance of system and for more accuracy and better design for conventional LQR controller, intelligent techniques are added to find the global optimal gain matrix.
Overview of Optimal Output Feedback
The power system model, which explained in previous sections, consists of a set of equations which describe models of generators, inertia, loads, RES units, and their associated controls. A linearized model of this system could usually obtained by a proper linearization around their operating point [4]. The generalized form of state space representation of power system could be as follows:
To obtain the output feedback gain K with minimizing the (42), these three coupled Eqs. (52), (53), and (54) must be solved simultaneously. The first two of these are Lyapunov equations and the third is an equation for the gain K.
If R is positive definite and is nonsingular, then (54) may be solved for K [28]:
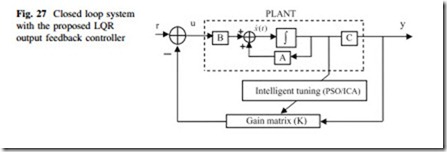
Various methods may be used to solve these equations, such as iterative methods [26]. But as shown in Fig. 27, the PSO and ICA algorithms are used to find the global optimal gain matrix.
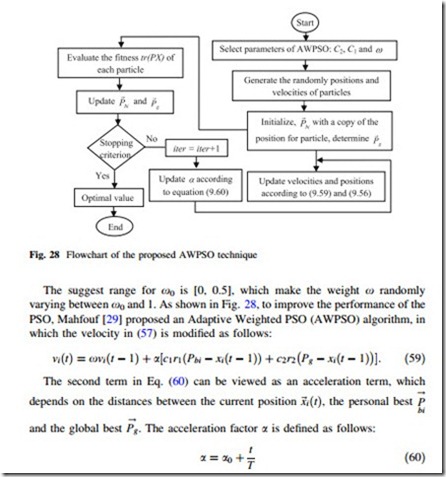
AWPSO Algorithm
PSO is a population-based heuristic search technique which imitates finding food principle of bird swarm [29]. A swarm consists of a set of particles where each particle represents a potential solution within the search space. Particles are then flown through the hyperspace, where the position of each particle is changed
where x is the inertia weight, c1 and c2 are positive constants and r1 and r2 are random numbers obtained from a uniform random distribution function in the interval [0, 1]. The parameters !P and !P represent the best previous position of the bi g i-th particle and position of the best particle among all particles in the population, respectively [29].
The inertia weight controls the influence of previous velocities on the new velocity. Large inertia weights cause larger exploration of the search space while smaller inertia weights focus the search on a smaller region. Typically, PSO started with a large inertia weight, which is decreased over time. But for more adaption, the following formula is used to change the inertia weight at each generation:
where x0 is the initial positive constant in the interval [0, 1] and r is random number obtained from a uniform random distribution function in the interval [0, 1].
where t is the current generation, T denotes the number of generations and the suggest range for a0 is [0.5, 1].
As can be seen from Eq. (59), the acceleration term will increase as the number of iterations increases, which will enhance the global search ability at the end of run and help the algorithm to jump out of the local optimum.
Imperialist Competitive Algorithm
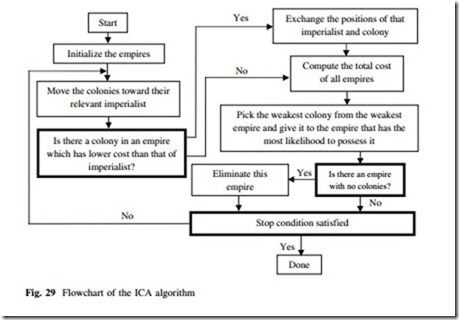
Imperialist competitive algorithm (ICA) is proposed by Caro Lucas et al. [30], and it is inspired by imperialist competition. ICA is a socio-politically motivated optimization algorithm which is similar to many other evolutionary algorithms, and starts with a random initial population or empires. Each individual agent of an empire is called country and the countries are categorized into two types; colony and imperialist state that collectively form empires. Imperialistic competitions among these empires form the basis of the ICA. During this competition, weak empires collapse and powerful ones take possession of their colonies. Imperialistic competitions converge to a state in which there exists only one empire and its colonies are in the same position and have the same cost as the imperialist [30].
With an N-dimensional optimization problem, a country is a 1 9 N array. This array is defined as follow is:
where b is assimilation factor, and r is a vector, and its elements are uniformly distributed random numbers in [0,1]. ximp; xold and xneware position of imperialist, old position of colony, new position of colony, respectively. For more information about deviation, refer to [30].
• Revolution of colonies: In this step, selected colonies of every imperialist are changed randomly, or revolved. Revolution is applied to a colony, with a probability of p.
• Exchange with best colony: If after assimilation and revolution steps, there are colonies which are better than their respective imperialists, the imperialist is exchanged with its best colony.
• Imperialist competition: Weakest imperialist among others, loses its weakest colony. One of other imperialists will capture the lost colony, randomly. An imperialist without colony will collapse.
As shown in Fig. 29, the mentioned steps are carried out, while stop conditions are not satisfied.
4.2 General Examples for Advanced Control Applications
The state space model for explained AGC models can be obtained to extract the required state matrices as shown in Fig. 27. By means of this advanced control techniques, it would be possible to analysis huge systems with several state variables just in matrix definitions. Then for better tuning intelligent methods will be applied. The proposed controllers are tested on two-area AGC power system, and a complete comparison between proposed output feedback controllers with AWPSO, with PSO, with Imperialist Competitive Algorithm (ICA) and
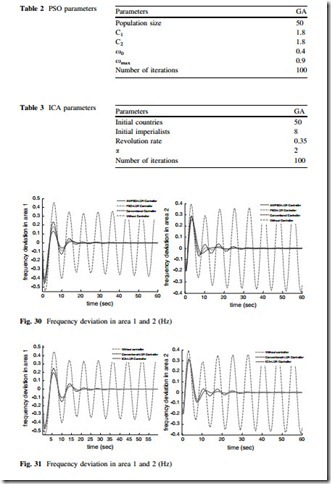
conventional output feedback controller are presented. In Tables 2 and 3, defined parameters for PSO and ICA algorithms are presented.
As shown in Figs. 30 and 31, using this method, the frequency deviation of each area and the tie-line power have a good dynamic response in comparing with conventional controller. Using the proposed intelligent methods, the frequency deviation of all areas is quickly driven back to zero and has a good dynamic response.