THE OUTPUT COEFFICIENT DESIGN CONCEPT

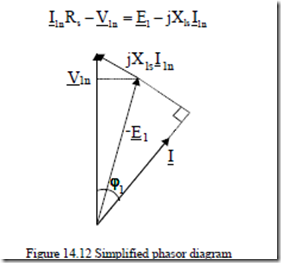
To calculate the relationship between the D_is²⋅L and the machine power and performance, we start by calculating the airgap apparent power S_g,

S_gap = 3E I_{1 1n} (14.6) where E₁ is the airgap emf per phase and I_1n rated current (RMS values). Based on the phasor diagram with zero stator resistance (R_s = 0), Figure 14.12.

I1nRs −V1n = −E1 jXls I1n

(14.7)

V1n

	Figure 14.12 Simplified phasor diagram
Or	KE = VE11n ≈ −1 xls ⋅sinϕ1	(14.8)
with	xls = X Ils 1n	(14.9)

V1n

The p.u. value of stator leakage reactance increases with pole pairs p₁ and so does sinϕ₁ (power factor decreases when p₁ increases).

K_E ≈ 0.98−0.005⋅p₁ (14.10)

Also, the input apparent power S_1n is

S1n = 3V I1n 1n = ηn cosPn ϕ1n (14.11)

where P_n is the rated output power and η_n and cosϕ_1n are the assigned values of rated efficiency and power factor based on past experience.

Typical values of efficiency have been given in Table 14.3 for Design B and E (NEMA). Each manufacturer has its own set of data.

Efficiency increases with power and decreases with the number of poles. Efficiency of wound rotor IMs is slightly larger than that of cage rotor IMs of same power and speed because the rotor windings are made of copper and the total additional load (stray) losses are lower.

As efficiency is defined with stray losses p_stray of 0.5 to1.0% of rated power in Europe (still!) and with the latter (p_stray) measured in direct load tests in the U.S.A., differences in actual losses (in IMs of same power and nameplate efficiency) of even more than 20% may be encountered when motors fabricated in Europe are compared with those made in the U.S.A.

Anyway, the assigned value of efficiency is only a starting point for design as iterations are performed until the best performance is obtained.

The power factor also increases with power and decreases with the number of pole pairs with values slightly smaller than corresponding efficiency for existing motors. More data on initial efficiency and power factor data will be given in subsequent chapters on design methodologies.

 

The emf E₁ may be written as a function of airgap pole flux φ,

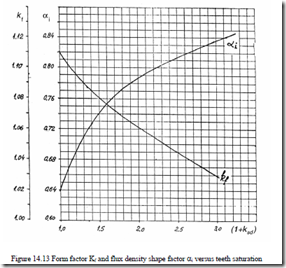
E₁ = 4f K WK_{1 f 1 w1}φ (14.12) where f₁ is frequency, 1.11 > K_f > 1.02 form factor (dependent on teeth saturation) (Figure 14.13), W₁ is turns per phase, and K_w1 is winding factor, φ pole flux.

φ = α τ_i LB_g (14.13) where α_i is flux density shape factor dependent on the magnetic saturation coefficient of teeth (Figure 14.13) and B_g is flux density in the airgap. The pole pitch τ is

τ = Dis ; n1 = f1 2p1 p1 Finally, Sgap is	(14.14)
Sgap = Kf αiKw1π2Dis2L 60n1 A B1 g with A1 the specific stator current load A1 (A/m),	(14.15)
A1 = 6πWI1 1n	(14.16)

π

Dis

We might separate the volume utilization factor C₀ (Esson’s constant) as

C0 = Kf αiKw1π2A B1 g = D602SLngap1 (14.17)

is

C₀ is not a constant as both the values of A₁(A/m) and airgap flux density (B_g) increase with machine torque and with the number of pole pairs.

The D_is²⋅L output coefficient may be calculated from (14.17) with S_gap from (14.6) and (14.11).

Dis2L = C1 60n ηnK PcosE nϕ1n (14.18)

0 1

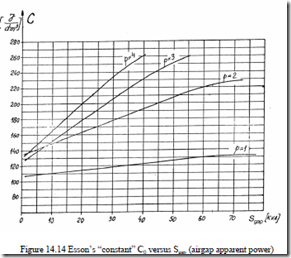
Typical values of C₀ as a function S_gap with pole pairs p₁ as parameter for low power IMs is given in Figure 14.14.

The D_is²⋅L (internal) output constant (proportional to rotor core volume) is, in fact, almost proportional to machine rated shaft torque. Torque production apparently requires less volume as the pole pairs number p₁ increases, C₀ increases with p₁ (Figure 14.14).

It is standard to assign a value λ to the stack length to pole pitch ratio

^{λ = L}_τ ^{= 2}_π^LpDis¹ ; 0.6 < λ < 3.0 (14.19)

The stator bore diameter may now be calculated from (14.18) with (14.19).

Dis = 3 2πλp1 C10 pf11 ηnK PcosE nϕ1n (14.20)

This is a standard design formula. However it does not say enough on the machine total volume (weight). Moreover, in many designs, the stator external (frame internal) diameters are standardized.

A similar (external) output coefficient D_is²⋅L may be derived if we first adopt a design current density J_con(A/m²) and consider the slot fill factor (with conductors), K_fill = 0.4 to 0.6, given together with the tooth and stator back iron flux densities B_ts and B_cs. With the airgap flux and tooth flux densities B_g and B_ts considered known, the stator slot height h_s is approximately

hs = BB_tsg6WIjcon1 Kn fill πD1 is = BBtsg jAcon1 Kfill (14.21)

Now the core radial height h_cs is

hcs = 2LBφ cs = α2i  π2Dp1is  BBcsg (14.22)

The outer stator diameter D_out is

D_out = D_is + ²(h_s + h_cs ) (14.23)

We may replace D_is from (14.23) in D_is²⋅L with h_s and h_cs from (14.21) and (14.22).

	Dis2L = Dout2L f⋅ 0(Dis )		(14.24)
And, finally,	f0(Dis )= 1+ (hs1+ hcs )2  2   Dis 		(14.25)
	f (D )= 1		(14.26)

_{0 is 2}

 + 2A B1 ts + αi π Bg 

	 jconKfillB Dg is 2 p1 Bcs 
From (14.24),	Dout2L = fD0(isD2Lis ) = C f0 01(Dis ) pf11 ηnK PcosE nϕ1n	(14.27)
As	π L = λ Dis 2p1	(14.28)

1

Dout = πλ2pC f10 12 ηnK PcosE ϕn 1n D fis 01(Dis ) (14.29)

Although (14.29) through the function [D f D_{is 0}( _is )]⁻¹ suggests that a minimum D_out may be obtained for given λ, B_g/B_co, B_g/B_t, j_con, and A₁, it seems to us more practical to use (14.29) to find the outer stator diameter D_out after the stator bore diameter was obtained from (14.20). Now if this value is not a standard one and a standard frame is a must, the aspect ratio λ is modified until D_out matches a standardized value.

The specific current loading A₁ depends on pole pitch τ and number of poles on D_is, once a certain cooling system (current density) is adopted. In general, it increases with D_is from values of less than 10³A/m for D_is = 4⋅10^-2m to 45,000 A/m for D_is = 0.4 m and 2p₁ = 2 poles. Smaller values are common for larger number of poles and same stator bore diameter.

On the other hand, the design current density j_con varies in the interval j_con = (3.5 – 8.0)⋅10⁶A/m² for axial or axial-radial air cooling. Higher values are designated to high speed IMs (lower pole pair numbers p₁) or for liquid cooling. While A₁ varies along such a large span and the slot height h_s to slot width b_s ratio is limited to K_aspect (3 – 6), to limit the slot leakage inductance, using A₁ may be avoided by calculating slot height h_s as h s = K aspect bs = K aspect πN is 1 − τbslott  = K aspect πNDsis 1 − BBtsg  (14.30)

D

s 

Higher values of aspect ratios are typical to larger motors.

This way, D_out²L is

Dout2L = C1 Pf1 ηnK PcosE nϕ1n 1+ 2KNaspects π 1− BBtsg + α2i pπ1 BBcsg 2 (14.31)

0 1

Also,

 DDout_is ≈ +1 2KNaspectπ 1− BBtsg + α2i pπ1 BBcsg (14.32)

s

To start, we may calculate D_is/D_out as a function of only pole pairs p₁ if B_g/B_ts = ct and B_g/B_cs = ct, with K_aspect and N_s (slots/stator) also assigned corresponding values (Table 14.4).

Table 14.4 Outer to inner stator diameter ratios

2p1	2	4	6	8	≥ 10
Dout Dis	1.65 – 1.69	1.46 – 1.49	1.37 – 1.40	1.27 – 1.30	1.24 – 1.26

The stack aspect ratio λ is assigned an initial value in a rather large interval: 0.6 to 3.

In general, longer stacks, allowing for a smaller stator bore diameter (for given torque) lead to shorter stator winding end connections, lower winding losses, and lower inertia, but the temperature rise along the stack length may become important. An optimal value of λ is highly dependent on IM design specifications and the objective function taken into consideration. There are applications with space shape constraints that prevent using a long motor.

Example 14.1 Output coefficient

Let us consider a 55 kW, 50 Hz, 400 V, 2p₁ = 4 induction motor whose assigned (initial) rated efficiency and power factor are η_n = 0.92, cosϕ_n = 0.92. Let us determine the stator internal and external diameters D_out and D_is for λ = L/τ = 1.5.

Solution

The emf coefficient K_E (14.10) is: K_E = 0.98 – 0.005⋅2 = 0.97 The airgap apparent power S_gap (14.3) is

Sgap = 3K VIE 1 1n = KE cosPϕ ηnn n VA

Esson’s constant C₀ is obtained from Figure 14.14 for p₁ = 2 and S_gap = 63.03⋅10³VA: C₀ = 222⋅10³J/m³.

For an airgap flux density B_g = 0.8T, K_w1 = 0.955, α_i = 0.74, K_f = 1.08 (teeth saturation coefficient 1 + K_st = 1.5, Figure 4.13). The specific current loading A₁ is (14.17).

A1 = K αiKCw10 π2Bg = 1.08⋅0.74222 10⋅0.⋅ 9553 ⋅0.8π2 = 36.876 10⋅ 3A/m

f

with λ = 1.5 from (14.20) stator internal diameter D_is is obtained.

D_is = ³ 2 1.5^{2 2}_⋅^{⋅ ⋅} 222 10¹_⋅ 3 ⋅ 50² ⋅ 63.03 10⋅ ³ = 0.2477m

The stack length L (14.19) is

L m

with j_con = 6⋅10⁶A/m, K_fill = 0.5, B_ts = B_cs = 1.6 T, the stator slot height h_s is (14.21).

h_s m

The back iron height h_cs (14.22) is

hcs = α π2i 2Dpis BBg = 0.742 2 2⋅π⋅⋅ ⋅0.2477 ⋅1.60.8 ≈ 36 10⋅ −3m

1 cs

The external stator diameter D_out becomes

D_out = D_is + 2(h_cs + h_s )= 0.2477+ 2 0.( 024584+0.036)= 0.3688m

With N_s = 48 slots/stator and a slot aspect ratio K_aspect = 3.03, the value of slot height h_s (14.30) is

hs = Kaspect πNDsis 1− BBtsg  = 3.03π 0.247748 1− 1.60.8 = 0.0246m

About the same value of h_s as above has been obtained. It is interesting to calculate the approximate value of the specific tangential force σ_tan.

σ_tan ≈

πD_is 2 _L ¹ 2 ⋅0.2917⋅0.2477

_

=1.246 10⋅ ⁴ N/m² =1.246N/cm²

This is not a high value and the slot aspect ratio K_aspect = h_s/b_s = 3.03 is a clear indication of this situation.

Apparently the machine stator internal diameter may be reduced by increasing A₁ (in fact, C₀ is Esson’s constant). For the same λ, the stack length will be reduced, while the stator external diameter will also be slightly reduced (the back iron height h_cs decreases and the slot height increases).

Given the simplicity of the above analytical approach further speculations on better (eventually optimized) designs are considered inappropriate here.

14.10 THE ROTOR TANGENTIAL STRESS DESIGN CONCEPT

The rotor tangential stress σ_tan(N/m²) may be calculated from the motor torque T_e.

σtan = (πD LTisen )2⋅Dis (N/m2 ) The electromagnetic torque Ten is approximately	(14.33)
 en ≈ p P 11 πn  (+−pPmecn ) T 	(14.34)

⋅

2 f 1 S1 n

P_n is the rated motor power; S_n = rated slip.

The rated slip is less than 2 to 3% for most induction motors and the mechanical losses are around 1% of rated power.

T_enP_n ^p_f1¹ (14.35)

Choosing σ_tan in the interval 0.2 to 5 N/cm² or 2,000 to 50,000 N/m², we may use (14.33) directly with ^{λ = 2}_π^{p L}D¹is to determine the internal stator diameter.

Dis = 3 π λσ24p1tan 0.1641⋅Pn ⋅ pf11  (14.36)

No apparent need occurs to adopt at this stage efficiency and power factor values for rated load.

We may now adopt the no-load value of airgap flux density B_g0,

µ03 2WK1 w1 0I (14.37)

Bg0 = πp K g 11 c ( + Ks )

where the no load current I₀ and the number of turns/phase are unknown and the airgap g, Carter’s coefficient K_c, and saturation factor K_s are assigned pertinent values.

gg≈≈(0.1(0.1++0.0.01202³³ PPn_n ))⋅⋅1010−−³3[ ][ ]m ; for pm ; for p11=≥12 (14.38)

Typical values of airgap are 0.35, 0.4, 0.45, 0.5, 0.55 … mm, etc. Also, K_c

≈ (1.15 – 1.35) for semiclosed slots and K_c = 1.5 – 1.7 for open stator slots (large power induction motors). The saturation factor is typically K_s = 0.3 – 0.5 for p₁ ≥ 2 and larger for 2p₁ = 2.

The airgap flux density B_g is

B_g = (0.5−0.7)T for 2p₁ = 2

BBg =₌(0.(0.765−₋0.0.875)T for )T for 22p1p1₌=64 (14.39)

g

B_g = (0.75−0.85)T for 2p₁ = 8

The larger values correspond to larger motors.

The product, W₁I₀, is thus obtained from (14.37). The number of turns W₁ may be calculated from the emf E₁ (14.12 and (14.13).

W1 = 4f K K1 Ef 1 w1φ = 4f K K1 f Ew11α π2pi 1D LBis g (14.40) with W₁I₀ and W₁ known, the no load (magnetization) current I₀ may be obtained. The airgap active power P_gap is

Pgap = Ten 2πf1 = 3K VIE 1 T (14.41) p₁

where I_T is the stator current torque component (in phase with E₁). With I_T determined from (14.41), we may now calculate the stator rated current I_1n.

I1n ≈ I02 + IT2 The rotor bar current (for a cage rotor) Ib is	(14.42)
Ib ≈ 2mWK1 w1 TI	(14.43)

Nr

N_r – number of rotor slots, m – number of stator phases.

We may now check the product η_ncosϕ_1n.

ηn cosϕ =n 3VIP1 1n n <1 (14.44)

The linear current loading A₁ may be also checked,

A1 = 2mWIπDis1 1n (14.45)

and eventually compared with data from existing similar motors.

With all these data available, the sizing of stator and rotor slots and their windings is feasible. Then the machine reactances and resistances and the steady-state performance may be calculated. Knowing the motor geometry and the loss breakdown, the thermal aspects (design) may be approached. Finally, if the temperature rise or other performance are not satisfactory, the design process is repeated.

Given the complexity of such an enterprise, some coherent methodologies are in order. They will be developed in subsequent chapters.

Example 14.2 Tangential stress

Let us consider the motor data of Example 14.1, adopt σ_tan = 1.5⋅10⁴N/m², and determine the values of D_is, L, W₁, I₀, I_1n, η_ncosϕ_n.

Solution

With p₁ = 2, P_n = 55 kW, f₁ = 50 Hz, λ = 1.5, from (14.36),

Dis = ₃ 4 2 0.⋅ ⋅_π21.5 1.51641 55 10_⋅ ⋅_⋅104⋅_⋅50³ ⋅2 = 0.2352m

The stack length L is

L m

with B_g = 0.8, K_f = 1.08, α_i = 0.74, K_w1 = 0.955, K_E = 0.97, and from (14.40), the number of turns per phase W₁ is

 ^400⋅ ⋅2 2

0.97⋅

W1 = 4⋅50⋅1.08⋅0.955⋅0.74⋅π⋅0.2352⋅0.277⋅0.8 = 36turns/phase

The rated electromagnetic torque T_en (14.35) is

T_en 0. _n Nm

Now, from (14.41), the torque current component I_T is

IT ₌ T_en ⋅ π2 f_{1 =} 361.02⋅ π2 50 ₌ 84.24A

The magnetization current I₀ is obtained from (14.37).

I0 = Bg0µπ03 2p K g 11 cWK(1 +w1Ks ) = 0.81.⋅π⋅ ⋅256 102 1.⋅ 25−6⋅⋅0.3655⋅0.⋅(1955+0.5⋅3 2)⋅10−3 = 28.36A

The airgap g (14.38) is

g ⁼ (0.1+0.012 55000 10³ )⋅ ⁻³ = 0.55 10⋅ ⁻³m

The stator rated current I_1n is

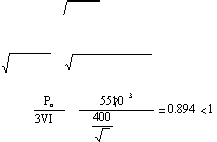I_1n = I₀² + I_T² = 28.36² +84.24² = 88.887A

η_n cosϕ_1n = =

^{1 1n} 3⋅ ⋅88.887

3

This corresponds to a rather high (say) η_n = cosϕ_1n = 0.9455.

Note that these values appear at design starting, before all the losses in the machine have been assessed. They provide a design start without Esson’s (output) constant which changed continuously over the last decade as material quality and cooling systems improved steadily.