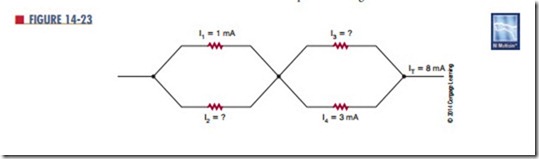
Kirchhoff’s Voltage law
Kirchhoff ’s second law is referred to as Kirchhoff’s voltage law, and it states the following:
● The algebraic sum of all the voltages around a closed circuit equals 0.
Here is another way of stating Kirchhoff ’s voltage law:
● The sum of all the voltage drops in a closed circuit equals the voltage source.
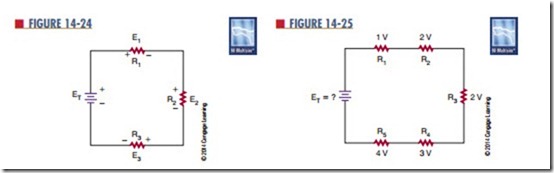
In Figure 14-24 there are three voltage drops and one voltage source (voltage rise) in the circuit. If the volt- ages are summed around the circuit as shown, they equal 0.
Notice that the voltage source (ET) has a sign oppo- site that of the voltage drops. Therefore the algebraic sum equals 0.
Looking at this another way, the sum of all the voltage drops equals the voltage source.
Both of the formulas shown are stating the same thing and are equivalent ways of expressing Kirchhoff ’s voltage law.
The key to remember is that the polarity of the voltage source in the circuit is opposite to that of the voltage drops.
Questions
1. State Kirchhoff’s voltage law in two different ways.
2. A series resistive circuit is connected to a 12-volt voltage source. What is the total voltage drop in the circuit?
3. A series circuit has two identical resistors connected in series with a 9-volt battery. What is the voltage drop across each resistor?
4. A series circuit is connected to a 12-volt voltage source with three resistors. One resistor drops
3 V and another resistor drops 5 V. What is the voltage drop across the third resistor?
5. refer to Figure 14-25. What is the total voltage applied to the circuit?