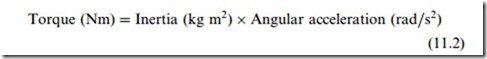LOAD REQUIREMENTS – TORQUE–SPEED CHARACTERISTICS
The most important things we need to know about the load are the steady-state torque–speed characteristic, and the effective inertia as seen by the motor. In addition, we clearly need to know what perform- ance is required. At one extreme, for example, in a steel-rolling mill, it may be necessary for the speed to be set at any value over a wide range, and for the mill to react very quickly when a new target speed is demanded. Having reached the set speed, it may be essential that it is held very precisely even when subjected to sudden load changes. At the other extreme, for example, a large ventilating fan, the range of set speed may be quite limited (perhaps from 80% to 100%); it may not be important to hold the set speed very precisely; and the time taken to change speeds, or to run-up from rest, are unlikely to be critical.
At full speed both of these examples may demand the same power, and at first sight might therefore be satisfied by the same drive system. But the ventilating fan is obviously an easier proposition, and it would be overkill to use the same system for both. The rolling mill would call for a regenerative d.c. or a.c. drive with tacho or encoder feedback, while the fan could quite happily manage with a cheaper open-loop inverter- fed induction motor drive, or even perhaps a simple voltage-controlled induction motor.
Although loads can vary enormously, it is customary to classify them into two major categories, referred to as ‘constant-torque’ or ‘fan or pump’ types. We will use the example of a constant-torque load to illustrate in detail what needs to be done to arrive at a specification for the torque–speed curve. An extensive treatment is warranted because this is often the stage at which users come unstuck.
Constant-torque load
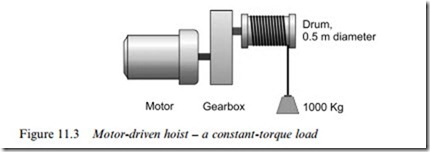
A constant torque load implies that the torque required to keep the load running is the same at all speeds. A good example is a drum-type hoist, where the torque required varies with the load on the hook, but not with the speed of hoisting. An example is shown in Figure 11.3.
The drum diameter is 0.5 m, so if the maximum load (including the cable) is say 1000 kg, the tension in the cable (mg) will be 9810 N, and the torque applied by the load at the drum will be given by force x radius ¼ 9810 x 0:25 � 2500 Nm. When the speed is constant (i.e. the load is not accelerating), the torque provided by the motor at
the drum must be equal and opposite to that exerted at the drum by the load. (The word ‘opposite’ in the last sentence is often omitted, it being understood that steady-state motor and load torque must necessarily act in opposition.)
Suppose that the hoisting speed is to be controllable at any value up to a maximum of 0.5 m/s, and that we want this to correspond with a maximum motor speed of around 1500 rev/min, which is a reasonable speed for a wide range of motors. A hoisting speed of 0.5 m/s corresponds to a drum speed of 19 rev/min, so a suitable gear ratio would be say 80:1, giving a maximum motor speed of 1520 rev/min.
The load torque, as seen at the motor side of the gearbox, will be reduced by a factor of 80, from 2500 to 31 Nm at the motor. We must also allow for friction in the gearbox, equivalent to perhaps 20% of the full-load torque, so the maximum motor torque required for hoisting will be 37 Nm, and this torque must be available at all speeds up to the maximum of 1520 rev/min.
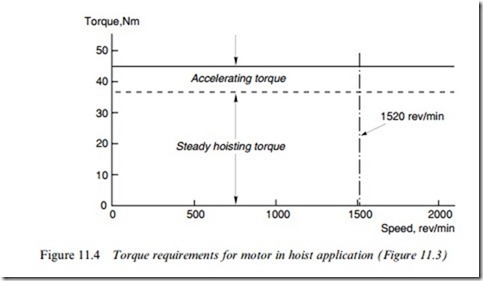
We can now draw the steady-state torque–speed curve of the load as seen by the motor, as shown in Figure 11.4.
The steady-state motor power is obtained from the product of torque (Nm) and angular velocity (rad/s). The maximum continuous motor power for hoisting is therefore given by
At this stage it is always a good idea to check that we would obtain roughly the same answer for the power by considering the work done per second at the load. The force (F ) on the load is 9810 N, the velocity
(v) is 0.5 m/s so the power (Fv) is 4.9 kW. This is 20% less than we obtained above, because here we have ignored the power lost in the gearbox.
So far we have established that we need a motor capable of continuously delivering 5.9 kW at 1520 rev/min in order to lift the heaviest load
at the maximum required speed. However, we have not yet addressed the question of how the load is accelerated from rest and brought up to the maximum speed. During the acceleration phase the motor must produce a torque greater than the load torque, or else the load will descend as soon as the brake is lifted. The greater the difference between the motor torque and the load torque, the higher the acceleration. Suppose we want the heaviest load to reach full speed from rest in say 1 s, and suppose we decide that the acceleration is to be constant. We can calculate the required accelerating torque from the equation of motion, i.e.
We usually find it best to work in terms of the variables as seen by the motor, and therefore we first need to find the effective total inertia as seen at the motor shaft, then calculate the motor acceleration, and finally use equation (11.2) to obtain the accelerating torque.
The effective inertia consists of the inertia of the motor itself, the referred inertia of the drum and gearbox, and the referred inertia of the load on the hook. The term ‘referred inertia’ means the apparent inertia, viewed from the motor side of the gearbox. If the gearbox has a ratio of n:1 (where n is greater than 1), an inertia of J on the low-speed side appears to be an inertia of J=n2 at the high-speed side. (This formula is the same as that for finding the referred impedance as seen at the primary of an ideal transformer, as discussed in Chapter 7.)
In this example the load actually moves in a straight line, so we need to ask what the effective inertia of the load is, as ‘seen’ at the drum. The geometry here is simple, and it is not difficult to see that as far as the inertia seen by the drum is concerned the load appears to be fixed to the surface of the drum. The load inertia at the drum is then obtained by using the formula for the inertia of a mass m located at radius r, i.e. J ¼ mr2, yielding the effective load inertia at the drum as 1000 kg x (0:25 m)2 ¼ 62:5 kg m2.
The effective inertia of the load as seen by the motor is 1=(80)2 x 62:5 � 0:01 kg m2. To this must be added firstly the motor inertia (which we can only estimate by consulting the manufacturer’s catalogue for a 5.9 kW, 1520 rev/min motor, which yields a figure of 0:02 kg m2), and secondly the referred inertia of the drum and gearbox, which again we have to look up. Suppose this yields a further 0:02 kg m2. The total effective inertia is thus 0:05 kg m2, of which 40% is due to the motor itself.
The acceleration is easy to obtain, since we know the motor speed is required to rise from 0 to 1520 rev/min in 1 s. The angular acceleration is given by the increase in speed divided by the time taken, i.e.
Hence in order to meet both the steady-state and dynamic torque requirements, a drive capable of delivering a torque of 45 Nm ( ¼ 37 þ 8) at all speeds up to 1520 rev/min is required, as indicated in Figure 11.4.
In the case of a hoist, the anticipated pattern of operation may not be known, but it is likely that the motor will spend most of its time hoisting rather than accelerating. Hence although the peak torque of 45 Nm must be available at all speeds, this will not be a continuous demand, and will probably be within the short-term overload capability of a drive which is continuously rated at 5.9 kW.
We should also consider what happens if it is necessary to lower the fully loaded hook. We allowed for friction of 20% of the load torque (31 Nm), so during descent we can expect the friction to exert a braking torque equivalent to 6.2 Nm. But in order to prevent the hook from running away, we will need a total torque of 31 Nm, so to restrain the load the motor will have to produce a torque of 24.8 Nm. We would naturally refer to this as a braking torque because it is necessary to prevent the load on the hook from running away, but in fact the torque remains in the same direction as when hoisting. The speed is however negative, and in terms of a ‘four-quadrant’ diagram (e.g. Figure 3.17) we have moved from quadrant 1 to quadrant 4, and thus the power flow is reversed and the motor is regenerating, the loss of potential energy of the descending load being converted back into electrical form. Hence, if we wish to cater for this situation we must go for a drive that is capable of continuous regeneration: such a drive would also have the facility for operating in quadrant 3 to produce negative torque to drive down the empty hook if its weight was insufficient to lower itself.
In this example the torque is dominated by the steady-state requirement, and the inertia-dependent accelerating torque is comparatively modest. Of course if we had specified that the load was to be accelerated in one-fifth of a second rather than 1 s, we would require an accelerating torque of 40 Nm rather than 8 Nm, and as far as torque requirements are concerned the acceleration torque would be more or less the same as the steady-state running torque. In this case it would be necessary to consult the drive manufacturer to determine the drive rating, which would depend on the frequency of the start–stop sequence.
The question of how to rate the motor when the loading is intermit- tent is explored more fully in Section 11.4.2, but it is worth noting that if the inertia is appreciable the stored rotational kinetic energy (1=2Jv2) may become very significant, especially when the drive is required to bring the load to rest. Any stored energy either has to be dissipated in the motor and drive itself, or returned to the supply. All motors are inherently capable of regenerating, so the arrangement whereby the kinetic energy is recovered and dumped as heat in a resistor within the drive enclosure is the cheaper option, but is only practicable when the energy to be absorbed is modest. If the stored kinetic energy is large, the drive must be capable of returning energy to the supply, and this inevitably pushes up the cost of the converter.
In the case of our hoist, the stored kinetic energy is only 1=2x 0:05 (1520 x 2p=60)2 ¼ 633 J, or about 1% of the energy needed to heat up a mug of water for a cup of coffee. Such modest energies could easily be absorbed by a resistor, but given that in this instance we are providing a regenerative drive, this energy would also be returned to the supply.
Inertia matching
There are some applications where the inertia dominates the torque requirement, and the question of selecting the right gearbox ratio has to be addressed. In this context the term ‘inertia matching’ often causes confusion, so it worth explaining what it means.
Suppose we have a motor with a given torque, and we want to drive an inertial load via a gearbox. As discussed previously, the gear ratio determines the effective inertia as ‘seen’ by the motor: a high step-down ratio (i.e. load speed much less than motor speed) leads to a very low referred inertia, and vice-versa.
If the specification calls for the acceleration of the load to be maximised, it turns out that the optimum gear ratio is that which causes the referred inertia of the load to be equal to the inertia of the motor. Applications in which load acceleration is important include all types of positioning drives, e.g. in machine tools and phototypesetting. (There is another electrical parallel here – to get the most power into a load from a source with internal resistance R, the load resistance must be made equal to R.)
It is important to note, however, that inertia matching only maximises the acceleration of the load. Frequently it turns out that some other aspect of the specification (e.g. the maximum required load speed) cannot be met if the gearing is chosen to satisfy the inertia matching criterion, and it then becomes necessary to accept reduced acceleration of the load in favour of higher speed.
Fan and pump loads
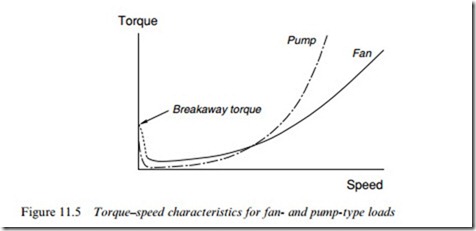
Fans and pumps have steady-state torque–speed characteristics which generally have the shapes shown in Figure 11.5.
These characteristics are often approximately represented by assuming that the torque required is proportional to the square or the cube of the speed, giving rise to the terms ‘square-law’ or ‘cube-law’ load. We should note, however, that the approximation is seldom valid at low speeds because most real fans or pumps have a significant static friction or breakaway torque (as shown in Figure 11.5), which must be overcome when starting.
When we consider the power–speed relationships the striking difference between the constant-torque and fan-type load is underlined. If the motor is rated for continuous operation at the full speed, it will be very lightly loaded (typically around 20%) at half speed, whereas with the constant torque load the power rating will be 50% at half speed.
Fan-type loads which require speed control can therefore be handled by drives which can only allow reduced power at such low speeds, such as the inverter-fed cage induction motor without additional cooling, or the voltage-controlled cage motor. If we assume that the rate of acceleration required is modest, the motor will require a torque–speed characteristic, which is just a little greater than the load torque at all speeds. This defines the operating region in the torque–speed plane, from which the drive can be selected.
Many fans do not require speed control of course, and are well served by mains-frequency induction motors. We looked at a typical example in Chapter 6, the run-up behaviour being contrasted with that of a constant-torque load in Figure 6.6.