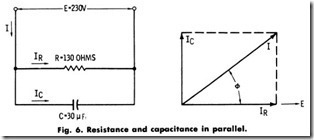
Problem-As shown in Fig. 6, a resistance of 130 ohms and a capacitance of 30 microfarads are connected in parallel across a 230-volt; 50 hertz supply. Find the following:
(a) Current in each circuit.
(b) Total current.
(c) Phase difference between the total current and the applied voltage.
(d) Power consumed.
(e) Power factor.
Solution-The capacitive reactance of the circuit is
(a) Current through the resistance is
Current through the capacitance is
(b) Total current is
(c) Phase difference is
(d) Power consumed is
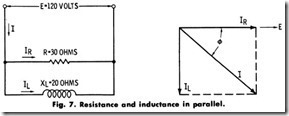
(e) Power factor according to (c) is 0.632, or 63.2%. Problem-Two circuits, Fig. 7, are connected inparallel as shown.
If the voltage of the source is 120, calculate the
(a) Phase displacement.
(b) Power factor of the circuit.
(c) Total current.
Solution-With reference to the vector diagram in Fig. 7, the current through the ohmic resistance is ![]()
Current through the inductive reactance is
(a) Phase displacement is
(b) Power factor is
(c) Total current is
Problem-Given two circuits (Fig. 8) in parallel, one branch con sisting of a resistance of 15 ohms and the other of an inductive reactance of 10 ohms. When the impressed voltage is 110, .find the
(a) Current through the ohmic resistance.
(b) Current through the inductive reactance.
(c) Line current.
(d) Power factor.
(e) Angle of lag of the line current.
Solution-With reference to the vector diagram in Fig. 8, the
(a) Current through the ohmic resistance is
(b) Current through the inductive reactance is
(c) Total line current (IT) is
(d) Power factor is
(e) Angle of lag of the line current is
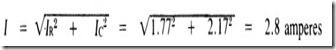


![Fig.-8.-Resistance-and-inductance-in[2] Fig.-8.-Resistance-and-inductance-in[2]](http://machineryequipmentonline.com/electric-equipment/wp-content/uploads/2020/06/Fig.-8.-Resistance-and-inductance-in2_thumb.jpg)