The Tempered Scale
The equal tempered musical scale is composed of 12 equally spaced intervals separated by a factor of 12 2 . All notes on the musical scale (excluding sharps and flats), however, are not equally spaced. This is because there are two one-half step intervals on the scale: that between E and F and that between B and C. The 12 tones, therefore, go as follow: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C (see Table 2.10).
Measuring Distortion
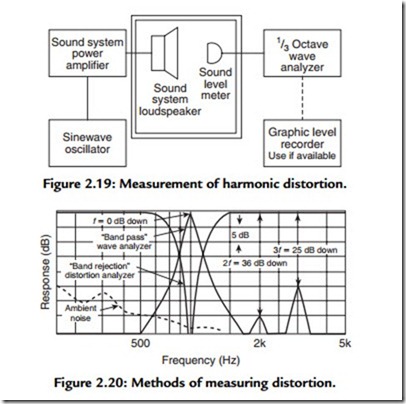
Figure 2.19 illustrates one of the ways of measuring harmonic distortion. Two main methods are employed. One uses a band rejection filter of narrow bandwidth having a rejection capability of at least 80 dB in the center of the notch. This deep notch “rejects” the fundamental of the test signal (usually a known-quality sine wave from a test audio oscillator) and permits reading the noise voltage of everything remaining in the rest of the bandpass. Unfortunately, this also includes the hum and noise, as well as the harmonic content of the equipment being tested (see Figure 2.20).
The second method is more useful. It uses a tunable wave analyzer. This instrument allows measurement of the amplitudes of the fundamental and each harmonic, as well as identifying the hum, the amplitude, and the noise spectrum shape (Figure 2.20). Such analyzers come in many different bandwidths, with a 1/10 octave unit allowing readings down to 1% of the fundamental (it is -45 dB at 2f ). By looking at Figure 2.20, it is easy to see that harmonic distortion appears as a spurious noise. Today, tracking filter wave analysis allows nonlinear distortion behavior to be “tracked” or measured.