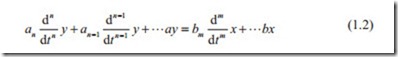Linear System
In any system, if there exists a linear relationship between two variables, then it is said that it is a linear system.
For example, the equation
represents a linear system. It means that if K is constant then the relationship (1.1) represents a linear relationship between two variables y and x. In general, any gov- erning differential equations between two variables x and y in the form of
is linear, where n and m represent the order of differential equations, and an, bm are constants. For real system n > m, any other form of equations that is not similar to Eq. (1.2) is called nonlinear system.
There are extensive theories that deal with linear systems, but the theories on nonlinear systems are very complex and little.
Example 1 The circuit diagram of equivalent DC servo motors is shown in Fig. 1.1.
The governing differential equation may be written as
where Vi, I, ωm are the input voltage, current, and angular speed. R and L are the resistance and inductance, respectively. This represents a linear system, where ωm is the output variable and Vi represents the input voltage.
For DC servo motor, we can write
R. Firoozian, Servo Motors and Industrial Control Theory, Mechanical Engineering Series, 1
Equation (1.6) now represents a linear differential system, and in control terminol- ogy, Vi is called the input variable and ωm is called the output variable. The Eq. (1.6) can be solved for ωm in terms of the input variable. In deriving Eq. (1.6), we ignore the external torque acting on the motor. If we consider the external torque, the gov- erning differential equation would have two input variables and one output variable.
For linear systems, the principle of superposition holds. It means that if input x1 causes output y1 and input x2 causes output y2, then input x1 + x2 causes output y1 + y2. This is a powerful principle, and we will use it throughout this book.