Frequency Response
For harmonic input in the form of x( t) = A sin ωt, the output for linear system will be in the form of y( t) = B sin( ωt − Ψ). The phase angle Ψ, and amplitude ratio M = B / A can be obtained from the transfer function. If s is replaced by iω, then the amplitude ratio and phase angle can be obtained from the resulting complex number in the following manner
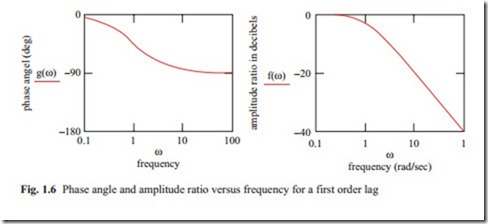
It is a common practice to plot the amplitude ratio in decibel and phase angle in degrees against frequency changing from zero to infinity. The frequency response is usually plotted in db and log of frequency. These diagrams for the first order trans- fer function are shown in Fig. 1.6.
The important points are at
w =1/t where the amplitude ratio is M = 0.707,
M = − 3 db (in decibels; i.e. 20 log(m)) and Φ: = − 45°. This frequency is known as the break frequency.
It can be seen from the frequency response curve and Eq. (1.32) that at low frequency, that is, at frequency much lower than w « 1/ t , the amplitude ratio is ap- proximately 0 db, and at frequency much higher than w » 1/ t , the amplitude ratio becomes a line with slope of 20 db/decade. These two lines are the asymptotes of the
frequency responses. For some mechanical systems, where the response is very slow, the frequency response may be plotted on octave scale instead of logarithmic scale.
Therefore, by knowing the time constant τ, the frequency response and the time response are completely known.