DC Servo Motors in Open and Closed Loop Velocity Control
First, the velocity control will be studied. The voltage equation of the DC motor ignoring the Inductance can be written as
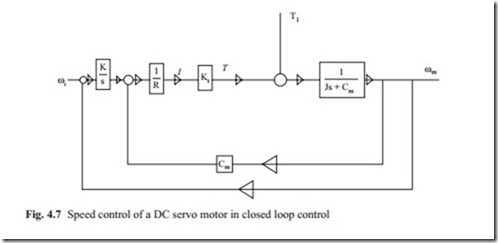
It can be seen that the dynamic characteristic of the motor is a first order transfer function (Fig. 4.7). This kind of transfer function was studied in previous chapters. The time constant increases when the inertia of motor is increased. The readers are encouraged to do the algebraic manipulation to find that the obtained transfer function is correct. When the external torque is applied, the speed drops according to the speed torque characteristic of the motor with a dynamic response according the transfer function given above. When it is required to have a constant speed, the external velocity feedback must be used. If a steady state error can be tolerated, a proportional controller may be used. For application where zero steady state is required, an integrator must be used.
To illustrate the procedure for studying such application, a velocity feedback with an integrator will be studied.
It can be seen that there is an internal velocity feedback. This helps to increase the damping of the system. A sensor such as a dc tacho may be used to measure the
velocity and then it is fed back to the integrator controller. The demand velocity is compared with the feedback velocity, which generates a voltage. The power unit, which amplifies the low level signal to large voltage and current, are not shown in the diagram. It must be clear that all feedbacks are negative. This is not shown in the diagram.
It can be seen that there are two input variables and one output variable. All parameters are given by manufacturer and the damping ratio C must be predicted experimentally and if it is very small can be set to zero. The gain of the integrator must be designed as to achieve maximum speed with acceptable damping in the system. Then the effect of external torque must be studied.
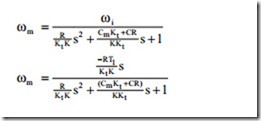
The overall transfer function can be obtained either from the governing differential equations or from the block diagram. The principle of superposition may be used to obtain the transfer function. First, the external torque is set to zero and the block diagram can be reduced to a single block. The command signal is then set to zero to obtain the transfer function, which relates the output velocity to the external torque. After some algebraic manipulation, the overall transfer function becomes
It can be seen that at steady state setting s to zero, the velocity is equal to the de- mand signal. When the torque is applied, the portion of the velocity which effects the speed is zero meaning that regardless of the external torque at steady state the velocity is constant. Both the relationship of the command signal and output veloc- ity and output torque and the command signal are governed by a second order char-
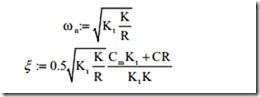
acteristic equation. The behavior of this kind of characteristic equation is governed by a natural frequency and a damping ratio.
The readers are encouraged to derive the above transfer functions by both meth- od of block diagram reduction using the principle of superposition and directly from the governing differential equations to find that the above calculations are correct. The characteristic equation as discussed in the previous chapters gives the natural frequency and damping ratio as
It can be seen that as K is increased, the speed of response increases and the damping ratio reduces. The designer has to make a compromise between speed of response and the damping ratio.
In the above example, only an integral control was used, the readers are encour- aged to study the effect of adding a proportional controller to the integral control. The block diagram of the control unit becomes (Fig. 4.8)
In this example, there are two parameters to adjust and a better performance can be achieved. The readers are encouraged to do the analysis and find the over- all transfer function. It is recommended that readers obtain a catalogue from the manufacturers of DC servo motors and to study the above analysis numerically. After adjusting the gains using state variable technology find the transient response numerically. MathCAD or other software may be used to do the analysis. Although the roots of the characteristic equation by adjusting the two control parameters, there are practical limitations such as amplifier saturation and power unit can only produce a maximum torque designed by manufacturer. These nonlinearities might produce instability. In practice, the theoretical analysis is only guidance what kind of performance can be achieved.
If a gearbox is used to reduce the speed of motor, the referred inertia to the motor should be added to the motor inertia. If the input to the output speed ratio is N, the referred inertia to the motor may be shown to be as Jl /N . The readers are encouraged to prove this.