Armature reaction and commutation:Armature Reaction

Armature Reaction

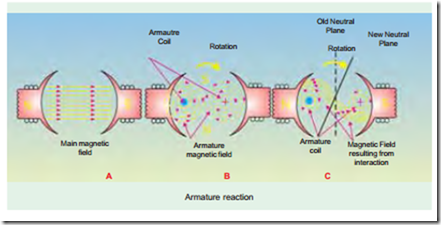
By armature reaction is meant the effect of magnetic field set up by armature current on the distribution of flux under main poles of a generator. The armature magnetic field has two effects :

(i) It demagnetises or weakens the main flux and

(ii) It cross-magnetises or distorts it.

The first effect leads to reduced generated voltage and the second to the sparking at the brushes.

which shows the flux distribution of a bi- polar generator when there is no current in the armature conductors. For convenience, only two poles have been considered, though the following remarks apply to multipolar fields as well. Moreover, the brushes are shown touching the armature conductors directly, although in practice, they touch commutator segments, It is seen that

(a) the flux is distributed symmetrically with respect to the polar axis, which is the line joining the centres of NS poles.

(b) The magnetic neutral axis or plane (M.N.A.) coincides with the geometrical neutral axis or plane (G.N.A.)

Magnetic neutral axis may be defined as the axis along which no e.m.f. is produced in the armature conductors because they then move parallel to the lines of flux.

Or M.N.A. is the axis which is perpendicular to the flux passing through the armature.

As hinted in Art. 27.2, brushes are always placed along M.N.A. Hence, M.N.A. is also called ‘axis of commutation’ because reversal of current in armature conductors takes place across this axis.

In Fig. 27.1 is shown vector OFm which rep- resents, both in magnitude and direction, the m.m.f. producing the main flux and also M.N.A. which is perpendicular to OFm.

In Fig. 27.2 is shown the field (or flux) set up by the armature conductors alone when carrying current, the field coils being unexcited. The direction of the armature current is the same as it would actually be when the generator is loaded. It may even be found by applying Fleming’s Right-hand Rule. The current direction is downwards in conductors under N-pole and upwards in those under S–pole. The downward flow is represented by crosses and upward flow by dots.

As shown in Fig. 27.2, the m.m.fs. of the armature conductors combine to send flux downwards through the armature. The direction of the lines of force can be found by applying cork-screw rule. The armature m.m.f. (depending on the strength of the armature current) is shown separately both in magnitude and direction by the vector OFA which is parallel to the brush axis.

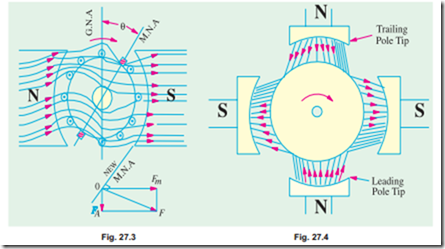
So far, we considered the main m.m.f. and armature m.m.f. separately as if they existed independently, which is not the case in practice. Under actual load conditions, the two exist simultaneously in the generator as shown in Fig. 27.3.

It is seen that the flux through the armature is no longer uniform and symmetrical about the pole axis, rather it has been distorted. The flux is seen to be crowded at the trailing pole tips but weakened or thinned out at the leading pole tips (the pole tip which is first met during rotation by armature conductors is known as the leading pole tip and the other as trailing pole tip). The strengthening and weakening of flux is separately shown for a four-pole machine in Fig. 27.4. As seen, air-gap flux density under one pole half is greater than that under the other pole half.

If Fig. 27.3 is shown the resultant m.m.f. OF which is found by vectorially combining OFm and OFA.

The new position of M.N.A., which is always perpendicular to the resultant m.m.f. vector OF, is also shown in the figure. With the shift of M.N.A., say through an angle q, brushes are also shifted so as to lie along the new position of M.N.A. Due to this brush shift (or forward lead), the armature conductors and hence armature current is redistributed. Some armature conductors which were earlier

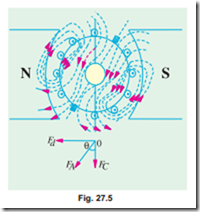
under the influence of N–pole come under the influence of S–pole and vice-versa. This regrouping is shown in Fig. 27.5, which also shows the flux due to armature conductors. Incidentally, brush position shifts in the same direction as the direction of armature rotation.

All conductors to the left of new position of M.N.A. but between the two brushes, carry current downwards and those to the right carry current upwards. The armature m.m.f. is found to lie in the direction of the new position of M.N.A. (or brush axis). The armature m.m.f. is now represented by the vector OFA which is not ver- tical (as in Fig 27.2) but is inclined by an angle q to the left. It can now be resolved into two rectangular components, OFd parallel to polar axis and OFC perpendicular to this axis. We find that

(i) component OFC is at right angles to the vector OFm (of Fig. 27.1) representing the main m.m.f. It produces distortion in the main field and is hence called the cross-magnetising or distorting component of the armature reaction.

(ii) The component OFd is in direct opposition of OFm which represents the main m.m.f. It exerts a demagnetising influence on the main pole flux. Hence, it is called the demagnetising or weakening component of the armature reaction.

It should be noted that both distorting and demagnetising effects will increase with increase in the armature current.

Crankshaft and Bearings part2

PC Hardware Interfaces: A Developer's Reference - Serial Buses—USB and FireWire

Engine Valve System part5

D.C.GENERATORS:Practical Generator

STEADY STATE EQUIVALENT CIRCUIT AND PERFORMANCE

Objective tests on transformer

The Capacitor-Start Motor

Power and Energy:Work and Force

Operation of the DC Welder Generator

Troubleshooting and Repairing Computer Printers - A modern printer

summary of Optoelectric Devices