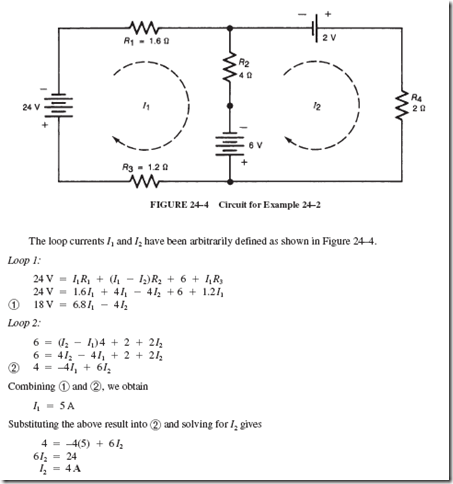
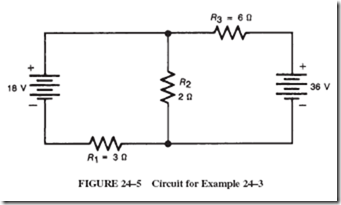
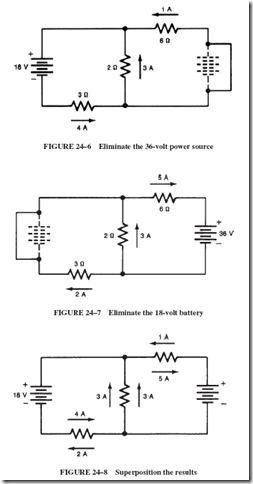
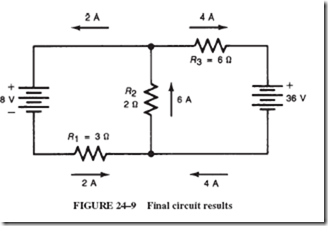
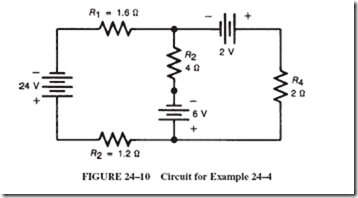
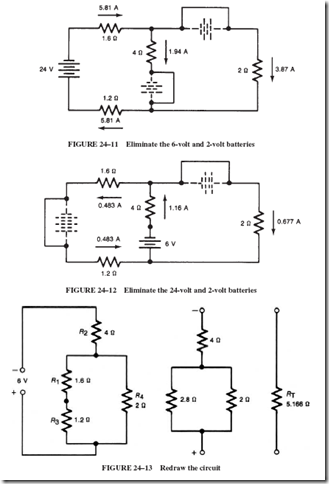
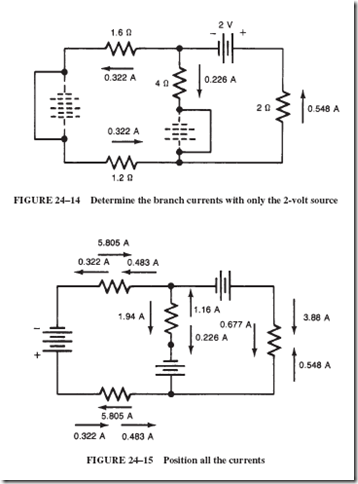
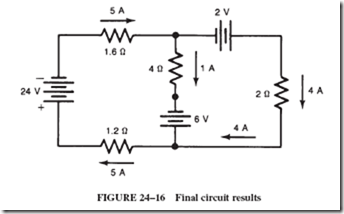
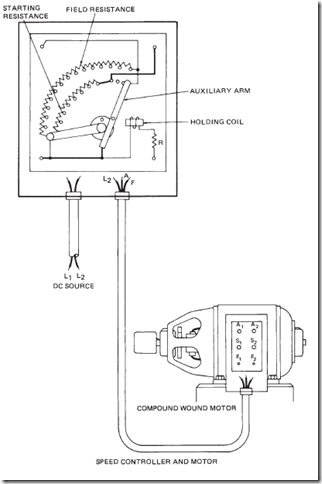
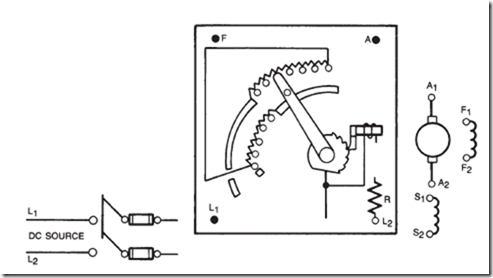
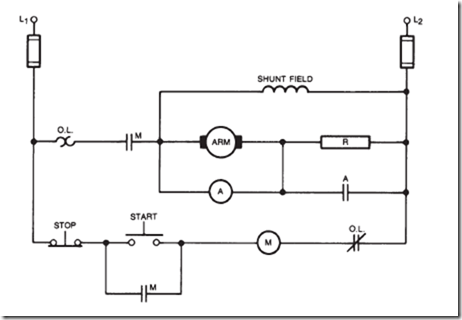
ALTERNATING-VOLTAGE GENERATION
A simple alternating-voltage generator consisting of a single coil rotating in a uniform magnetic field is shown in Figure 1–11.
The use of Fleming’s generator rule shows that an alternating voltage is generated in the coil as it rotates. If the ends of the coil are connected to two slip rings, the alternating voltage can be observed on an oscilloscope. This voltage pattern is a typical sine wave, as shown in Figure 1–12.
The generated voltage in an armature conductor is expressed by the formula
is the generated voltage in the armature conductor in volts, B is the generated magnetic flux of the field, L is the length of the armature conductor in inches, v is the velocity of rotation of the coil in inches per second, and 108 represents 100,000,000 lines of force that must be cut per second to cause one volt to be induced.
One of the magnetic measurements in the English system is the weber. One weber rep- resents an amount of magnetic flux equal to 100,000,000 lines. Therefore, it can be stated that voltage is induced at a rate of one weber per second (1/Wb/s). The amount of voltage induced in a conductor is proportional to three factors:
1. The strength of the magnetic field (flux density)
2. The length of the conductor (often expressed as the number of turns of wire)
3. The speed of the cutting action
Most ac generators have stationary coil windings and rotating field windings. How- ever, in Figure 1–11, the coil rotates and the field is stationary. In either case, the induced voltage in the coil windings depends upon the number of lines of force cut per second.
Development of an AC Sine Wave
To illustrate the development of the alternating-voltage sine-wave pattern shown in Figure 1–12, a more convenient form of the simple ac generator is needed.
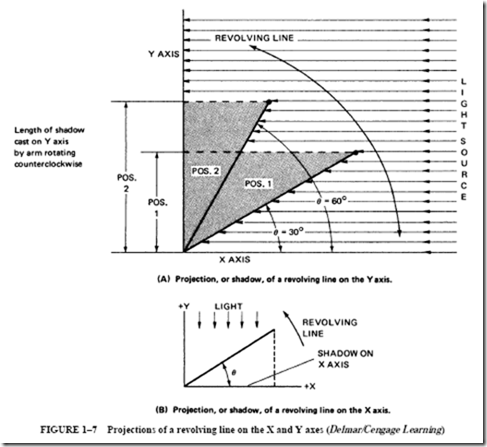
A simple ac generator is shown in Figure 1–13. The conductors of the coil are moving parallel to the lines of force. At this instant, almost no lines of force are being cut and the generated voltage is zero.
In Figure 1–14 the conductors of the coil have moved counterclockwise to a point 30° from the starting position. The conductors of the coil are now cutting across the field flux. As a result, a voltage is induced in the coil. The instantaneous voltage in this position is determined by
vinstantaneous = Vmaximum X sin L
Assuming that the maximum voltage is 141.4 V, the induced voltage at 30° is vi = Vmax X sin 30° = 141.4 X 0.5000 = 70.7 V
Movement across a Magnetic Field. By examining the triangle in Figure 1–14, it can be seen that the total velocity of the conductor (V ) has two components. There is a useless vertical component (v ) parallel to the magnetic lines of force. The other component (v ) p c is a useful horizontal component that crosses, or is perpendicular to, the magnetic lines of
force. Because voltage is generated only by the movement that cuts the magnetic field, the right triangle is solved for the v component:
vc = VT X sin 30°
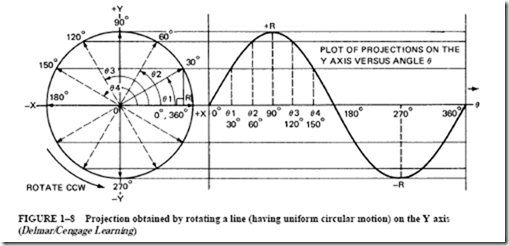
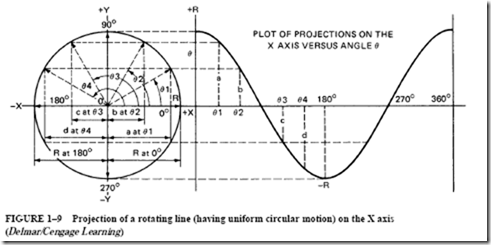
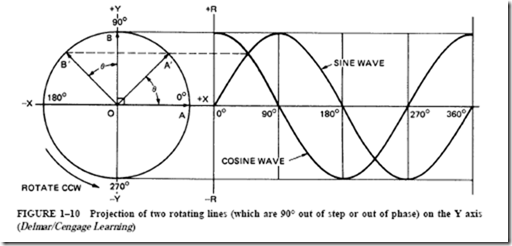
Note the similarity between the equations expressing velocity, voltage, and projections on the Y axis:
• Equation 1 was derived from a coil revolving in a magnetic field where the velocity components are resolved perpendicular to the magnetic field.
• Equation 2 was derived from a coil revolving in a magnetic field where the maximum voltage components are resolved into instantaneous voltage.
• Equation 3 was derived from rotating a line counterclockwise and taking the magnitude of its projection on the Y axis. In other words, R is resolved into its Y shadow.
The values vc , v, and y in equations 1 through 3 are called instantaneous values of the sine wave. VT , Vmax , and R are called the maximum values of the sine wave. The general forms of a voltage sine wave and a current sine wave are
The coil at 45°. In Figure 1–15 the coil is at a new position 45° from the starting position. Refer to the right triangle construction in the figure. The component of the angular velocity has increased slightly (as compared to Figure 1–14). There is a proportional increase in the induced voltage to an instantaneous value determined as follows:
The coil at 90°. In Figure 1–16 the coil has rotated to an angle of 90° from the starting position. The sine of 90° is 1.0; therefore, the generated voltage has a maximum value of 141.4 V. The conductors of the coil are perpendicular to the flux field. Because the greatest number of lines of flux are cut in a given time period in this position, the induced voltage must be a maximum value. As the armature coil continues to rotate counterclockwise, the direction and the instantaneous value of voltage can be deter- mined for any angle through 360° (one complete revolution). The resulting waveform is a sine wave of voltage. For each angular position of the coil in the magnetic field, the direction of the generated voltage can be obtained by Fleming’s generator rule. The value of the instantaneous voltage generated in the coil for each angular position can be found from the sine of the angle times Vmax .
During the design and construction of ac generators, an attempt is made to ensure a nearly perfect sine-wave voltage output. Motors, transformers, and other electrical equipment have better operating characteristics when they receive electrical energy from such ac generators.
Defining Alternating Voltage and Current
Alternating voltage may be defined as an electromotive force that changes continuously with time. It rises from zero to a maximum value in one direction and decreases back to zero. It then rises to the same maximum value in the opposite direction and again decreases to zero. These values are repeated again and again at equal intervals of time.
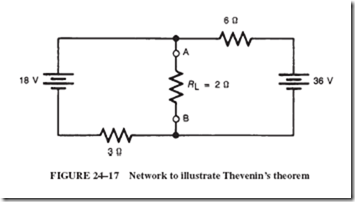
The alternator shown in Figure 1–11 is connected to a resistor, which is the external load. The alternating voltage of this generator causes an alternating current to be supplied to the load. As the alternating voltage varies in magnitude and direction, the current (in amperes) varies proportionally. Alternating current may be defined in a manner that is similar to the definition of alternating voltage. Refer to Figure 1–17.
Alternating current is a current that changes continuously with time. It rises from zero to a maximum value in one direction and decreases back to zero. It then rises to the same maximum value in the opposite direction and again decreases to zero. These values are repeated again and again at equal intervals of time.
FREQUENCY
The number of complete events or cycles per second is the frequency, measured in hertz. Sixty cycles per second equals 60 hertz, or 60 Hz.
In the United States and Canada, 60 Hz is used almost exclusively, with the exception of a few areas that use 25-Hz service. The advantage to using a higher-frequency service is that less iron and copper are required in the transformers. Therefore, they are lighter and lower in cost. Also, incandescent lamps operating at 60 Hz have no noticeable flicker. At 25 Hz, the flicker of incandescent lamps can be annoying.
The speed of a generator and the number of poles determine the frequency of the generated voltage. If a generator has two poles (north and south), and the coils rotate at a speed
of one revolution per second, the frequency is one cycle per second. If the generator has two pairs of poles, then a cycle is generated every half-revolution, or 2 hertz per second (2 Hz/s).
Frequency of an AC Generator
In the simple alternator, one cycle of voltage is produced each time the coil makes one revolution between the two poles. If this coil makes 60 revolutions per second, the alternating voltage generated will have a frequency of 60 cycles per second (60 Hz). The frequency of an ac generator is expressed by the following formula
Because there may be some confusion in using pairs of poles in the frequency formula, it is common practice to use the total number of poles of the alternator. In this case, the time constant of 60 s is doubled. For example, if a four-pole alternator turns at 1800 r/min, the frequency of the voltage output of the machine is
ELECTRICAL TIME DEGREES AND MECHANICAL DEGREES
When a coil makes one revolution in a generator with two poles, one cycle of voltage is generated. However, when a coil makes one revolution in a generator with four poles (Figure 1–18), two cycles of voltage are generated. Thus, a distinction must be made between mechanical and electrical degrees.
When a coil or armature conductor makes one complete revolution, it passes through 360 mechanical degrees.
When an electromotive force or an alternating current passes through one cycle, it passes through 360 electrical time degrees.
As the number of poles in an ac generator increases, the actual required driven speed in r/min decreases proportionally for a given frequency. The relationship between speed, number of poles, and frequency is shown in Table 1–1. The frequency values may be checked using the following frequency equation:
f = P X S + 120
The values for the number of poles and the speed in r/min may be substituted in the formula for each frequency value.
Alternating-voltage waveforms are not all sine waves. For example, a square-wave output or a rectangular output can be generated by electronic equipment, such as a signal generator. One type of electronic oscillator has a voltage output pattern that resembles a sawtooth (Figure 1–19).
For electrical energy transmitted at frequencies of 60 Hz and 25 Hz, the voltage wave pattern may be distorted so that it is not a true sine wave. Such distortion is due to conditions that may exist in ac generators, transformers, and other equipment. A distorted wave pattern consists of a fundamental wave (which is the frequency of the circuit) and other waves having higher frequencies. These waves are called harmonics and are superimposed on the fundamental wave. The exact appearance of the distorted wave will depend on the frequencies, magnitudes, and phase relationships of the voltage waves superimposed on the fundamental wave. For example, assume that a harmonic wave having a frequency three times that of the fundamental wave is superimposed on the fundamental wave (Figure 1–20). The resulting distorted wave pattern depends on the phase relationship between the harmonic wave and the fundamental wave.
In Figure 1–20 the harmonic wave is shown referred to the zero axis. It has a frequency three times that of the fundamental and is superimposed on the fundamen- tal wave. Note that the resultant pattern of the fundamental wave is different in the two diagrams. The difference arises because the phase relationship of the harmonic wave with the fundamental wave in the two illustrations is different.
This text cannot cover the various circuit problems involving unique ac voltage wave patterns. Therefore, it will be assumed that sine-wave voltage and current values are used throughout this text, unless otherwise noted.
HIGHER FREQUENCIES
It was noted earlier that the most common frequency used for the transmission of electrical energy is 60 Hz. Another value commonly used in aircraft and in other mobile equipment is 400 Hz.
In electronics, the frequencies used cover a very wide range. For example, audio frequencies between 20 and 16,000 Hz are used to operate speakers in amplifier units and radio receivers. Transmitted frequencies above 15,000 Hz are called radio frequencies. These higher frequencies are expressed in units of kilohertz (1 kHz = 1000 Hz), megahertz (1 MHz = 1,000,000 Hz or 1000 kHz), and gigahertz (1 GHz = 1,000,000,000 Hz or 1000 MHz).
SUMMARY
• Alternating current is more commonly used, but there are a number of applications where direct-current systems must be used or will do the job more efficiently than ac.
• AC alternators operate economically at relatively high voltages and heavy current ratings. DC generators are limited in both high voltages and large current ratings.
• The generation of large amounts of ac energy in large central stations is a more efficient and economical operation than in smaller local units.
• AC electrical energy can be transmitted at very high voltages over long distances (lowering I2R losses). Transformers raise or lower voltages as needed at generating stations or distribution points. Transformers cannot be used on dc systems.
• The ac induction motor is simple and rugged in construction. It has excellent operating characteristics and is far more economical in initial costs, replacement, and maintenance than are dc motors.
• The sine wave is the function of the position of a coil in a magnetic field.
• The cosine wave has the same pattern as the sine wave, but reaches its maximum value 90° before the sine wave.
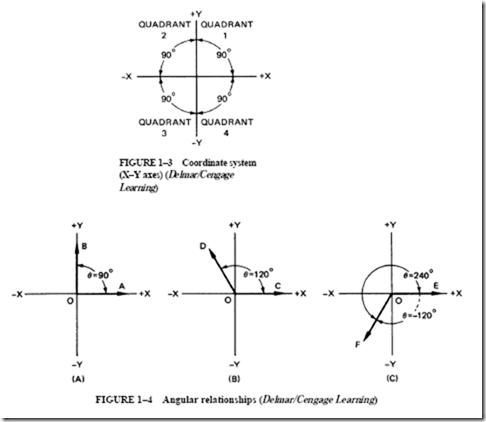
• Quadrants in a coordinate system are numbered counterclockwise.
• Angles are measured from the positive X axis to the indicated line in the counterclock- wise direction.
• Angles measured in the clockwise direction from the positive X axis to the indicated line are negative because the direction of measurement has changed.
• The formula for the induced voltage in an armature conductor is
•The induced voltage is directly proportional to the velocity component, V = vc /(sin L8), which is perpendicular to the magnetic field.
• The instantaneous value of alternating voltage is given by
• Alternating voltage is a voltage that changes continuously with time. It rises from zero to a maximum value in one direction, decreases to zero, rises to the same maximum value in the opposite direction, again decreases to zero, and then repeats these values at equal intervals of time.
• Alternating current is a current that changes continuously with time. It rises from zero to a maximum value in one direction, decreases to zero, rises to the same maximum value in the opposite direction, again decreases to zero, and then repeats these values at equal intervals of time.
• A cycle of alternating voltage or alternating current can be defined as that voltage or current that rises from zero to a positive maximum value, returns to zero, then rises to a negative maximum value, again returns to zero, and repeats these values at equal intervals of time.
• Frequency is the number of complete events or cycles per second (Hz) of alternating voltage or alternating current.
• Each cycle is divided into two alternations, with each alternation equal to 180 electrical time degrees.
• The relationship between the number of poles, speed, and frequency is expressed by
• As the number of poles in an ac generator increases, the actual required driven speed in r/min decreases proportionally for a given frequency.
• When using a higher frequency, less iron and copper are required in transformers, motors, and other electrical equipment.
• Alternating-voltage waveforms are not all sine waves. They may be distorted wave- forms caused by harmonics superimposed on the fundamental wave.
![clip_image002[1]_thumb clip_image002[1]_thumb](http://lh4.ggpht.com/-AzAnqAw85gE/VK1_fVqNcUI/AAAAAAABCTw/TQepvl2pM0s/clip_image002%25255B1%25255D_thumb_thumb.gif?imgmax=800)
![clip_image002[2]_thumb clip_image002[2]_thumb](http://lh4.ggpht.com/-jdWQhJLmQiQ/VK1_h9JPd_I/AAAAAAABCUA/cGw8BEvyoLw/clip_image002%25255B2%25255D_thumb_thumb.gif?imgmax=800) Achievement Review
Achievement Review
1. State four reasons why most electrical energy produced is generated by alternators rather than by direct-current generators.
2. List five applications in which direct current is preferred over alternating current.
3. Name several ways by which alternating current is changed or rectified into direct current.
4. Explain the difference between the rotating line method and the rotating coil method of generating a sine wave.
5. Assuming that the rotating line of Figure 1–8 has a length of one unit, determine its projection or shadow on the X and Y axes at 30°, 45°, 120°, and 240°. (Refer to Figure 1–5 and Appendices 4 and 5.)
6. Prove that tan 8 = (sin 8)/(cos 8). (Refer to Figure 1–5.)
7. Using the answers to question 5, determine the tangents for 30°, 45°, 120°, and 240°. (Refer to Figure 1–5.) Check the answers with Appendices 4 and 5.
8. A sine-wave voltage produced by an ac generator has a maximum value of 170 V. Determine the instantaneous voltage at 45 electrical degrees after crossing the zero axis in a positive direction.
9. Determine the instantaneous voltage of the generator in question 8 at 240 electrical degrees.
10. The speed of a six-pole alternator is 1200 r/min. Determine the frequency of the output of the generator.
11. A 25-Hz alternator has two poles. Determine the speed of the alternator in r/min.
12. Two ac generators are to be operated in parallel at the same frequency. Alternator 1 has four poles and turns at a speed of 1800 r/min. Alternator 2 has 10 poles.
a. What is the frequency of alternator 1?
b. What speed must alternator 2 have so that it can operate in parallel with alternator 1?
13. Explain the difference between electrical time degrees and mechanical degrees.
14. Define (a) cycle, (b) alternation, (c) frequency.
15. Why is 60-Hz alternating-current service preferred to a frequency of 25 Hz in most areas of the United States and Canada?
16. Plot a sine wave of voltage for 360° or one cycle. The voltage has an instantaneous maximum value of 300 V.
17. Explain what is meant by a fundamental sine wave with a triple-frequency harmonic.
18. What is the advantage in using a frequency higher than 60 Hz for the electrical systems of various types of aircraft?
19.

![image_thumb[8] image_thumb[8]](http://lh4.ggpht.com/-qxQA87ek9DQ/VK1-x9hjzHI/AAAAAAABCQA/ILvBbgC5a3c/image_thumb%25255B8%25255D_thumb.png?imgmax=800)
![image_thumb[9] image_thumb[9]](http://lh5.ggpht.com/-UrVVH9VDpj8/VK1-2iZ1-zI/AAAAAAABCQQ/1XOjwYm1czY/image_thumb%25255B9%25255D_thumb.png?imgmax=800)
![image_thumb[10] image_thumb[10]](http://lh4.ggpht.com/-6m1pfzV7JP4/VK1-5RZNRdI/AAAAAAABCQg/3SFAfweVSM4/image_thumb%25255B10%25255D_thumb.png?imgmax=800)
![image_thumb[13] image_thumb[13]](http://lh5.ggpht.com/-MaFjXHtDgqA/VK1_DYp-ZJI/AAAAAAABCRQ/uo1wcas49s8/image_thumb%25255B13%25255D_thumb.png?imgmax=800)
![image_thumb[14] image_thumb[14]](http://lh6.ggpht.com/-S3nlV7l6P9s/VK1_GFQsdZI/AAAAAAABCRg/ZrVO0tcJZuI/image_thumb%25255B14%25255D_thumb.png?imgmax=800)
![image_thumb[15] image_thumb[15]](http://lh3.ggpht.com/-H6mfmkQ_z5A/VK1_JGitHiI/AAAAAAABCRw/pIgMpIeZD0I/image_thumb%25255B15%25255D_thumb.png?imgmax=800)
![image_thumb[16] image_thumb[16]](http://lh5.ggpht.com/-lbN-FMNqLZE/VK1_Lqjd2AI/AAAAAAABCSA/mZwDvraj0Mg/image_thumb%25255B16%25255D_thumb.png?imgmax=800)
![image_thumb[17] image_thumb[17]](http://lh3.ggpht.com/-bLb4k9bYf94/VK1_Omj79qI/AAAAAAABCSQ/0WuE6Slwjuk/image_thumb%25255B17%25255D_thumb.png?imgmax=800)
![image_thumb[18] image_thumb[18]](http://lh5.ggpht.com/-tHCi6FoDeSY/VK1_RN8vvBI/AAAAAAABCSg/tLa2DXgixe4/image_thumb%25255B18%25255D_thumb.png?imgmax=800)
![image_thumb[19] image_thumb[19]](http://lh4.ggpht.com/--CCVIh_wfB0/VK1_UspQNmI/AAAAAAABCSw/mZ6gsEhFY5k/image_thumb%25255B19%25255D_thumb.png?imgmax=800)
![image_thumb[23] image_thumb[23]](http://lh4.ggpht.com/-DjFkrsmXNxQ/VK1_luvor-I/AAAAAAABCUQ/vnlGy_r9AWI/image_thumb%25255B23%25255D_thumb.png?imgmax=800)