The Revolving Magnetic Field of the Stator
When three-phase voltages are applied to the stator-winding terminals, balanced three-phase currents flow in the phase windings and a rotating magnetic field is produced in the air gap of the machine. This field induces an emf in the rotor winding shorted together or connected in series with a starting rheostat. The currents thus induced produce a revolving magnetic field of their own. The speed and direction of rotation of the two fields are the same, so they combine to yield the operating revolving field of the machine.
Consider the revolving stator field, assuming that the rotor circuit is open. Above all this field depends on the geometric arrangement of the-phase windings on the stator.
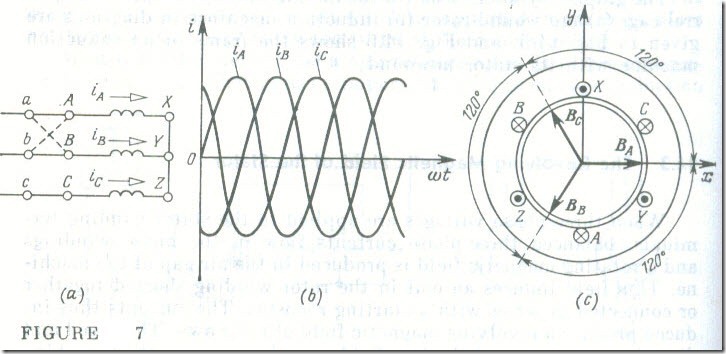
A two-pole revolving field. A two-pole revolving field will be produced when the three identical phase windings are positioned on the stator so that they are spaced 1200 apart. In Fig. 7 c , each phase winding is represented by a single turn and has its terminals labelled as A, B, and C for the starts, and X, Y and Z for the finishes. When the phase windings are connected in a star (see Fig. 7 a) or in a delta and energized from a three-phase power supply, the co-il turns will carry the following currents:
iA = Imsin ɷt
iB = Imsin (ɷt – 120°)
ic = Imsin (ɷt – 240°)
(see Fig. 7 b). The currents in the phase windings produce magnetic fields with the respective magnetic inductions given by
BA = Bmsin ɷt
BB = Bmsin ( ɷt – 120°) (14.1 )
Bc = Bmsin ( ɷt – 240°)
The pattern of the magnetic induction vectors is shown in Fig. 7 c. On combining vectorially , the magnetic inductions yield the magnetic induction due to the resultant stator field.
The properties of the resultant stator field can conveniently be defined in terms of its components directed along two mutually perpendicular axes, and y , with the z-axis assumed to be along the axis of the phase A coil.
Now we set out to determine the magnetic field component along the -ax is. It is equal to the algebraic sum of the projections of the three instantaneous magnetic inductions on that axis
B = BA cos 0° + BBCOS (-120°) + Bc cos (-240°)
= BA + BB ( – 1/2) + Bc ( – 1/2)
On substituting for the magnetic inductions from Eq.(14. 1) , we get
B = Bm [sin ɷt – ½ sin (ɷt – 2π/3) – ½ sin (ɷt – 4π/3) ]
= Bm [sin ɷt – ¼ sin ɷt + √3/4 cos ɷt + ¼ sin ɷt – √3/4 cos ɷt ] = 1.5Bm sin ɷt (14. 2)
The magnetic field component along the y-axis is
By = BA sin 0°+ BB sin (-120°) +Bc sin (-240°)
=BB (-√3/2)+Bc √3/2
Or, on substituting for the magnetic inductions from Eq. (14.1),
By=Bm [ – √3/2 sin (ɷt -2π/3) + √ 3/2 sin (ɷt -4π/3)]
= 1.5Bm cos ɷt ( 14.3)
Thus the resultant magnetic induction of the stator field
Bst = √ (B2 + B2y ) = 1.5Bm √(sin2 ɷt + cos2 ɷt ) = 1.5Bm (14.4)
is constant in magnitude and the angle ex between the magnetic lines of force and the y-axis is such that
tan a = B / By = sin ɷt /cos ɷt = tan ɷt
Hence,
a = ɷt
In other words, the magnetic field of the stator revolves clockwise at a constant speed ɷ in the plane containing the coil axes. It is consecutively aligned with the axis of that phase winding in which the current is a maximum. This means that it revolves in the direction of the phase sequence of the three-phase system of currents in the phase windings.
The direction of rotation of the stator field can be reversed by simply interchanging the connection of any two phase windings to a three-phase power supply, such as shown dashed in Fig. 7 a.
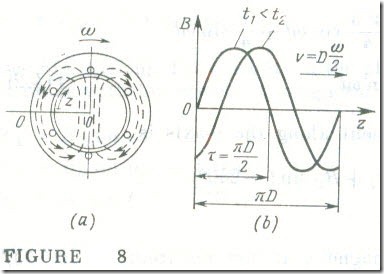
The overall distribution of the magnetic lines of force in the revolving stator field of a two-pole induction machine at time t1 is shown in Fig. 8 a. The distribution of the magnetic induction
B in the air gap between the stator and rotor as a function of the distance z from the line O-O taken as reference at times tl and t2 > tl is shown in Fig. 8 b. The linear speed at which the magnetic field travels along the air gap depends on the diameter D and is equal to ν = Dɷ/2 . At the commercial frequency (f = 50 Hz), the stator magnetic field of a two-pole induction machine revolves at n = 50 X 60 = 3000 rpm. In most practical cases, motors are made to have a lower speed. This is achieved through the use of multipole stator windings.
A multipole revolving field. In the case of a multipole stator winding, each pole pair of the revolving field corresponds to one coil group in each phase winding, which works out to just three coil .groups for three phase windings. Therefore, if the field is to have p pole pairs, the three phase windings must be divided into
k =3p (14.5)
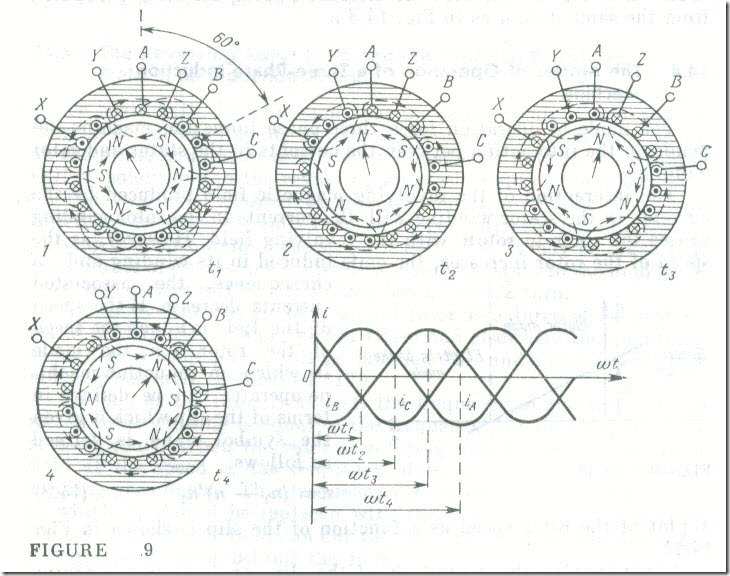
equal parts, or p parts per phase. As an example, Fig. 9 shows a simplified diagram of the stator winding of a six-pole (p = 3) machine. Here the phase windings are divided into 3p = 9 parts, and each phase winding into three parts. In the simplified diagram each coil group of a phase winding is shown as a single-turn coil and the connections are labelled only for phase A , with the connections made on the rear side of the stator core being shown dashed. In a multipole machine, the sides of such a coil group are spaced 180o/p, or one pole pitch τ . apart along the stator periphery. For a six-pole machine this angle is 180°/3 = 60°.
Figure 9 also shows the waveforms of instantaneous stator currents making up a balanced three-phase system. The magnetic field patterns labelled 1 through 4 are given for instants tl through t4 . The directions of currents in the phase conductors shown in the leftmost figure correspond to time tl when the current in the first phase is a maximum. In accord with these current directions, the magnetic lines of force produced by the stator enter the rotor at three points and leave it likewise at three points, thus forming three pole pairs (p = 3). At time t2 , the directions of currents and, as a consequence, the position of the stator field are changed. During one cycle of alternating current the magnetic field moves through one-third of a circle, that is, through the arc occupied by the phase windings on the stator. This arc corresponds to two pole pairs (2p) of the revolving
field and is called the double pole pitch, 2’1′. Thus, the pole pitch ‘1’ is the arc of the stator circumference corresponding to one pole of the magnetic field
τ = πD/2p (14.6)
where D is the inside diameter of the stator core.
During one cycle, T, of alternating current the revolving field of the stator moves through one double pole pitch, 2τ ,
and completes one revolution during p cycles. Thus, every second the field completes 1/pT = f / p revolutions, and the speed (in rpm) is
n1 = f X 60/p (14.7)
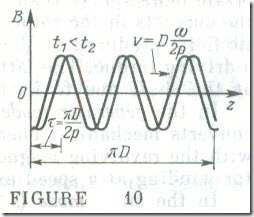
The distribution of magnetic induction B due to the stator magnetic field in the air gap of a six-pole machine at times tl and t2 is shown in Fig. 10, with the distance z along the air gap counted from the same datum as in Fig. 8 a.