Transformers in Parallel

Transformers in Parallel

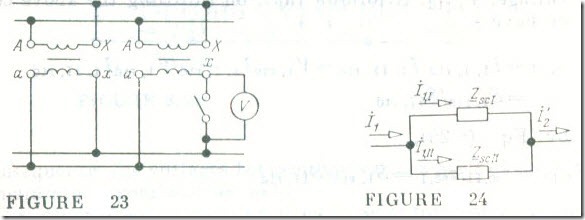
When two (or more) transformers are used in parallel, their pri­mary windings are energized from a common source (a common power line in Fig.23), and their secondary windings are connected across a common load (a common line in Fig 23).

Transformers to be brought in for parallel operation should meet three conditions of which one is mandatory and the remaining two permit some variations. These conditions are as follows.

(1) The transformers should have the same phase displacement , that is belong to the same reference group (for three-phase transfor­mers , this should be either reference group 0 or 11).

(2) The transformers should have the same rated primary and sec­ondary voltages, and the difference in transformation ratio ought not to exceed 0.5 %.

(3) the transformers should have the same impedance voltage (to within ± 10%).

Meeting the first two conditions avoids heavy circulating cur­rents in the transformer windings which would otherwise flow at no-­load if the paralleled transformers belonged 10 displacement phase dis­placement groups or differed ill secondary emfs .

For single-phase units, a further requirement is the correct polar­ity on the secondary side. This requirement is checked as follows. One single-phase transformer is connected in parallel with another as shown in Fig.23, and a voltmeter is placed in parallel with the knife-blade switch which serves to turn On the second transformer . If the secondary connection is correct. the voltmeter will read zero: otherwise the voltmeter will read twice the secondary voltage of the transformer .

In the case of failure to meet the first requirement when connect­ing in parallel two three-phase units, the phase displacement be­tween the secondary line voltages will he 30°. Therefore a resultant emf will be induced in each loop formed by two phase windings (of the two transformers). Since the resistance of the windings is small, this emf will produce a very heavy current detrimental to the transformer windings.

It is important to satisfy the third condition in order that the load will be shared between the parallel transformers in proportion to their apparent power ratings. In the simplified equivalent circuit of Fig. 17 a transformer is represented by a circuit in which the complex short-circuit impedance is Z_sc ( see Sec. 7). Two transformers in parallel may be shown in n common equivalent circuit as two parallel branches containing short-circuit impedance Z_sc,I and  Z_sc,II (Fig. 24). With this arrangement, the rms currents I₁,_I and I₁,_II are inversely proportional to the impedances of the parallel branches

I₁,_I/I_1,II = z_sc,_II /z_sc,_I (8.25)

The impedance voltage of a transformer is proportional to the product of the rated primary current I₁,_rtd by its short-circuit imped­ance Z_SC . If the two paralleled transformers have the same imped­ance voltage, then

z_sc,I I _I,rtd = z_sc,II I_1,II,rtd

Since the transformers in parallel should have the same primary rated voltage, V₁,_rtd it follows that, on fulfilling the above condi­tion, we have

Z_sc,II/ Z_sc,I =I_1,I,rtd/ I₁,_Irtd = V_1,rtdI_{1, I,rtd} /V_l,rtdI₁, _II,rtd

= S _I,rtd/ S_II,rtd

and, by Eq. (8.25),

I₁,_I/ I_1,II = Z_sc,II/Z_sc,I = S_I,rtd/S_II,rtd

That is, the currents are shared between the paralleled transformers in proportion to their apparent power ratings. In other words, the equality of impedance voltages provides for the distribution of load between the paralleled transformers in proportion to their apparent power ratings.