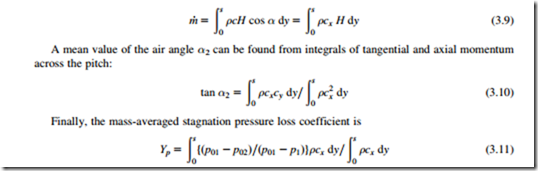Cascade flow characteristics
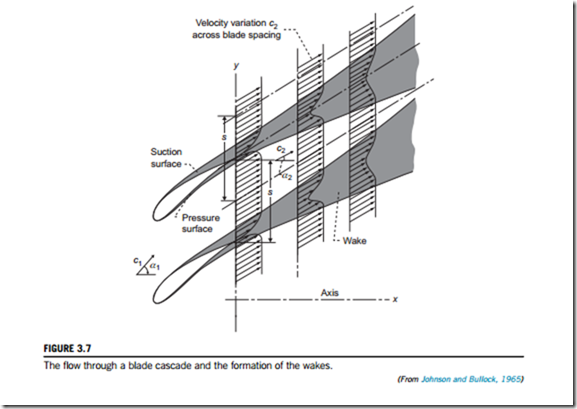
The fluid approaches the cascade from far upstream2 with velocity c1 at an angle α1 and leaves far downstream of the cascade with velocity c2 at an angle α2 as shown in Figure 3.7. The aims of a cascade test are to measure the deviation angle, δ, and to characterize the losses generated within the flow as it is passes through the blade passages.
Deviation arises through inviscid and viscous effects. The flow mechanisms are different for compressors and turbines and they will be described in detail later. Essentially though, the flow is unable to follow the blade angle precisely, such that it is underturned and thus leaves the trailing edge at a slightly different angle to the blade exit angle. Cascade losses arise from the growth of the boundary layers on the suction and pressure surfaces of the blades. These boundary layers combine at the blade trailing edge where they form the blade wake. As a result, a local defect in stagnation pressure is created. As the flow moves downstream the wake widens, as shown in Figure 3.7, and becomes less intense. In addition, cascades operating at high Mach numbers have losses due to shock waves and shock-boundary layer interaction at the blade surfaces.
The deviation and loss for a cascade are measured (or computed) at a range of conditions, because as well as determining the design performance, it is important to check the tolerance to changes in the inlet flow conditions, i.e., to show good off-design behavior. Note that cascade tests can be made on both rotor and stator blades. For rotors, the absolute velocities in the cascade are equivalent to the relative velocities that would be present in the actual machine.
Streamtube thickness variation
When considering the flow through the blade passage of a compressor cascade, it is often assumed that the mean streamtube thickness remains constant. However, this may not be true because the rapid increase in pressure of the flow through the blades can cause a marked thickening of the end wall boundary layers resulting in an effective contraction of the flow as already indicated in Figure 3.3. This effect can be countered by the use of suction to remove the end wall boundary layers.
In general, for all flows, the conservation of mass flow rate per blade passage is
where Hs is the projected frontal area of the control volume, Aa. The parameter H1s cos α1 is the flow area measured perpendicular to the inlet flow direction. This is the area perceived by the flow and is therefore referred to as the true flow area. This is an important factor when compressible flow is considered.
It is useful to define an axial velocity density ratio (AVDR), i.e.,
Equation (3.4) can be used in relating flow properties at the different positions along the mean streamtube. Note that AVDR is the inverse of the contraction coefficient described in the introduction. In compressors AVDR . 1 due to the thickening boundary layers, but in turbine cascades AVDR may be less than 1 due to the possible thinning of the boundary layers in accelerating flow.
Cascade performance parameters
For a known AVDR, as just defined, the primary aerodynamic input data for a cascade test are:
i. the inlet flow angle, α1;
ii. the inlet Mach number, M1;
iii. the blade Reynolds number, Re 5 ρ1c1l=μ, where l is the blade chord.
The data from cascade traverses are used to provide the following parameters for use in the design and performance prediction of axial flow compressors and turbines:
i. exit flow angle, α2;
ii. stagnation pressure loss, Yp, or an energy loss coefficient, ζ.
The performance characteristics of a cascade can therefore be expressed by the following functional relationships:
The exit flow angle, α2, is a critical performance parameter because it determines the work transfer within a turbomachinery stage. If we revisit the Euler work equation from Chapter 1, Δh0 5 Δ(Ucθ), it is clear that the work input or output from a turbomachine will depend on the exit flow angles since cθ 5 c sin α.
The stagnation pressure loss coefficient is an overall measure of the aerodynamic losses through the blade row. Generally, it is defined as Yp 5 loss of stagnation pressure4reference ðdynamicÞ pressure The aerodynamic losses in a cascade blade row translate into efficiency losses within a real turbomachine with the same blade shapes. The sources of losses can include:
i. boundary layers on the blades;
ii. flow separation;
iii. shock waves in the flow.
If no shock waves are present, most of the “loss” due to irreversibility is confined to a narrow wake downstream of the trailing edge as shown in Figure 3.7.
For compressors, the total pressure loss coefficient is based on reference inlet conditions, i.e.,
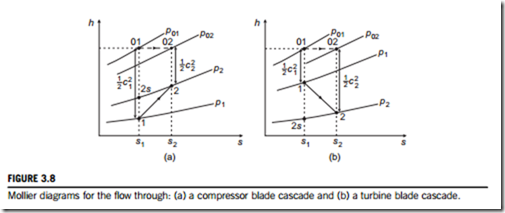
A Mollier diagram with the pressures and salient points for a compressor blade cascade is shown in Figure 3.8(a).
For turbines, the total pressure loss coefficient is based on reference exit conditions, i.e.,
In this case the reference dynamic pressure is the dynamic pressure at exit if the flow were isentropic. Other variations of the turbine loss coefficient are used in the literature and Horlock (1966) gives a comprehensive list of the definitions possible.
An alternative loss parameter is sometimes used for turbines, called the energy loss coefficient, ζ, which measures the lost kinetic energy relative to the isentropic exit kinetic energy:
Figure 3.8(b) is a Mollier diagram3 indicating the pressures and enthalpies for the flow through a turbine cascade blade row.
The two definitions of loss coefficient yield numerical values that are almost identical at low Mach numbers, but their values rapidly diverge as M2 increases with Yp . ζ.
A primary objective of a compressor blade is to produce a rise in static pressure as well as a deflection of the flow angle. A relevant performance parameter is, therefore, the static pressure rise coefficient. For compressible flow this is usually defined as
Flow measurements are made usually across either one or two blade pitches of the varying values of stagnation and static pressures, p02 and p2, and the values of α2. Mass-averaged values of the performance parameters are then derived from these flow measurements. For example, the mass flow rate is given by
Figure 3.9 shows representative traverse results of Yp and α2 for a compressor cascade together with the mass-averaged values of these parameters. The odd-looking “kinks” in the plot of α2 are caused by the variation in the gradient of p02 across the wake and the response of a yaw meter used in measuring flow direction. Further details are given in a paper by Dixon (1978).
Note: From this point onward, all parameters, e.g., α2, Yp, are taken as having been mass-averaged according to the formulae just outlined.
Blade surface velocity distributions
The details of the flow and velocity variations within the blade passages are not required to derive the cascade performance metrics. However, blade surface velocity (and pressure) distributions are used to show whether a blade achieves the velocity distributions intended in the design, and they are helpful for understanding the way a cascade blade performs. In particular, the velocity variation on the blade suction surface can give an indication of imminent flow separation, which would lead to reduced turning and high loss. The relationship between surface velocity distribution and blade performance is discussed further in Section 3.5.