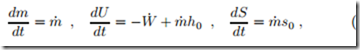Reversible Filling of an Adiabatic Container
When one inflates a bicycle tire with a hand pump, tire and pump become warm. While some of the heat comes from friction in the pump—no seal is friction free—a large part of the heat is due to the rise of temperature of the air being compressed.
To fix ideas we consider the simplest possible case, namely the filling of an adiabatic container with an ideal gas under the assumption that all processes are fully reversible. The system to be considered consists of the adiabatic container of volume V0 and an adiabatic reversible compressor which draws outside air at T0, p0 and compresses it to the pressure p inside the container, which grows over time. Figure 15.6 gives a sketch of the system considered.
When all processes are reversible, it is convenient to set the system bound- ary such that the system contains container and compressor. Then, the balances for mass, energy and entropy become
where W˙ is the power to run the compressor, and m˙ is the mass flow pushed into the container. There is no generation of entropy due to the assumption of reversibility. We assume that initially the container is in equilibrium with the environment, so that it contains the mass m0 = p0 V0 , and that the mass flow has the same value at all times, i.e., m˙ = const. Integration of the mass balance gives the mass in the container at time t as m (t) = m˙ t + m0 . (15.31) The entropy balance can be integrated easily, to give
The air inside the container is compressed adiabatically, as is the intake air when it passes through the compressor.
Since the pressure rises, the power to drive the compressor is increasing over time. From the first law, with U = mu = mcv T , h0 = cpT0, we find