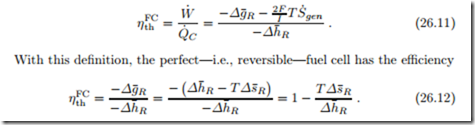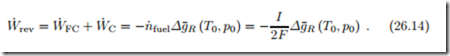Fuel Cell Efficiency
Efficiencies of engines are normally defined as
where for power producing heat engines the gain is the power produced, and the expense is the heat put into the engine through the combustion of fuel, nuclear reactions, etc. Fuel cells are not heat engines, and thus the question arises how to best define their efficiency. The gain is the power produced, hence this is a question of defining the expense.
For comparison of heat engines and fuel cells the following definition is of- ten used: In a combustion process one could obtain the heat Q˙ C = −ΛΔh¯R =− 2F Δh¯R. Considering this heat as the expense, one defines the “thermal efficiency” of a fuel cell as
For all fuels Δh¯R < 0, but there is no definite sign for the entropy of reaction Δs¯R. For the hydrogen reaction, Δs¯R < 0 and thus ηFC < 1 for reversible fuel cells (irreversible fuel cells have even smaller efficiencies, of course). However, there are reactions, in particular the reaction between carbon and oxygen, C + O2 :;: CO2, in direct carbon fuel cells, for which the entropy of reaction is positive, Δs¯R > 0, so that ηFC as given in (26.11) becomes larger than unity. A proper efficiency measure should always assume values between zero and unity. It follows that the efficiency definition (26.11) is not suitable for the evaluation of fuel cells.
In order to understand why this efficiency measure can be above unity, one needs to consider that, according to the second law, the heat exchanged with the surroundings for the reversible fuel cell is T Δs¯R. If T Δs¯R < 0, heat is rejected into the surroundings, but if T Δs¯R > 0, heat is imported from the surroundings.
One should not be surprised that this efficiency definition leads to problems, since the heat of reaction, −Δh¯R, is not relevant in the thermodynamics of fuel cells, as is apparent in that it does not appear in the discussion of fuel cell power and voltage. Heat of reaction is a quantity relevant only for combustion systems.
A more meaningful efficiency is the ratio of the actual power produced by the fuel cell and the maximum power that could be obtained from the fuel, in a fully reversible process. This leads to the second law efficiency,
All three quantities decrease with increasing temperature. Thus, if one con- siders a fuel cell alone, one will gain more work at lower temperatures. High temperature fuel cells, e.g. solid oxide fuel cells, operate at temperatures be- tween 700 and 1000 ◦C, and thus have lower open circuit voltages than low temperature fuel cells. However, due to the high temperatures, the activation losses (see below) are lower, and expensive catalysts are not required. More- over, the heat rejected from high temperature fuel cells can be used to drive heat engines in a combined cycle to produce additional power. If the heat is barely rejected into the environment, there is an external loss.
In other words, fuel cells must be imbedded into a system, where the fuel cell is at the center, but additional systems for extracting work, heating and cooling must be considered as well. In order to clarify this, Fig. 26.4 shows a (reversible) fuel cell operating at temperature T as part of a fully reversible external system, where the incoming fuel and oxidizer are heated to T by a series of infinitesimal Carnot heat pumps, the heat Q˙ FC rejected from the fuel cell drives a Carnot heat engine, and the exhaust is cooled through infinitesimal Carnot heat engines so that it leaves at T0. Of course, other fully reversible set-ups are possible, e.g., some heat could be exchanged be- tween the incoming reactant streams and the product stream, using reversible counter-flow heat exchangers. Heat is only exchanged at environmental temperature, and since all incoming and outgoing mass flows are at T0 and since the system exchanges heat only at T0, and when all flows are at p0, the work produced per mole of fuel is given by (25.18),
Thus, the obvious definition of a second law efficiency for a fuel consuming system is the relative amount of the work that is actually produced from the available work, i.e.,
This definition can be used for the evaluation of any fuel consuming power generation device that is embedded in the environmental at T0. The relation between the second law efficiency and the thermal efficiency is
to account for losses in heat exchanger and exhaust; Q˙ C is the heat actually transmitted into the heat engine, while −Δh¯R is the available heat.
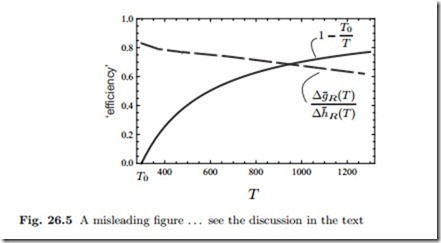
To finish this section we present and criticize a misleading figure that is sometimes found in the fuel cell literature. Figure 26.5 shows the thermal efficiency (26.11) of a reversible hydrogen fuel cell, ηFC = Δg¯R (T ) , and the efficiency of a Carnot heat engine, ηC = 1− T0 , both plotted over temperature T . The Carnot efficiency η grows with temperature, whileΔg¯R ( T ) decreases.
The figure seems to imply that at higher temperatures fuel cell efficiency might not be as good as the efficiency of a heat engine.
This interpretation is misleading for two reasons: (a) As discussed above, a high temperature fuel cell must be seen as one element in a larger system that includes heat engines to convert the high temperature heat rejected from the fuel cell and its exhaust. (b) The Carnot efficiency is relevant only for heat engines operating between two reservoirs at constant temperatures T, T0. A heat engine that is driven by the reaction of a fuel does not belong into that category, and thus the Carnot efficiency is not necessarily relevant for a fuel driven engine process.
The proper efficiency measure to compare fuel cell systems and heat engines is the second law efficiency ηII , Eq. (26.15), which relates the actual work produced to the maximum amount that could be produced in a fully reversible process. For real engines, this efficiency is below unity, due to entropy generation in irreversible processes. As discussed in Sec. 25.12, combustion engines suffer from losses in combustion, heat transfer, friction and mixing.
Fuel cells suffer from a different array of irreversible losses that will be discussed below. Whether or not a fuel cell system will have a higher efficiency than a combustion system depends on the details of the design, materials used, and the processes within the system.