Equilibrium in Heterogeneous Systems
The thermodynamic equilibrium conditions, e.g., system entropy assumes a maximum in isolated systems (17.23), or Gibbs free energy assumes a mini- mum when pressure and temperature are prescribed at the boundary (17.30), are universally valid. In this section, we evaluate the equilibrium state for a heterogeneous system, which consists of two parts in thermal and mechanical
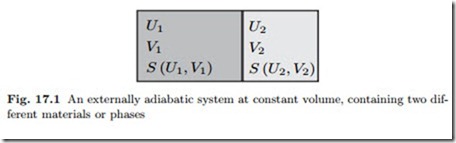
contact. To be specific, we consider an adiabatically enclosed system at constant volume that is divided into two parts as depicted in Fig. 17.1. The two parts may contain different substances, or the same substance, and they might contain different phases. The divider between the two parts can move freely, and is diathermal, i.e., heat can pass, potential and kinetic energies are ignored. Due to the boundary conditions for the system, total energy, U = U1 + U2, and total volume, V = V1 + V2 are constants, but energy and volume of the parts might change. We assume the system is in thermal equilibrium and consider small perturbations from the equilibrium state such that the energies and volumes of the two parts are
This perturbation yields a change in entropy, so that the entropy of the perturbed state is S + δS. Since the perturbed state is an equilibrium state, the entropy S = S1 (U1, V1) + S2 (U2, V2) is a maximum; accordingly, the perturbation in entropy must be negative, δS < 0. We have
Since δU and δV can have arbitrary positive or negative values, the sign condition on δS can only be fulfilled when both terms vanish. This gives the expected equilibrium conditions for the two parts, namely that they have the same temperatures and pressures
The above discussion can be performed for any splitting of the system, and for different substances in the subsystem. It follows that all possible subsystems have the same temperature and pressure, that is pressure and temperature are homogeneous within the system.
If potential energy, e.g., gravitation, plays a role, pressure is not homogeneous, see Sec. 17.3. Pressure distribution within one substance or phase is then given by g (p, T ) = −T Λρ − γz, while the pressure is continuous at the interface between two substances or phases.