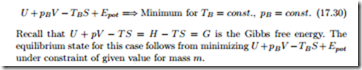Adiabatic and Isobaric System
A Legendre transform gives an alternative form of the first law,
and we conclude that
Note that H = U + pV is the enthalpy. The equilibrium state for this case follows from maximizing entropy under constraints of given values for mass m and U + pB V + Epot.
Isentropic and Isochoric System
For the discussion of non-adiabatic systems, we eliminate the heat Q˙ between the first and the second law, to find
It follows that in a process with constant entropy and constant volume, where the total energy will assume a minimum in equilibrium,
The equilibrium state for this case follows from minimizing energy U + Epot under constraints of given values for mass m and entropy S. Note that entropy is difficult to control, and thus this case is typically not encountered in applications.
Isothermal and Isochoric System
By means of a Legendre transform, (17.26) can be rewritten as
It follows that in a process with constant boundary temperature and volume, where dTB dV = 0, the combination E − TB S assumes a minimum in equilibrium,
Recall that U − TS = F is the Helmholtz free energy. The equilibrium state for this case follows from minimizing U − TB S + Epot under constraint of given value for mass m.
Isothermal and Isobaric System
Another Legendre transform shows that for a process with constant boundary pressure and temperature ( dTB = dpB = 0) the combination E + pB V − TB S assumes a minimum,