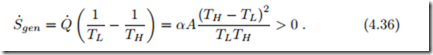Newton’s Law of Cooling
We return to the discussion of heat transfer. The inequality (4.27) requires that Q˙ has the same sign as ![]() a requirement that is fulfilled for a heat transfer rate
a requirement that is fulfilled for a heat transfer rate
Q˙ = αA (TH − TL) (4.35)
with a positive heat transfer coefficient α > 0, and the heat exchange surface area A. This relation, which we already used in an example, is known as New- ton’s law of cooling, and is often used in heat transfer problems. The values of the positive coefficient α must be found from the detailed configuration and conditions in the heat transfer system. The surface area A appears due to the intuitive expectation that enlarging the transfer area leads to a proportional increase in the amount of heat transferred.
Heat transfer was introduced as energy transfer due to temperature difference with heat going from hot to cold, Newton laws of cooling states that as a result of the temperature difference one will observe a response, namely the heat flux.
The procedure to derive Newton’s law of cooling can be described as follows: The entropy generation rate (4.27) is interpreted as the product of a thermodynamic force—here, the temperature difference (TH − TL)—and a corresponding flux—here, the heat flux Q˙ . To ensure positivity of the entropy generation rate, the flux must be proportional to the force, with a positive factor αA that must be measured. The same strategy can be used for other force-flux pairs.
With Newton’s law of cooling it is easy to see that heat transfer over finite temperature differences is an irreversible process. Indeed, the second law (4.27) gives with (4.35)
Only when the temperature difference is infinitesimal, i.e., TH = TL + dT , entropy generation can be ignored, and heat transfer can be considered as a reversible process. This can be seen as follows: For infinitesimal dT the entropy generation rate becomes S˙gen = αA ( dT . Since quadratic terms in infinitesimal differences can be ignored, this implies S˙gen = 0 (dT → 0). In this case, to have a finite amount of heat transferred, the heat exchange area A must go to infinity.
Zeroth Law and Second Law
While above we considered heat transfer between reservoirs, the conclusion is valid for heat conduction between arbitrary systems: As long as the systems are in thermal contact through heat conductors, and their temperatures are different, there will be heat transfer between the systems. Only when the temperatures of the systems are equal, heat transfer will cease. This is the case of thermal equilibrium, where no change in time occurs anymore. This includes that the temperature of an isolated body in thermal equilibrium will be homogeneous, where equilibration occurs through heat transfer within the system.
The zeroth law states: In equilibrium systems in thermal contact assume the same temperature. Thus, the zeroth law of thermodynamics might appear as a special case of the second law. It stands in its own right, however, since it defines temperature as a measurable quantity.