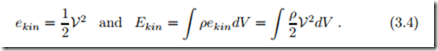Conservation of Energy
It is our daily experience that heat can be converted to work, and that work can be converted to heat. A propeller mounted over a burning candle will spin when the heated air rises due to buoyancy: heat is converted to work. Rubbing your hands makes them warmer: work is converted to heat. Humankind has a long and rich history of making use of both conversions. Friction between a fast spun stick and a resting piece of wood is used since millennia to create a fire. Technical applications of heat to work conversions are abundant through history, and our modern life is unthinkable without heat engines such as steam and gas turbines for generation of electricity, or car and aircraft engines for transport. In cooling engines work is used to withdraw heat, such as in refrigerators or in air conditioning devices.
The evaporation of water to steam by heating provides a large change in volume and/or pressure. Devices using this effect were known already more than 2000 years ago, but they became prevalent with the development of the steam engine. Thermodynamics was initially developed to better understand the processes in steam engines and other conversion devices, so that the understanding can be used to improve the engines.
While the heat-to-work and work-to-heat conversions are readily observable in simple and more complex processes, the governing law is not at all obvious from simple observation. It required groundbreaking thinking and careful experiments to unveil the law of conservation of energy. Due to its importance in thermodynamics, it is also known as the First Law of Thermodynamics.
Expressed in words, the First Law of Thermodynamics reads:
Energy cannot be produced nor destroyed, it can only be transferred, or converted from one form to another. In short, energy is conserved.
It took quite some time to formulate the first law in this simple form, the credit for finding and formulating it goes to Robert Meyer (1814-1878), James Prescott Joule (1818-1889), and Hermann Helmholtz (1821-1894). Through careful measurements and analysis, they recognized that thermal energy, mechanical energy, and electrical energy can be transformed into each other, which implies that energy can be transferred by doing work, as in mechanics, and by heat transfer.
The first law is generally valid, no violation was ever observed. As knowl- edge of physics has developed, other forms of energy had to be included, such as radiative energy, nuclear energy, or the mass-energy equivalence of the theory of relativity, but there is no doubt today that energy is conserved under all circumstances.
We formulate the first law for the simple closed system, depicted again in Fig. 3.1, where all three possibilities to manipulate the system from the outside are indicated. For this system, the conservation law for energy reads
where E is the total energy of the system, Q˙ is the heat transfer rate in or out of the system, and W˙ = W˙ piston + W˙ propeller is the total power—the work per unit time—exchanged with the surroundings.
This equation states that the change of the system’s energy in time (dE/dt) is equal to the energy transferred by heat and work per unit time (Q˙ − W˙ ). The sign convention used is such that heat transferred into the system is positive, and work done by the system is positive.
The SI unit of energy, work, and heat is the Joule, 1 J = 1 N m = 1 kg m ; the SI unit of power and heat transfer rate is the Watt, 1 W = 1 J .
All contributions to the first law (3.1), i.e., energy, work and heat, will be discussed in detail in the following sections.
Total Energy
The total energy E of the system is the sum of its kinetic energy Ekin , potential energy Epot, and internal—or thermal—energy U ,
Presently, these are the only forms of energy that we need for the description of thermal processes; other forms of energy that can be relevant are chemical energy, nuclear energy, radiative energy and electrical energy, which will be introduced when required.
We address the different contributions to energy in the next sections.
Kinetic Energy
The kinetic energy is well-known from mechanics. For a homogeneous system of mass m and velocity V, kinetic energy is given by
For inhomogeneous states the total kinetic energy of the system is obtained by integration of the specific kinetic energy ekin over all mass elements dm = ρdV ; we have
Potential Energy
Also the potential energy in the gravitational field is well-known from mechanics. For a homogeneous system of mass m , potential energy is given by
where z is the elevation of the system’s center of mass over a reference height, and g = 9.81 m is the gravitational acceleration on Earth.
For inhomogeneous states the total potential energy of the system is obtained by integration of the specific potential energy epot over all mass elements dm = ρdV ; we have