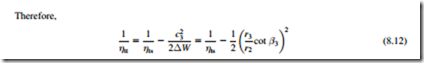Nominal design point efficiency
Referring to Figure 8.4, the total-to-static efficiency in the absence of a diffuser is defined as
EXAMPLE 8.2
Performance data from the CAV type 01 radial turbine (Benson, Cartwright, & Das 1968) operating at a pressure ratio p01/p3 of 1.5 with zero incidence relative flow onto the rotor is presented in the following form:
The turbine is “cold tested” with air heated to 400 K (to prevent condensation erosion of the blades). At nozzle outlet an estimate of the flow angle is given as 70o and the corresponding enthalpy loss coefficient is stated to be 0.065. Assuming that the absolute flow at rotor exit is without swirl and uniform and the relative flow leaves the rotor without any deviation, determine the total-to-static and overall efficiencies of the turbine, the rotor enthalpy loss coefficient, and the rotor relative velocity ratio.
Solution
The data given are obtained from an actual turbine test and, even though the bearing friction loss has been corrected, there is an additional reduction in the specific work delivered due to disk friction and tip leakage losses, etc. The rotor speed Ω 5 the rotor tip speed U2 5 πΩD2/60 5 183 m/s and, hence, the specific work done by the rotor ΔW 5 U2 5 33:48 kJ=kg. The corresponding isentropic total-to-static enthalpy drop is
It is worth commenting that higher total-to-static efficiencies have been obtained in other small radial turbines operating at higher pressure ratios. Rodgers (1969) has suggested that total-to-static efficiencies in excess of 90% for pressure ratios up to 5-1 can be attained. Nusbaum and Kofskey (1969) reported an experimental value of 88.8% for a small radial turbine (fitted with an outlet diffuser, admittedly!) at a pressure ratio p01/p4 of 1.763. In the design point exercise just given the high rotor enthalpy loss coefficient and the corresponding relatively low total-to-static efficiency may well be related to the low relative velocity ratio determined on the hub. Matters are probably worse than this as the calculation is based only on a simple one- dimensional treatment. In determining velocity ratios across the rotor, account should also be taken of the effect of blade-to-blade velocity variation (outlined in this chapter) as well as viscous effects. The number of vanes in the rotor (10) may be insufficient on the basis of Jamieson’s theory (1955), included later in this chapter, which suggests 18 vanes (i.e., Zmin 5 2π tan α2). For this turbine, at lower nozzle exit angles, Eq. (8.13) suggests that the relative velocity ratio becomes even less favorable despite the fact that the Jamieson blade spacing criterion is being approached. (For Z 5 10, the optimum value of α2 is about 58o.)
Some Mach number relations
Assuming the fluid is a perfect gas, expressions can be deduced for the important Mach numbers in the turbine. At nozzle outlet, the absolute Mach number at the nominal design point is