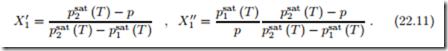Phase Diagrams for Binary Mixtures
For the case of binary mixtures in liquid-vapor equilibrium, we have ν = 2 and Raoult’s law gives the equations
The variables are (T, p, X/ ,X //), and according to Gibbs’ phase rule there are two degrees of freedom, F = 2, so that when two variables are prescribed, the others are fixed.
In particular, when pressure and temperature are prescribed, the values for the mole fractions in both phases are computed as
For given temperature T , we can draw the two curves into a p-X-diagram. Solving for pressure gives the saturated liquid line,
Figure 22.2 shows a p-X-diagram for fixed T with the two curves that meet for X / = X // = 0 and X / = X // = 1 at the respective saturation pressures.
For the assumptions used, the saturated liquid curve is a straight line.
Also indicated in the figure are three pressures. At p1 the pressure is higher than both saturation pressures, and the there is only one single liquid phase.
At p3 the pressure is lower than both saturation pressures, and there is only one single vapor phase. At the intermediate pressure p2, which lies between the two saturation pressures, the mixture can be found either as pure liquid or pure vapor phase, or it can split into two phases. What happens depends on the overall mole fraction of the mixture X1 = n1 +n1 1 (p2,T ), there is only a single liquid phase, and for X1 ≥ X1 (p2,T ), there is only a single vapor phase. If the mixture splits into two phases, the liquid phase with mole fraction X/ (p2,T ) and the vapor phase with mole fraction X// (p2,T ). The component with the larger vapor pressure (here component 1) is more volatile, i.e. more keen to evaporate, and the vapor is richer in the more volatile component while the liquid is depleted of it.
The equations (22.12, 22.13) can be numerically solved for T ; this requires equations or tables for the saturation pressures psat (T ). The resulting T-X- diagram for constant pressure is sketched in Fig. 22.3. The interpretation of the diagram follows the same lines as for the p-X-diagram: For temperatures above both saturation temperatures T sat (p), e.g., T7, the mixture will be pure vapor for all values X1. The mixture will be pure liquid for temperatures below both saturation temperatures, e.g., T0 in the figure. For temperatures between the two saturation temperatures (T1 to T6), the mixture will split into two phases at X/ (T, p) and X // (T, p), if the overall mole fraction X1 lies between these values; else the mixture is either liquid (for X1 ≤ X / (T, p)) or vapor (for X1 ≥ X // (T, p)).
Distillation
Distillation is a separation procedure based on the different compositions of vapor and liquid mixture in equilibrium. Figure 22.4 shows a sketch for a bubble tray column for distillation that matches the T-X-diagram of Fig. 22.3. A temperature gradient is imposed by heating at the bottom and cooling at the top of the column. Several bubble trays are inserted in the column. Industrial columns have up to 100 trays and can reach heights of 60 metres. Heating at the bottom generates vapor that rises in the column, while liquid is generated by condensation at the cooled top and drips down.
On the trays, which all have different temperatures following the temperature gradient established in the column, the rising vapor passes as bubbles through the liquid. This contact between vapor and liquid establishes thermodynamic equilibrium on the tray, determined by the pressure in the column and the temperature on the tray. Consider the tray at T3: The vapor leaving the tray upwards has the mole fraction X// (T3) while the liquid dripping down has the mole fraction X/ (T3). Figure 22.5 illustrates how liquid and vapor pass through the tray: The vapor is forced to bubble through the liquid, and this leads to exchange of components and energy.
For the mixture shown in Figs. 22.3 and 22.4, component 1 is more volatile, so that the vapor becomes richer in component 1 as it ascends, while the liquid becomes richer in component 2 as it descends.
The design and dimensioning of distillation columns is the task of chemical engineers and will not be discussed further. Obviously, distillation becomes more complex when multicomponent mixtures are involved, when saturation temperatures of components are close, and when the mixtures exhibit nonideal behavior, e.g., azeotropes, see Sec. 22.11.