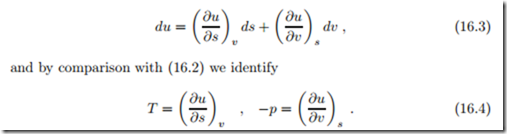Thermodynamic Potentials and Maxwell Relations
We rewrite the Gibbs equation as
This equation suggests to consider the internal energy u as a function of entropy s and volume v, that is u (s, v). Its exact differential (u is a state function) is given by
Thus, the internal energy u (s, v) is a potential, in the sense that temperature T (s, v) and pressure p (s, v) are obtained from derivatives of u.
The order of second derivatives can be exchanged,
For the novice, expressions like (16.6) seem to be just mathematical symbols. However, all expressions have a clear meaning which derives from the properties they entail. For instance, the expression ( ∂T ) gives the change of temperature with volume at constant entropy. It can be measured, in principle, by varying the volume of the system by a small amount dv while the entropy s stays constant, and measuring the associated change in temperature dT . Similarly, the expression ( ∂p describes the change of pressure with entropy at constant volume. It can be measured, in principle, in a system at constant volume v by varying the entropy by ds and recording the associated pressure change dp. Similar interpretations apply to the expressions in (16.4).
The above partial derivatives are, in fact, not accessible to measurements since one of the variables is entropy: since there is no direct measurement of entropy, it is very difficult, if not impossible, to conduct an experiment in which entropy is changed by a given amount ds, or fixed at a given value s.1 To find more relations of the same kind, we use that −pdv = −d (pv)+vdp, which leads to a shift in variables from v to p, a so-called Legendre transform (Adrien-Marie Legendre, 1752-1833). With this, the Gibbs equation (16.2) becomes du = T ds + vdp − d (pv), and by introducing enthalpy as
The last equation is the Maxwell equation for this potential, it results from exchanging the order of derivatives, ∂ h = ∂ h . Again all partial derivatives contain the entropy s as one of the variables, and therefore they are not accessible to measurements.
Similarly, we can apply a Legendre transform to the term T ds = d (T s) −sdT in the Gibbs equation. This transformation exchanges the variable s, which cannot be measured directly, by the variable T , which can be measured.
As a result, we find new potentials, the free energies.
The Helmholtz free energy is defined as
The last equation is the Maxwell equation for this potential, it results from exchanging the order of derivatives, ∂ f 2 ∂T ∂v Maxwell relation (16.11)3 contains the expression ( ∂p , which describes ∂T v the change of pressure p with temperature T in an experiment at constant volume v. Since p, T and v can be measured, this expression can be found experimentally. In fact, measurement of {p, T , v} gives the thermal equation of state p (T, v), and we can say that ( ∂p can be determined from the thermal equation of state. The other expression, ( ∂s ), cannot be ∂v T measured by itself, since it contains entropy s. Hence, with the Maxwell relation the expression ( ∂s ) can be measured through measurement of the ∂v T thermal equation of state.
The Gibbs free energy is defined as
The last equation is the Maxwell equation for this potential, it results from exchanging the order of derivatives, ∂ g = ∂ g . Also this Maxwell relation contains one expression that can be determined from the thermal equation of state, namely ( ∂v ) , relating it to an expression that is not accessible to direct measurement, namely ( ∂s . The usefulness of the above differential ∂p T relations, in particular of those that involve expressions that can be measured, will become evident in the subsequent sections.
It is important to note that the thermodynamic properties u, h, f, g are only potentials when considered as functions of the given variables. That is only u (s, v), h (s, p), f (T, v), g (T, p) are potentials! One can use property relations to change the variables, for instance with the thermal equation of state p (T, v) one obtains g (T, p) = g (T, p (T, v)) = g (T, v)—however, as function of T and v the Gibbs free energy is not a potential.