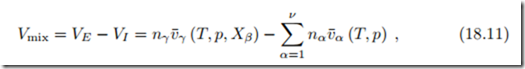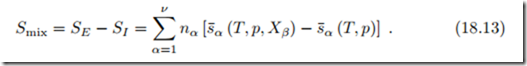Mixing Volume, Heat of Mixing and Entropy of Mixing
As components are mixed at constant temperature and pressure the extensive properties might change. To properly account for the change, we consider ν components in an initial unmixed state (I) where each component is at the same temperature, T , and pressure, p. The components are mixed while keeping temperature and pressure constant, the final state (E) is a homogeneous mixture, see Fig. 18.1. We ask for the corresponding changes in total volume, total enthalpy, and total entropy.
The volume change between initial and final state is computed as1
where v¯α (T, p) denotes the specific volume of component α alone at (T, p) and v¯γ (T, p, Xβ ) denotes the specific volume of any component γ in the mixture of composition Xβ (β = 1,... , ν) at (T, p). Note that in the mixed state all components are distributed over the volume of the mixture, VE .
The change of volume is due to spatial hindrances or advantages on the molecular scale. For instance a mixture of 1 litre of water with 1 litre of ethanol (C2H5OH) yields a mixing volume of 1.93 litres.
When volume ratios are used to define the composition of a mixture, it must be clarified whether the volume of the component is related to the volume of the mixture, VE , or the to the total volume of the components before mixing, VI . A widely used measure for the alcohol content of beverages is “percent of alcohol by volume”, defined as volume of the ethanol component alone over total volume of the mixture,
Isothermal mixing of components might release or require heat, which must be transferred. The first law applied to the isothermal and isobaric mixing process yields
where Hmix is the heat that must be exchanged in order to keep the tempera- ture T constant for the mixing process. Here, ¯hα (T, p) is the molar enthalpy of component α alone at (T, p) and h¯α (T, p, Xβ ) is the molar enthalpy of the component α in a mixture of composition Xβ (β = 1,... , ν) at (T, p).
The enthalpy and internal energy are influenced by the interaction poten- tial between molecules. In a pure substance, particles of type α interact only with particles of the same type. In a mixture, however, particles of type α are surrounded by different types of particles β (β = 1,…, ν), which leads to different molecular interaction potentials, and thus a change in internal energy u¯α and enthalpy h¯α for the particles of type α as compared to the pure substance. A more detailed exploration of this will come in Sec. 22.9.
The entropy of mixing is computed in the same way, as
We shall discuss the enthalpy and entropy of mixing as we proceed. To simplify the discussion we shall ignore volume changes from now on.