Osmotic Power Plant with Irreversibilities
Saltwater at 25 ◦C, 1 bar is pumped to a pressure of 22 bar, and then flows along a semi- permeable membrane, through which fresh water enters and dilutes the saltwater. Due to pressure loss in the desalination system, the exiting solution (diluted saltwater) leaves the desalinator at a pressure of 19 bar. This flow drives a turbine, and leaves the system at 1 bar. Assume that the temperature remains constant throughout the device, and that pump and turbine are irreversible with isentropic efficiencies of 0.85.
The incoming saltwater contains 42 g of sodium chloride The mass densities of saltwater and freshwater are given as: ρsw = 1033 kg , ρfw = 1000 kg , and there is no mixing volume.
1. Determine the osmotic pressure of the incoming saltwater.
2. Determine the mole fraction of water in the exiting diluted water.
3. The volume flow of saltwater is 1000 litres/minute. Determine the volume flows of the freshwater drawn in, and of the diluted saltwater that enters the turbine
4. Determine the power required to drive the pump, and the power produced by the turbine. Compute the net work produced per litre of freshwater drawn in.
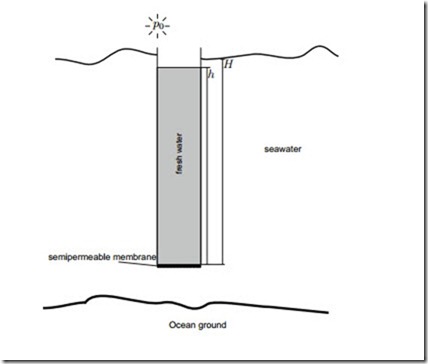
Desalination I
A pipe is closed at one end with a semipermeable membrane which only allows water to pass. The pipe is pressed vertically into an ocean, see the following sketch. The temperature of the ocean is 4 ◦C, and the salt water contains 35 g sodium chloride (NaCl) per litre, moreover
1. To what height H1 must the pipe be immersed, before fresh water passes the membrane?
2. At what height H2 have both, sea water and fresh water, the same height, h = H ? Explain why this is possible.
3. When h > H2 one can run a water wheel with the fresh water leaving the pipe. Of course, this setup is not a perpetual motion engine. Why? (for some discussion see: Scientific American, June 1971, p. 124-125, and April 1972, p110-111). The above calculation assumed constant density of the seawater, and a homogeneous salt content. Can that be expected?
Desalination II
The solution of the previous problem assumed constant density of the seawater. Consider the same problem for the case that the salt concentration follows the barometric law, so that
where Rs is the gas constant for the salt (factor 2 accounts for dissociation) and ρs,0 is a constant specified by the density at the surface (at z = 0). Note that z points upwards, so that the density is larger at greater depth.
1. Discuss the salt concentration profile in the oceans. Under what circumstances would you expect the exponential and the constant profile, respectively?
2. Compute the difference h − H for the exponential profile.
3. Discuss your findings.
Remark: Not all information on the web that you might find on this issue is correct (the same is true for any other topic, of course).
Desalination III
Assume that the salt concentration in a salt water lake follows the barometric (salt density increasing with depth).
A pipe is closed at one end with a semipermeable membrane which only allows water to pass. The pipe is pressed vertically into the lake. The temperature of the lake is 4◦C, and the salt water at the surface contains 20 g sodium chloride (NaCl) per litre. For the following, assume that the density of salt water is given by ρsw = ρfw + ρs where ρw = 1000 kg .
1. To what height H1 must the pipe be immersed, before fresh water passes the membrane?
2. Compute the freshwater height h as a function of sea water height H.
3. Is it possible, that both, sea water and fresh water have the same height, h = H?
Separation
Consider a mixture of three ideal gases, say oxygen, nitrogen and carbon dioxide. Compute the minimum work required to
1. Separate the carbon dioxide from the two other gases
2. Separate all three components.
Partial Separation of a Binary Gas Mixture II
Some carbon dioxide is to be separated from a mixture of nitrogen and carbon dioxide with mole fraction XCO2 = 0.0205. For this, the mixture is pressurized to a pressure of 50 bar, and then flows past a membrane, which allows only CO2 to pass. The CO2 pressure on the back of the membrane is 1 bar.
Determine:
1. The mole fraction of CO2 in the exiting mixture, in the best case.
2. The percentage of CO2 separated from the mixture.
3. The change of the entropy of mixing.
4. The minimum separation work per mole of CO2, when the environment temperature is T0 = 300 K.
Removal of Carbon Dioxide from the Atmosphere
From http://www.virginearth.com/ (2007): The Virgin Earth Challenge is a prize of $25m for whoever can demonstrate to the judges’ satisfaction a commercially viable design which results in the removal of anthropogenic, atmospheric greenhouse gases so as to contribute materially to the stability of Earth’s climate. From Wikipedia: The prize will be awarded to the first scheme that is capable of removing one billion metric tons of carbon dioxide from the atmosphere per year for 10 years.
Let’s evaluate the goal thermodynamically, by computing how much work is necessary.
1. The Earth radius is 6370 km, the pressure at ground level is 1.01325 bar and the gravitational acceleration is 9.81 m . Estimate mass and mole number of Earth’s atmosphere.
2. In January 2014, the mole fraction of CO2 in the atmosphere was 397.80 ppm, up from 393.14 ppm in January 2012 (data from http:// co2now.org/). The pre-industrial level was 284 ppm. Determine mole number and mass of CO2 in the atmosphere, the amount added in the past year, and the amount added since industrialization began.
3. The yearly emissions from fossil fuels and cement production are 33.5 Gt of CO2. Compare this number to the amount added to the atmosphere computed above. Where is the remaining CO2 going?
4. Assume that there is a winner of the competition, the device is built, and 1 billion tons of CO2 are removed in one year. Determine the new mole fraction of CO2 after the year.
5. Compute the minimum work required to remove 10 billion tons from the atmosphere per year (assume T = 290 K and January 2014 composition), and compare to the world energy consumption of about 16 TW, and the world generation of electric power of about 2.5 TW. Also compute the minimum work required to remove the amount added to the atmosphere per year. To simplify, consider a binary mixture of ‘air molecules’ and CO2 molecules.
6. Discuss all results and also the question of irreversibilities in the processes.