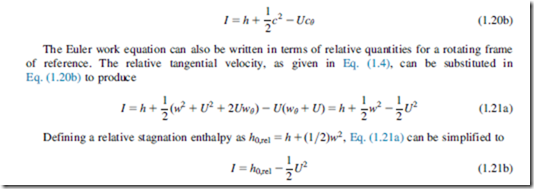The momentum equation
One of the most fundamental and valuable principles in mechanics is Newton’s second law of motion. The momentum equation relates the sum of the external forces acting on a fluid element to its acceleration, or to the rate of change of momentum in the direction of the resultant external force. In the study of turbomachines many applications of the momentum equation can be found, e.g., the force exerted upon a blade in a compressor or turbine cascade caused by the deflection or acceleration of fluid passing the blades.
Considering a system of mass m, the sum of all the body and surface forces acting on m along some arbitrary direction x is equal to the time rate of change of the total x-momentum of the system, i.e.,
Moment of momentum
In dynamics useful information can be obtained by employing Newton’s second law in the form where it applies to the moments of forces. This form is of central importance in the analysis of the energy transfer process in turbomachines.
For a system of mass m, the vector sum of the moments of all external forces acting on the sys- tem about some arbitrary axis A-A fixed in space is equal to the time rate of change of angular momentum of the system about that axis, i.e.,
where r is distance of the mass center from the axis of rotation measured along the normal to the axis and cθ the velocity component mutually perpendicular to both the axis and radius vector r.
For a control volume the law of moment of momentum can be obtained. Figure 1.6 shows the control volume enclosing the rotor of a generalized turbomachine. Swirling fluid enters the control volume at radius r1 with tangential velocity cθ1 and leaves at radius r2 with tangential velocity cθ2. For one-dimensional steady flow,
which states that the sum of the moments of the external forces acting on fluid temporarily occupying the control volume is equal to the net time rate of efflux of angular momentum from the control volume.
Equations (1.19a) and (1.19b) are the general forms of the Euler work equation. By considering the assumptions used in its derivation, this equation can be seen to be valid for adiabatic flow for any streamline through the blade rows of a turbomachine. It is applicable to both viscous and inviscid flow, since the torque provided by the fluid on the blades can be exerted by pressure forces or frictional forces. It is strictly valid only for steady flow but it can also be applied to time-averaged unsteady flow provided the averaging is done over a long enough time period. In all cases, all of the torque from the fluid must be transferred to the blades. Friction on the hub and casing of a turbomachine can cause local changes in angular momentum that are not accounted for in the Euler work equation.
Note that for any stationary blade row, U 5 0 and therefore h0 5 constant. This is to be expected since a stationary blade cannot transfer any work to or from the fluid.
Rothalpy and relative velocities
The Euler work equation, Eq. (1.19), can be rewritten as
where I is a constant along the streamlines through a turbomachine. The function I was first introduced by Wu (1952) and has acquired the widely used name rothalpy, a contraction of rotational stagnation enthalpy, and is a fluid mechanical property of some importance in the study of flow within rotating systems. The rothalpy can also be written in terms of the static enthalpy as
This final form of the Euler work equation shows that, for rotating blade rows, the relative stag- nation enthalpy is constant through the blades provided the blade speed is constant. In other words, h0,rel 5 constant, if the radius of a streamline passing through the blades stays the same. This result is important for analyzing turbomachinery flows in the relative frame of reference.
The second law of thermodynamics—entropy
The second law of thermodynamics, developed rigorously in many modern thermodynamic text- books, e.g., C¸ engel and Boles (1994), Reynolds and Perkins (1977), and Rogers and Mayhew (1992), enables the concept of entropy to be introduced and ideal thermodynamic processes to be defined.
An important and useful corollary of the second law of thermodynamics, known as the Inequality of Clausius, states that, for a system passing through a cycle involving heat exchanges,
where dQ is an element of heat transferred to the system at an absolute temperature T. If all the processes in the cycle are reversible, then dQ 5 dQR, and the equality in Eq. (1.22a) holds true, i.e.,
Thus, for a flow undergoing a process that is both adiabatic and reversible, the entropy will remain unchanged (this type of process is referred to as isentropic). Since turbomachinery is usu- ally adiabatic, or close to adiabatic, an isentropic compression or expansion represents the best pos- sible process that can be achieved. To maximize the efficiency of a turbomachine, the irreversible entropy production ΔSirrev must be minimized, and this is a primary objective of any design.
Several important expressions can be obtained using the preceding definition of entropy. For a system of mass m undergoing a reversible process dQ 5 dQR 5 mTds and dW 5 dWR 5 mpdv. In the absence of motion, gravity, and other effects the first law of thermodynamics, Eq. (1.10b) becomes
Equations (1.26a) and (1.26b) are extremely useful forms of the second law of thermodynamics because the equations are written only in terms of properties of the system (there are no terms involving Q or W). These equations can therefore be applied to a system undergoing any process.
Entropy is a particularly useful property for the analysis of turbomachinery problems. Any increase of entropy in the flow path of a machine can be equated to a certain amount of “lost work” and thus a loss in efficiency. The value of entropy is the same in both the absolute and rela- tive frames of reference (see Figure 1.9) and this means it can be used to track the sources of inefficiency through all the rotating and stationary parts of a machine. The application of entropy to account for lost performance is very powerful and will be demonstrated in later chapters.
Bernoulli’s equation
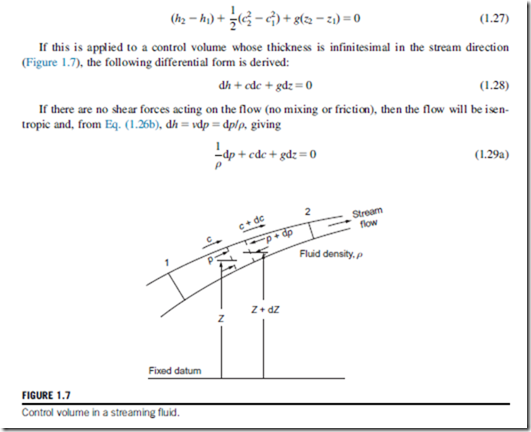
Consider the steady flow energy equation, Eq. (1.11). For adiabatic flow, with no work transfer,
Equation (1.29a) is often referred to as the one-dimensional form of Euler’s equation of motion. Integrating this equation in the stream direction we obtain
The thermodynamic properties of fluids
The three most familiar fluid properties are the pressure p, the temperature T and the density ρ. We also need to consider how other associated thermodynamic properties such as the internal energy u, the enthalpy h, the entropy s, and the specific heats Cp and Cv change during a flow process.
It is known from studies of statistical thermodynamics that in all fluid processes involving a change in pressure, an enormous number of molecular collisions take place in an extremely short interval which means that the fluid pressure rapidly adjusts to an equilibrium state. We can thus safely assume that all the properties listed above will follow the laws and state relations of classical equilibrium thermodynamics. We will also restrict ourselves to the following pure and homogenous substances: ideal gases, perfect gases, and steam.
Ideal gases
Air is a mixture of gases but, in the temperature range 160-2100 K, it can be regarded as a pure substance. Within this temperature range air obeys the ideal gas relationship:
The value of the gas constant R for any ideal gas is equal to a Universal Gas Constant R0 5 8314 J/kmol divided by the molecular weight of the gas. In this book many of the problems concern air so it is useful to evaluate a value for this gas mixture which has a molecular weight M 5 28.97 kg/kmol.
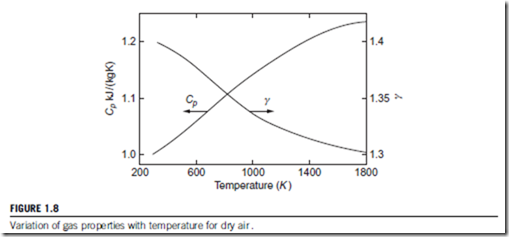
Over large temperature differences, air and many other common gases should be treated as semi-perfect gases. The variation in the values of Cp and γ for air are shown in Figure 1.8. Note that γ 5 Cp=Cv is the ratio of the specific heats, which is a particularly important parameter in compressible flow analysis (see Section 1.10).
Perfect gases
A perfect gas is an ideal gas for which Cp, Cv, and γ, are constants. Many real gases can be treated as perfect gases over a limited range of temperature and pressure. In the calculation of expansion or compression processes in turbomachines the normal practice is to use weighted mean values for Cp and γ according to the mean temperature of the process. Accordingly, in the problems in this book values have been selected for Cp and γ appropriate to the gas and the temperature range. For example, in air flow at temperatures close to ambient the value of γ is taken to be 1.4.
Note that the entropy change for a perfect gas undergoing any process can be calculated from the properties at the start and end of the process. Substituting dh 5 CpdT and pv 5 RT into Eq. (1.26b) gives:
Steam
Steam is the gaseous phase of water formed when pure water is boiled. When steam is in the two- phase region, where liquid and gaseous water coexist, it is known as wet steam. Steam turbines use the expansion of high-pressure steam to generate power. They typically operate close to or within the two-phase region, where the ideal gas law is highly inaccurate. No simple formulae apply and it is necessary to use tabulations of property values obtained by experiment and compiled as steam tables or steam charts to determine the effects of a change of state.
The thermodynamic properties of steam were the subject of many difficult investigations by groups of scientists and engineers over many years. An interesting summary of the methods used and the difficulties encountered are given in a paper by Harvey and Levelt Sengers (2001). The lat- est state-of-the-art account of the thermodynamic properties of water was adopted by the International Association for the Properties of Water and Steam (IAPWS) (Wagner and Pruss (2002)). The properties calculated from the current IAPWS standards for general and scientific use are distributed in a computer program by the National Institute of Standards and Technology (NIST) Standard Reference Data Program (Harvey, Peskin and Klein (2000)). These properties are also available via a free online calculator and in tabulated form (National Institute of Standards and Technology (2012)).
As well as steam tables the most immediate aid for performing calculations (although less accu- rate) is the Mollier diagram. This shows the enthalpy h (kJ/kg) plotted against entropy s (kJ/kg K) for various values of pressure p (MPa). A small, single-page Mollier chart is shown in Appendix E, but poster size charts can be obtained which, of course, enable greater accuracy.
Commonly used thermodynamic terms relevant to steam tables
i. Saturation curve
This is the boundary between the different phases on a property diagram. Saturated liquid refers to a state where all the water is in the liquid phase and saturated vapor refers to a state where all the water is in the gaseous phase. The two-phase region lies between the liquid and vapor saturation curves. Note that within the two-phase region temperature and pressure are no longer independent properties. For example, at 1 bar pressure, when water is boiling, all the liquid and gas is at 100oC.
ii. Quality or dryness fraction
This applies within the two-phase region and is the ratio of the vapor mass to the total mass of liquid and vapor. The value of any intensive property within the two-phase region is the mass weighted average of the values on the liquid and vapor saturation curves at the same pressure and temperature. Hence, the quality or dryness fraction can be used to specify the thermodynamic state of the steam.
For example, consider a quantity of wet steam at a state with dryness fraction x. The specific enthalpy of the steam at this state will be given by:
where hf is the enthalpy on the liquid saturation curve, and hg is the enthalpy on the vapor saturation curve, both at the same temperature and pressure of the wet steam. The above approach can be used for other intensive properties, such as u, v, s.
iii. Degree of superheat of steam.
When steam is heated at constant pressure in the gaseous phase it will be at a higher temperature than the corresponding saturation temperature. The temperature difference between the steam temperature and the saturation temperature at the same pressure is the degree of superheat.
iv. The Triple Point and the Critical Point.
The triple point for water is the unique temperature and pressure where all three phases coexist: ice, liquid water, and steam. The critical point is the state where the liquid and vapor saturation curves meet at the highest temperature and pressure possible in the two-phase region.
Related posts:
Incoming search terms:
- Application of momentum principle in turbo machinery
- moment of momentum equation in turbo
- aplication of the moment in fluid machineries
- Newtons second law of motion for turbomachine
- moment of momentum equation turbo machines
- moment of momendum equation
- momendum
- basic equation in turbomachinery
- appilication of momentum principle in turbo machinary
- state moment of momentum equation