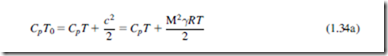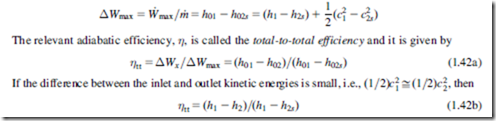Compressible flow relations for perfect gases
The Mach number of a flow is defined as the velocity divided by the local speed of sound. For a perfect gas, such as air over a limited temperature range, the Mach number can be written as
Whenever the Mach number in a flow exceeds about 0.3, the flow becomes compressible, and the fluid density can no longer be considered as constant. High power turbomachines require high flow rates and high blade speeds and this inevitably leads to compressible flow. The static and stag- nation quantities in the flow can be related using functions of the local Mach number and these are derived later.
Starting with the definition of stagnation enthalpy, h0 5 h 1 ð1=2Þc2, this can be rewritten for a perfect gas as
Figure 1.9 shows the relationship between stagnation and static conditions on a temperature- entropy diagram, in which the temperature differences have been exaggerated for clarity. This shows the relative stagnation properties as well as the absolute properties for a single point in a flow. Note that all of the conditions have the same entropy because the stagnation states are defined using an isentropic process. The pressures and temperatures are related using Eq. (1.36).
Choked flow
For subsonic flow, as flow speed and Mach number increase, the mass flow per unit area increases. This is because, from Eq. (1.8), the mass flow per unit area is m_ =A 5 ρc and as Mach number rises, the flow speed c increases more rapidly than the density ρ reduces. However, this is not true for supersonic flow and, above M 5 1, as flow speed and Mach number increase, the mass flow per unit area decreases. There is, therefore, a maximum mass flow per unit area which occurs at sonic conditions (M 5 1). This maximum can be readily observed by plotting out the nondimen- sional mass flow function given in Eq. (1.39) for a Mach number range from 0 to 2 using a fixed value of γ.
An important consequence of this is that the mass flow through any turbomachinery component reaches a maximum once M 5 1 across the section of minimum flow area. The flow is said to be choked and it is not possible to increase the mass flow further (without changing the inlet stagnation conditions). The section of minimum flow area is known as the throat and the size of the throat is a critical design parameter since it determines the maximum mass flow that can pass through a transonic turbomachine. Under choked conditions, because pressure waves in the flow travel at M 5 1, changes to the flow downstream of the throat cannot have any effect on the flow upstream of the throat.
Choking is considered in further detail for compressor and turbine blade rows within Sections
A large number of efficiency definitions are included in the literature of turbomachines and most workers in this field would agree there are too many. In this book only those considered to be important and useful are included.
Efficiency of turbines
Turbines are designed to convert the available energy in a flowing fluid into useful mechanical work delivered at the coupling of the output shaft. The efficiency of this process, the overall efficiency η0, is a performance factor of considerable interest to both designer and user of the turbine. Thus,
mechanical energy available at coupling of output shaft in unit time maximum energy difference possible for the fluid in unit time
Mechanical energy losses occur between the turbine rotor and the output shaft coupling as a result of the work done against friction at the bearings, glands, etc. The magnitude of this loss as a fraction of the total energy transferred to the rotor is difficult to estimate as it varies with the size and individual design of turbomachine. For small machines (several kilowatts) it may amount to 5% or more, but for medium and large machines this loss ratio may become as little as 1%. A detailed consideration of the mechanical losses in turbomachines is beyond the scope of this book and is not pursued further.
The ideal work is slightly more complicated as it depends on how the ideal process is defined. The process that gives maximum work will always be an isentropic expansion, but the question is one of how to define the exit state of the ideal process relative to the actual process. In the following paragraphs the different definitions are discussed in terms of to what type of turbine they are applied.
Steam and gas turbines
Figure 1.10(a) shows a simplified Mollier diagram representing the expansion process through an adiabatic turbine. Line 1-2 represents the actual expansion and line 1-2s the ideal or reversible expansion. The fluid velocities at entry to and exit from a turbine may be quite high and the corresponding kinetic energies significant. On the other hand, for a compressible fluid the potential energy terms are usually negligible. Hence, the actual turbine rotor specific work is
There are two main ways of expressing the isentropic efficiency, the choice of definition depending largely upon whether the exit kinetic energy is usefully employed or is wasted. If the exhaust kinetic energy is useful, then the ideal expansion is to the same stagnation (or total) pressure as the actual process. The ideal work output is, therefore, that obtained between state points 01 and 02s,
An example where the exhaust kinetic energy is not wasted is from the last stage of an aircraft gas turbine where it contributes to the jet propulsive thrust. Likewise, the exit kinetic energy from one stage of a multistage turbine where it can be used in the following stage provides another example.
If, instead, the exhaust kinetic energy cannot be usefully employed and is entirely wasted, the ideal expansion is to the same static pressure as the actual process with zero exit kinetic energy. The ideal work output in this case is that obtained between state points 01 and 2s:
A situation where the outlet kinetic energy is wasted is a turbine exhausting directly to the surroundings rather than through a diffuser. For example, auxiliary turbines used in rockets often have no exhaust diffusers because the disadvantages of increased mass and space utilization are greater than the extra propellant required as a result of reduced turbine efficiency.
By comparing Eqs. (1.42) and (1.43) it is clear that the total-to-static efficiency will always be lower than the total-to-total efficiency. The total-to-total efficiency relates to the internal losses (entropy creation) within the turbine, whereas the total-to-static efficiency relates to the internal losses plus the wasted kinetic energy.
EXAMPLE 1.4
A steam turbine receives 10 kg/s of superheated steam at 20 bar and 350oC which then expands through the turbine to a pressure of 0.3 bar and a dryness fraction of 0.95. Neglecting any changes in kinetic energy, determine
a. the change in enthalpy of the steam in its passage through the turbine
b. the increase in entropy of the steam
c. the total-to-total efficiency of the turbine.
d. the power output of the turbine
Solution
A small Mollier diagram for steam is shown in Appendix E. This can be used to verify the enthalpy and entropy values for the expansion given below.
Hydraulic turbines
The turbine hydraulic efficiency is a form of the total-to-total efficiency expressed previously. The steady flow energy equation (Eq. 1.11) can be written in differential form for an adiabatic turbine as
Efficiency of compressors and pumps
The isentropic efficiency, ηc, of a compressor or the hydraulic efficiency of a pump, ηh, is broadly defined as
The power input to the rotor (or impeller) is always less than the power supplied at the coupling because of external energy losses in the bearings, glands, etc. Thus, the overall efficiency of the compressor or pump is
Figure 1.10(b) shows a Mollier diagram on which the actual compression process is represented by the state change 1-2 and the corresponding ideal process by 1-2s. For an adiabatic compressor in which potential energy changes are negligible, the most meaningful efficiency is the total-to- total efficiency, which can be written as