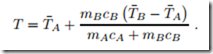Example: Equilibration of Temperature
We apply the first law to the situation depicted in Fig. 2.6. Two bodies A and B that are initially at different temperatures T¯A and T¯B , respectively, are brought into thermal contact. After a sufficiently long time, we find that both bodies have assumed the common temperature T .
For this problem, kinetic energy is zero, and potential energy does not change. When the system [A + B] is adiabatically enclosed (Q˙ = 0), and no work is done (W˙ = 0), the first law of thermodynamics simply states that the energy of the system remains constant,
Thus, the energy of the end state is equal to the initial energy, Uend = Uinit.
For simple incompressible solids the internal energy is given by4 U = mcT , where c denotes the average specific heat (assumed to be a constant) and m is the mass. The internal energy of the system consisting of the two bodies is initially
To emphasize that the first law does not automatically give equal final tem- peratures for the two bodies, we write Uend = mAcATA + mB cB TB with different final temperatures TA and TB . We solve for TA,
and see that there are infinitely many solutions for the final temperatures (TA, TB ) that fulfill the first law: conservation of energy alone is not sufficient to determine the final equilibrium state.
However, our experience, laid down in the zeroth law, tells us that the final temperatures agree: TA = TB = T . We find the final temperature as the weighted average of the two initial temperatures,
with the weights given by the thermal masses mAcA, mB cB . We shall later employ the second law to find the same result.
As discussed, a thermometer utilizes the equilibration of temperature. The act of measurement should not affect the result. To study the relevant condition, let body B be the thermometer, used to measure the temperature of body A. The final temperature T of body and thermometer can be written in the alternative form
The measured temperature T is close to the initial temperature T¯A of body A when mB cB « mAcA. It follows that a thermometer should have considerably smaller thermal mass mc than the body whose temperature is to be measured.