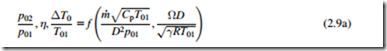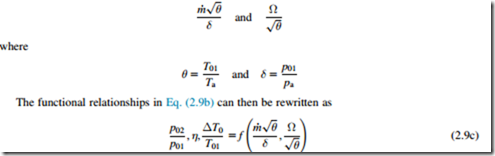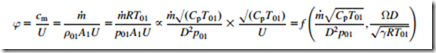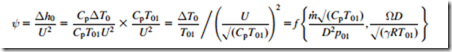Dimensional Analysis,Similitude:Compressible flow analysis

Compressible flow analysis

The application of dimensional analysis to compressible flow increases, not unexpectedly, the complexity of the functional relationships obtained in comparison with those already found for incompressible fluids. Even if the fluid is regarded as a perfect gas, in addition to the previously used fluid properties, two further characteristics are required; these are a01, the stagnation speed of sound at entry to the machine, and γ, the ratio of specific heats Cp/Cν. In the following analysis, the compressible fluids under discussion are either perfect gases or dry vapors approximating in behavior to a perfect gas.

Another choice of variables is preferred when appreciable density changes occur across the machine. Instead of volume flow rate Q, the mass flow rate m_ is used; likewise for the head change H, the isentropic stagnation enthalpy change Δh0s is employed. The choice of this last variable is a significant one for, in an ideal and adiabatic process, Δh0s is equal to the work done per unit mass of fluid. Since heat transfer from the casings of turbomachines is, in general, of negligible magnitude compared with the flux of energy through the machine, temperature on its own may be safely excluded as a fluid variable. However, temperature is an easily observable characteristic and, for a perfect gas, can be easily introduced by means of the equation of state, p/ρ 5 RT.

The performance parameters Δh0s, η, and P, for a turbomachine handling a compressible flow, can be expressed functionally as

Because ρ0 and a0 change through a turbomachine, the values of these fluid variables are selected at inlet, denoted by subscript 1. Equation (2.5) expresses three separate functional relation-ships, each of which consists of eight variables. Again, selecting ρ01, Ω, and D as common factors, each of these three relationships may be reduced to five dimensionless groups:

For a machine handling a perfect gas, a different set of functional relationships is often more useful. These may be found either by selecting the appropriate variables for a perfect gas and work- ing through again from first principles or, by means of some rather straightforward transformations, rewriting Eq. (2.6b) to give more suitable groups. The latter procedure is preferred here as it pro- vides a useful exercise. As an example, consider an adiabatic compressor handling a perfect gas. The isentropic stagnation enthalpy rise can be written as Cp(T02s 2 T01) for a perfect gas. As shown in Chapter 1, the isentropic relationship between temperature and pressure is given by

A key advantage of Eq. (2.8) over Eq. (2.6b) is that the nondimensional groups are in terms of inlet and exit stagnation temperatures and pressures, which are parameters that are readily measured for a turbomachine. For a machine handling a single gas, γ can be dropped as an independent variable. If, in addition, the machine operates only at high Reynolds numbers (or over a small speed range), Re can also be dropped. Equation (2.8) can then be written with just two nondimensional groups on the right-hand side:

In this equation, the nondimensional group, is often referred to as the flow capacity, introduced in Section 1.10 of Chapter 1. This is the most widely used form of nondimensional mass flow, although the forms in Eqs (2.6b) and (2.8) are also valid. For machines of a known size and fixed working fluid, it has become customary, in industry at least, to delete γ, R, Cp, and D from Eq. (2.9a) and similar expressions. Under these conditions, Eq. (2.9a) becomes

Note that by omitting the diameter D and gas constant R, the independent variables on the right-hand side of Eq. (2.9b) are no longer dimensionless.

For a given turbomachine, Eq. (2.9b) is sometimes expressed in terms of corrected flow and corrected speed. These are the mass flow and speed that would be measured if the machine was operating at standard sea-level atmospheric pressure and temperature, pa and Ta.

The corrected mass flow and corrected speed are defined as

Note that the parameters on the right-hand side are no longer nondimensional. The units of the first parameter are kg/s and that of the second are rad/s. To nondimensionalize these parameters, they can be normalized by their values at the design point.

Equations (2.9a-c) show that two variables are required to fix the operating point of a compressible flow machine. This compares to the one variable needed to fix the operating point of an incompressible flow machine, Eqs. (2.3a-c). In all cases, for dynamic similarity, the streamline pattern relative to the blades must be geometrically similar. In an incompressible flow machine, it is enough just to fix the relative inlet angle to the blades (via the flow coefficient). In a compress- ible flow machine, the streamline pattern within the blade rows also depends on the variation of density through the blade passages. Therefore, a second parameter is needed to fix the flow Mach numbers and thus fix the variation of density.

Similarly to the incompressible case, the performance parameters, p02/p01, η, and ΔT0/T01 are not entirely independent and it is straightforward to write an equation relating the three. For a compressor, the isentropic efficiency is defined in Chapter 1 and can be written as

Flow coefficient and stage loading

In compressible flow machines, the flow coefficient, Φ, is an important parameter for design and analysis. It is defined in the same way as given earlier for incompressible machines, i.e., Φ 5 cm/U, where U is the mean blade speed and cm the average meridional velocity. However, in the compressible case, the flow coefficient alone cannot be used to fix the operating condition of a machine. This is because the flow coefficient is also a function of the nondimensional parameters given in Eq. (2.9a). It is straightforward to show this via the following algebraic manipulation:

Note that the nondimensional mass flow, is distinct from a flow coefficient because it does not involve the blade speed.

The stage loading, ψ, is another key design parameter for all nonhydraulic turbomachines. It is defined as

This parameter is similar in form to the head coefficient ψ used in hydraulic machines (Eq. (2.2a)), but there are subtle differences. Most importantly, stage loading is a nondimensional form of the actual specific stagnation enthalpy change, whereas the head coefficient is a nondimensional measure of the maximum, or isentropic, work that a hydraulic machine can achieve. Note that the stage loading can be related to the nondimensional parameters in Eq. (2.9a) as follows:

Thus, the stage loading is also fixed once both the nondimensional mass flow and the nondimensional blade speed (or blade Mach number) are fixed. In many cases, the stage loading is used in place of the power coefficient ΔT0/T0 given in Eq. (2.9a).

Heating Swimming Pools:Oil-Fired Pool Heaters

MOTORS:THE NAMEPLATE

Radiators, Convectors, and Unit Heaters:Sizing Radiators

Ideal gas laws:Boyle’s law,Charles’ law,The pressure law,Dalton’s law of partial pressure,Characteri...

Dimensional Analysis,Similitude: Performance characteristics for high-speed machines Compressors and...

Radiant Heating:Installing a Hydronic Radiant Floor Heating System (PEX Tubing)

Work and Heat.

Radiators, Convectors, and Unit Heaters:Steam and Hot-Water Baseboard Heaters

Ventilation Principles:Stationary-Head Ventilators