Dimensional Analysis: Similitude
Dimensional analysis and performance laws
The widest comprehension of the general behavior of all turbomachines is, without doubt, obtained from dimensional analysis. This is the formal procedure whereby the group of variables representing some physical situation is reduced to a smaller number of dimensionless groups. When the number of independent variables is not too great, dimensional analysis enables experimental relations between variables to be found with the greatest economy of effort. Dimensional analysis applied to turbomachines has two further important uses: (a) prediction of a prototype’s performance from tests conducted on a scale model (similitude), and (b) determination of the most suitable type of machine, on the basis of maximum efficiency, for a specified range of head, speed, and flow rate. Several methods of constructing nondimensional groups have been described by Douglas, Gasiorek, and Swaffield (1995) and Shames (1992), among other authors. The subject of dimensional analysis was made simple and much more interesting by Taylor (1974) in his comprehensive account of the subject and this approach is the one adopted in this book.
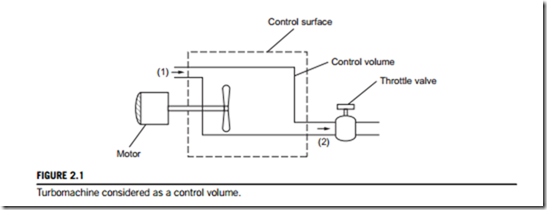
Adopting the simple approach of elementary thermodynamics, a control surface of fixed shape, position, and orientation is drawn around the turbomachine (Figure 2.1). Across this boundary, fluid flows steadily, entering at station 1 and leaving at station 2. As well as the flow of fluid, there is a flow of work across the control surface, transmitted by the shaft either to or from the machine. All details of the flow within the machine can be ignored and only externally observed features such as shaft speed, flow rate, torque, and change in fluid properties across the machine need be considered. To be specific, let the turbomachine be a pump (although the analysis could apply to other classes of turbomachine) driven by an electric motor. The speed of rotation Ω can be adjusted by altering the current to the motor; the volume flow rate Q can be independently adjusted by means of a throttle valve. For fixed values of the set Q and Ω, all other variables, such as torque, τ, and head, H, are thereby established. The choice of Q and Ω as control variables is clearly arbitrary and any other pair of independent variables such as τ and H could equally well have been chosen.
The important point to recognize is that there are, for this pump, two control variables.
If the fluid flowing is changed for another of different density, ρ and viscosity, μ, the performance of the machine will be affected. Note also that, for a turbomachine handling compressible fluids, other fluid properties are important and these are discussed later.
So far we have considered only one particular turbomachine, namely a pump of a given size. To extend the range of this discussion, the effect of the geometric variables on the performance must now be included. The size of machine is characterized by the impeller diameter, D, the shape can be expressed by a number of length ratios, l1/D, l2/D, etc., and the surface finish can be characterized by a representative roughness length, e.