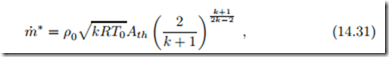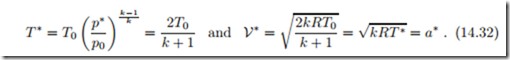Converging Nozzle
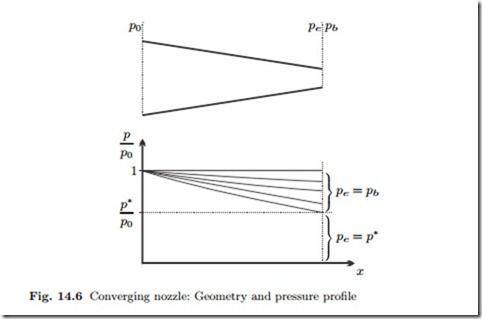
As the back pressure pb is lowered a bit, the flow develops. The cross section A is decreasing along the nozzle coordinate x, see Fig. 14.6. According to Fig. 14.4, the flow function is hill-shaped, and the nozzle feed state is on the right foot of that hill, at p = p0, ψ = 0. Since Aψ p is constant, for
decreasing cross section A the flow function must grow, i.e., go uphill. The flow function grows along x, and reaches its largest value in the smallest cross section Ath, the throat of the nozzle, which is at the end of the converging nozzle. As ψ grows along the nozzle coordinate, the pressure decreases, until it assumes the pressure pe = pb in the end cross section of the nozzle. Further decrease of the back pressure leads to lower pressures along the nozzle, and larger values of the flow function.
When the back pressure pb assumes the critical value p∗, the flow function in the exit is at its maximum ψ∗. No further growth of ψ is possible when the back pressure is lowered further. Thus, the exit state remains at ψe = ψ∗ and pe = p∗, even when the back pressure is lowered below p∗. Figure 14.6 visualizes this behavior.
When the pressure p∗ is reached in the nozzle throat, one speaks of choked flow. Indeed, under this condition, the mass flow obtains a maximum value,
where Ath is the cross section at the nozzle end. No further increase of the mass flow through the nozzle is possible. To understand this behavior, we determine temperature and velocity in the exit at choked conditions. From the adiabatic relation and (14.26, 14.29) we find
Thus, for choked flow, the exit speed is just the local speed of sound, a∗. We recall that the speed of sound is the velocity of a pressure disturbance. When the back pressure is lowered, the information on the pressure change travels with the speed of sound relative to the gas. Since the gas leaves with just the same speed, the information on pressure change is not transmitted into the nozzle, and no changes can occur inside, the exit velocity and the mass flow are limited.
With pb < p∗, a pressure discontinuity occurs at the nozzle exit, which contributes to thrust for the airplane or rocket. The exhaust expands outside the nozzle to the back pressure, and accelerates, and this expansion is some- what irreversible, more so with bigger pressure differences.2 Most commercial airplanes have converging nozzles and subsonic outflow, to reduce noise.