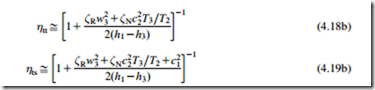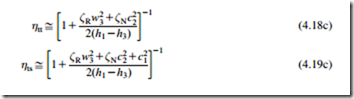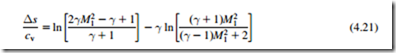Stage losses and efficiency
In Chapter 1, various definitions of efficiency for complete turbomachines were given. For a turbine stage, the total-to-total efficiency is
The slope of a constant pressure line on a Mollier diagram is (@h/@s)p 5 T, obtained from Eq. (1.28). Thus, for a finite change of enthalpy in a constant pressure process, ΔhDTΔs (and Δh0DT0Δs). The total-to-total efficiency can therefore be rewritten as
As shown by Figure 4.4, the entropy change across the whole stage, s3 2 s3ss, is the sum of the entropy increase across the nozzle row, s2 2 s2s 5 s3s 2 s3ss, and the entropy increase across the rotor row, s3 2 s3s. These increases in entropy represent the cumulative effects of irreversibility through the stator and rotor. Nondimensional enthalpy “loss” coefficients can be defined in terms of the exit kinetic energy from each blade row (Eq. (3.7)). For the nozzle row,
128 CHAPTER 4 Axial-Flow Turbines: Mean-Line Analysis and Design Hence, the entropy change through the stator in terms of the enthalpy loss coefficient is
Equations (4.18a) and (4.19a) are applicable to all turbine stages. For a repeating (or normal) stage, the inlet and exit flow conditions (absolute velocity and flow angle) are identical, i.e., c1 5 c3 and α1 5 α3. In this case, h01 2 h03 5 h1 2 h3. If, in addition, the interstage absolute Mach number is fairly low, T03=T3D1, the total-to-total efficiency and the total-to-static efficiency can be written as
For incompressible flow turbines, and other cases where the static temperature drop through the rotor is not large, the temperature ratio T3/T2 can be set equal to unity resulting in the more convenient approximations:
So that estimates can be made of the efficiency of a proposed turbine stage, as part of the pre- liminary design process, some means of determining the loss coefficients, ζN and ζR, are required.
Several methods for doing this are available with varying degrees of complexity. The blade row method proposed by Soderberg (1949) and reported by Horlock (1966), although old, is still useful despite its simplicity, see Eq. (3.46). Ainley and Mathieson (1951) developed a semiempirical method based on profile loss coefficient data for nozzle blades (with 100% expansion) and impulse blades (with 0% expansion), see Eq. (3.45). Full details of both these methods are given in Section 3.6.
It should be remembered that loss coefficients based on cascade testing or 2D computational fluid dynamics (CFD) represent only the 2D loss of the aerofoils and in a real turbine, various 3D effects also contribute to the loss. These 3D effects, described in further detail below, include the tip leakage jet, the mixing of any coolant flows, and the secondary flows on the turbine end walls. These effects are significant and can contribute more than 50% of the total losses.
Further preliminary methods of predicting the efficiency of axial-flow turbines have been devised, such as those of Craig and Cox (1971), Kacker and Okapuu (1982), and Wilson (1987). Also various proprietary methods are used within industry that are generally semiempirical methods based on previous test results for turbine stages of a similar design. In addition, CFD can be used to estimate efficiency. However, although CFD can often accurately predict trends in efficiency, absolute performance levels are elusive even with the latest 3D methods. In addition, CFD can only be applied once detailed turbine rotor and stator geometries have been created. It is therefore more applicable later in the design process, see Chapter 6. Advanced computational methods have not yet replaced preliminary design methods and these are still essential to converge as closely as possible to an optimum configuration before carrying out detailed design refinements using CFD.
Turbine loss sources
As stated in Chapter 1, wherever there is irreversible entropy creation within the flow path of a turbomachine, there is a loss in the available work. A loss source is therefore any flow feature that leads to entropy creation. Entropy is created by irreversible processes that involve viscous friction, mixing between flows of different properties, heat transfer across a finite temperature difference, or nonequilibrium changes like shock waves. In a turbine stage, there are numerous loss sources and they can each be quantified by the entropy they generate. The total loss is then the cumulative sum of the entropy increases, which can be used to determine a single blade row loss coefficient, as used in mean-line analysis, and applied in Eqs (4.16)-(4.19) above. However, in many cases it is very difficult to determine the entropy generation associated with a particular loss source, and los s coefficients are generally based on values derived from testing a similar machine combined with correlations.
A detailed description of all of the different loss mechanisms in turbomachinery is given by Denton (1993), and this reference is strongly recommended. Here the aim is to give a brief over- view of the principal loss sources in turbines and their relative importance.
The losses in a turbine can be categorized as 2D or 3D. The 2D loss sources are those that would be present in a cascade test of a turbine blade row with infinite span (i.e., no endwall effects). The 3D losses are the additional losses that arise when the turbine stage is operating in a realistic rotating arrangement.
130 CHAPTER 4 Axial-Flow Turbines: Mean-Line Analysis and Design
2D loss sources are made up of (a) the blade boundary layers, (b) trailing edge mixing, (c) flow separation, and (d) shock waves.
The loss in the blade boundary layers can be thought of as lost work expended against viscous shear within the boundary layers. Its magnitude depends on the development of the boundary layer and, in particular, on the blade surface pressure distribution and where transition from laminar to turbulent flow occurs. Boundary layer loss typically accounts for over 50% of the 2D loss in sub- sonic turbines. For incompressible flow, Denton (1993) shows that the total loss in a boundary layer can be determined using
The trailing edge mixing loss is the loss that arises from the mixing of the suction surface and pressure surface boundary layers with the region of flow just behind the trailing edge. This loss is significant, typically about 35% of the total 2D loss in subsonic turbines, and rising to around 50% in supersonic cases, see Figure 3.26. Note that for incompressible cases, the combined boundary layer loss and trailing edge loss can be accounted for by the wake momentum thickness, θ2, as shown in Eq. (3.38),
Combining this with Eq. (4.20) shows that the ratio of loss in a boundary layer to the total loss within the wake after mixing is given by δe/2θ2.
Flow separation loss exists when the boundary layer detaches from the blade surface and a large region of reduced kinetic energy flow forms downstream. This loss is difficult to quantify, but a well-designed turbine should never exhibit large-scale 2D flow separation, so it can generally be neglected. Separation close to the trailing edge is included in the trailing edge mixing loss.
Shock loss occurs when the turbine blade passage is choked and the exit Mach number is above about 0.9. The loss caused by shock waves in a turbine passage is not as great as might be expected. For a normal shock wave, with a preshock Mach number, M1, it can be shown, see National Advisory Committee for Aeronautics Report 1135 (1953), that the entropy generation is given by
If the above is expanded as a power series, it is found that the entropy creation varies approximately as the cube of ðM2 2 1Þ, which is relatively small up to Mach numbers of about 1.4. In turbine passages the shock waves are usually oblique, reducing the losses further. As shown in Figure 3.26, shock loss accounts for about 30% or less of the total 2D loss above an exit Mach number of 1.
3D loss sources can be separated into (a) tip leakage flows, (b) endwall (or secondary) flows, and (c) coolant flows.
In all turbomachines, a clearance gap exists between the rotating blades and the stationary casing. Tip leakage is the passage of flow from the pressure surface to the suction surface of the blade through this clearance gap. The leakage flow leads to a reduction in the work done by a turbine rotor because the mass flow rate through the blade passage is reduced. It also leads to a loss in effi- ciency. First, the leakage flow increases its entropy through viscous effects and mixing as it passes through the leakage path above the blade tip. Second, when the leakage flow emerges at the suction side it mixes with the main flow, creating a further entropy rise. These losses are demonstrated in Bindon (1989) and various models exist to determine the leakage mass flow rate and the loss gener- ated. Tip leakage loss rises rapidly with the size of clearance gap and typically a 1% increase of clearance gap to blade height will incur a loss of 2-3% of efficiency. It is, therefore, more detrimental in small turbine stages that have relatively large clearance gaps. Note that stator rows also suffer from leakage losses if they have clearance flow paths.
Endwall loss is a large, complex subject and an area of active research. It encompasses all of the loss arising on the hub and casing surfaces, both inside and outside of the blade rows. Endwall loss is very difficult to isolate and predict, but typically it accounts for about 30% of the total loss in a turbine stage, see Denton (1993). The flow close to the annulus walls is determined by secondary flows in the blade passage, which are driven by the incoming endwall boundary layers and the turning in the blade passage, see Chapter 6.
Loss from coolant flows is only applicable to high-temperature cooled gas turbine stages, see Section 4.14. The overall effect must be considered in terms of the thermodynamics of the complete gas turbine system. Cooling is applied to increase the turbine entry temperature, which raises the cycle efficiency and work output. However, the cooling process itself is highly irreversible. Entropy is cre- ated by heat transfer from the mainstream flow, by the passage of the coolant through convoluted pas- sages and by the mixing of the coolant with the mainstream flow. The last of these processes has a significant impact on the turbine stage efficiency. The coolant flow is injected into the blade passages at an angle through holes or slots and has quite different stagnation temperature and pressure to the mainstream flow. Various models have been developed that enable this mixing loss to be quantified, see Denton (1993), but accurately predicting the efficiency impact is still challenging.
Steam turbines
The above efficiency analysis and discussion of loss sources also applies to steam turbines. The main difference to keep in mind for steam turbines is that the working fluid cannot be approxi- mated as an ideal gas and steam tables or a Mollier chart for steam (Appendix E) have to be used. As a result, the changes in properties through a steam turbine stage can be much greater than through a gas turbine stage. Equations (4.18a) and (4.19a) are still valid for a steam turbine stage, and for modern designs, typically 88% , ηtt , 93%, but in a multistage turbine the loss coefficients can vary significantly between the front and rear stages, see McCloskey (2003, chap. 8). In cases where only the inlet and exit conditions to a multistage steam turbine are known it is more appro- priate to use the overall isentropic efficiency. This can be related to an equivalent small-stage (or polytropic) efficiency, using the reheat factor, as shown in Eq. (1.56),
where h01 is the stagnation enthalpy of the steam at the turbine inlet temperature and pressure, h02 is the stagnation enthalpy of the steam at the exit temperature and pressure, and h02s is the stagnation enthalpy of the steam at the exit pressure and the inlet entropy.
In addition to the loss sources described previously, steam turbines suffer additional losses due to moisture in the working fluid. Water droplets form when steam crosses the saturation line into the two- phase region on the steam chart, see Appendix E. For a steam turbine in a power station, the overall efficiency typically drops by about 1% for every 1% of wetness in the final stages. This has led to tur- bine designs in which moisture levels in the exhaust are limited to around 10% (Hesketh & Walker, 2005). Steam turbines also suffer particularly from leakage losses and surface roughness effects. There are multiple leakage paths in steam turbines, such as over the rotor tips, the stator shrouds, and through various seals. Some surface roughness arises in manufacture, but it is rapidly worsened by the particle erosion and blade surface deposits that can occur when operating with steam. However, since the oper- ating temperatures are lower than gas turbines, steam turbines do not have cooled blades and, therefore, avoid the additional losses and complexity required by blade cooling.
EXAMPLE 4.1
A low-pressure steam turbine within a power station has an entry temperature of 450oC and an entry pressure of 30 bar. At exit from the turbine, the condenser pressure is 0.06 bar and due to the effects of moisture, the turbine isentropic efficiency is given by ηt 5 0:9 2 y, where y is the wetness fraction of the steam at turbine exit (and y 5 1 2 x, where x is the dryness fraction).
1. Find the net work output from the turbine per kg of steam and determine the turbine polytro pic efficiency assuming a reheat factor of 1.02.
2. The turbine consists of repeating stages designed with zero reaction, a flow coefficient of 0.8 and axial flow at inlet to each stage. If it rotates at 3000 rpm and has a mean radius of 0.9 m, determine the number of stages, the absolute flow angle at nozzle exit, and the relative angle at rotor inlet.
Use the following table of properties for water and steam: