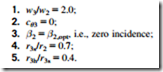Radial-Flow Gas Turbines:Significance and application of specific speed.

Significance and application of specific speed

The concept of specific speed, Ωs, has already been discussed in Chapter 2 and some applications of it have been made already. Specific speed is extensively used to describe turbomachinery operating requirements in terms of shaft speed, volume flow rate, and ideal specific work (alternatively, power developed is used instead of specific work). Originally, specific speed was applied almost exclusively to incompressible flow machines as a tool in the selection of the optimum type and size of unit. Its application to units handling compressible fluids was somewhat inhibited, due, it would appear, to the fact that volume flow rate changes through the machine, which raised the awkward question of which flow rate should be used in the specific speed definition. According to Balje (1981), the significant volume flow rate that should be used for turbines is that in the rotor exit, Q3. This has now been widely adopted by many authorities.

Wood (1963) found it useful to factorize the basic definition of the specific speed equation, Eq. (2.14a), in terms of the geometry and flow conditions within the radial-inflow turbine. Adopting the nondimensional form of specific speed, to avoid ambiguities,

where Ω is in rad/s, Q3 is in m3/s, and the isentropic total-to-total enthalpy drop Δh0s (from turbine inlet to exhaust) is in joules per kilogram (i.e., square meters per second squared).

For the 90o IFR turbine, writing U2 5 0.5ΩD2 and Δh0s 5 ð1=2Þc2, Eq. (8.46) can be factorized as follows:

For the ideal 90o IFR turbine and with cθ2 5 U2, it was shown earlier that the blade speed to spouting velocity ratio, U2=c0 5 pﬃ2ﬃ 5 0:707. Substituting this value into Eq. (8.47a),

that is, specific speed is directly proportional to the square root of the volumetric flow coefficient.

To obtain some physical significance from Eqs (8.46) and (8.47b), define a rotor disc areaAd 5 πD2=4 and assume a uniform axial rotor exit velocity c3 so that Q3 5 A3c3, as

In an early study of IFR turbine design for maximum efficiency, Rohlik (1968) specified that the ratio of the rotor shroud diameter to rotor inlet diameter should be limited to a maximum value of 0.7 to avoid excessive shroud curvature and that the exit hub-shroud tip ratio was limited to a minimum of 0.4 to avoid excess hub blade blockage and loss. Using this as data, an upper limit for A3/Ad can be found,

Figure 8.10 shows the relationship between Ωs, the exhaust energy factor (c3/c0)2, and the area ratio A3/Ad based upon Eq. (8.47c). According to Wood (1963), the limits for the exhaust energy factor in gas turbine practice are 0.04 , (c3/c0)2 , 0.30, the lower value being apparently a flow stability limit.

The numerical value of specific speed provides a general index of flow capacity relative to work output. Low values of Ωs are associated with relatively small flow passage areas and high values with relatively large flow passage areas. Specific speed has also been widely used as a general indication of achievable efficiency. Figure 8.11 presents a broad correlation of maximum efficiencies for hydraulic and compressible fluid turbines as functions of specific speed. These efficiencies apply to favorable design conditions with high values of flow Reynolds number, efficient diffusers, and low leakage losses at the blade tips. It is seen that over a limited range of specific speed the best radial-flow turbines match the best axial-flow turbine efficiency, but from Ωs 5 0.03-10 no other form of turbine handling compressible fluids can exceed the peak performance capability of the axial turbine.

Over the fairly limited range of specific speed (0.3 , Ωs , 1.0) that the IFR turbine can produce a high efficiency, it is difficult to find a decisive performance advantage in favor of either the

axial-flow turbine or the radial-flow turbine. New methods of fabrication enable the blades of small axial-flow turbines to be cast integrally with the rotor so that both types of turbine can operate at about the same blade tip speed. Wood (1963) compared the relative merits of axial and radial gas turbines at some length. In general, although weight, bulk, and diameter are greater for radial than axial turbines, the differences are not so large and mechanical design compatibility can reverse the difference in a complete gas turbine power plant. The NASA nuclear Brayton cycle space power studies were all made with 90o IFR turbines rather than with axial-flow turbines.

The design problems of a small axial-flow turbine were discussed by Dunham and Panton (1973), who studied the cold performance measurements made on a single-shaft turbine of 13 cm diameter, about the same size as the IFR turbines tested by NASA. Tests had been performed with four rotors to try to determine the effects of aspect ratio, trailing edge thickness, Reynolds number, and tip clearance. One turbine build achieved a total-to-total efficiency of 90%, about equal to that of the best IFR turbine. However, because of the much higher outlet velocity, the total-to-static efficiency of the axial turbine gave a less satisfactory value (84%) than the IFR type which could be decisive in some applications. They also confirmed that the axial turbine tip clearance was comparatively large, losing 2% efficiency for every 1% increase in clearance. The tests illustrated one major design problem of a small axial turbine that was the extreme thinness of the blade trailing edges needed to achieve the efficiencies stated.

Optimum design selection of 90 IFR turbines

Rohlik (1968) has examined analytically the performance of 90o IFR turbines to determine optimum design geometry for various applications as characterized by specific speed. His procedure, which extends an earlier treatment of Wood (1963), was used to determine the design point losses and corresponding efficiencies for various combinations of nozzle exit flow angle, α2, rotor diameter ratio, D2/D3, and rotor-blade entry height to exit diameter ratio, b2/D3. The losses taken into account in the calculations are those associated with

1. nozzle blade row boundary layers;

2. rotor passage boundary layers;

3. rotor-blade tip clearance;

4. disc windage (on the back surface of the rotor);

5. kinetic energy loss at exit.

A mean flow path analysis was used and the passage losses were based upon the data of Stewart et al. (1960). The main constraints in the analysis were

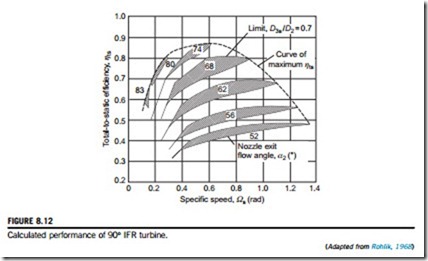
Figure 8.12 shows the variation in total-to-static efficiency with specific speed (Ωs) for a selection of nozzle exit flow angles, α2. For each value of α2 a hatched area is drawn, inside of which the various diameter ratios are varied. The envelope of maximum ηts is bounded by the constraints D3h/D3s 5 0.4 in all cases and D3s/D2 5 0.7 for Ωs $ 0.58 in these hatched regions. This envelope is the optimum

geometry curve and has a peak ηts of 0.87 at Ωs 5 0.58 rad. An interesting comparison is made by Rohlik with the experimental results obtained by Kofskey and Wasserbauer (1966) on a single 90o IFR turbine rotor operated with several nozzle blade row configurations. The peak value of ηts from this experimental investigation also turned out to be 0.87 at a slightly higher specific speed, Ωs 5 0.64 rad.

The distribution of losses for optimum geometry over the specific speed range is shown in Figure 8.13. The way the loss distributions change is a result of the changing ratio of flow to specific work. At low Ωs all friction losses are relatively large because of the high ratios of surface area to flow area. At high Ωs the high velocities at turbine exit cause the kinetic energy leaving loss to predominate.

Figure 8.14 shows several meridional plane sections at three values of specific speed corresponding to the curve of maximum total-to-static efficiency. The ratio of nozzle exit height-rotor diameter, b2/D2, is shown in Figure 8.15, the general rise of this ratio with increasing Ωs reflecting the increase in nozzle flow area4 accompanying the larger flow rates of higher specific speed. Figure 8.15 also shows the variation of U2/c0 with Ωs along the curve of maximum total-to-static efficiency.

Heating Fuels:Comparing Heating Fuel Costs

Summary of Hydronic Systems

Service valves and gauges:Service gauge manifold

Ventilation and Exhaust Fans:Series and Parallel Fan Operation

Ventilation and Exhaust Fans:Fan Selection

Hydronic Heating Systems:Hot-Water Boilers

Hot-Water Heating Systems - CIRCULATING PUMPS

Furnace Fundamentals:Classifying Furnaces

Pipework and oil traps:Installation principles