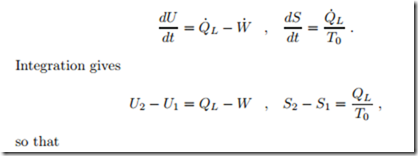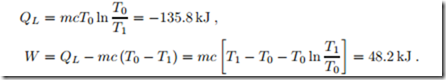Examples
Entropy Generation in Cooling
A 2 kg block of copper at T1 = 250 ◦C equilibrates with the environment at T0 = 20 ◦C through heat transfer. The left part of Fig. 5.7 shows a sketch of the process, where the system boundary is chosen such that heat is transferred at the environmental temperature T0. Copper can be considered as an incompressible solid with constant specific heat c = 0.4 kJ , specific internal energy u = c (T − T0), and specific entropy s = c ln T . We compute the amount of heat transferred into the environment, and the total entropy generated.
The first and second law for this process read
Since entropy is generated, an irreversible loss is associated with the process. The entropy generating process is heat transfer over the finite temperature difference between copper block and environment.
Work Generation in Cooling
In the this example we determine the amount of work that could have been obtained if the heat was not just transferred, but used to drive a heat engine. We consider the same block of copper as before, but now the heat is used to drive a Carnot engine in contact with the environment, as shown in the right part of Fig. 5.7. In this case, there is no entropy generation, since the Carnot engine is fully reversible. Thus, the first and second laws read (system boundaries include the Carnot engine)
A temperature difference can be used to drive a heat engine. If heat is just transferred over a finite temperature difference, entropy is created, and the opportunity to provide work is lost. In this example about 26% of the heat leaving the copper (QH = 184 kJ) could be converted to work in the best case. Note that W = T0Sgen, where Sgen is the entropy generation in case that no work is produced as computed in the previous section.
Perpetual Motion Engines
We consider some perpetual motion engines.
(a) A company claims to produce a power generation device that produces 7 kW of power, takes in 11 kW of heat at a temperature of 840 K and rejects 8 kW of heat at 280 K.
We evaluate this claim: The work and heat flows are as in Fig. 5.2. Evaluation of the first law shows that Q˙ H = Q˙ L + W˙ should hold. With
A Heat Engine
An engine that operates at steady state between two reservoirs at TH = 750 ◦C and TL = 15 ◦C, has a heat intake of 0.1 MW, and rejects 50 kW of heat to the low temperature environment. We compute the power produced, the thermal efficiency, the entropy generation rate, and the work loss to irreversibilities.
Refrigerator
A restaurant refrigerator located in a kitchen at 21 ◦C maintains its int rior at 4 ◦C. The refrigerator consumes 300 W of power with a coefficient of performance COPR = 3. We compute entropy generation and work loss.
The work loss to irreversibilities is W˙ loss = TH S˙gen = 247.7 W; this work is required as input to overcome irreversibilities. A fully reversible refrigerator, i.e., a Carnot refrigerator, which removes the same amount of heat Q˙ L has a COPR,C = 1/ / TH − 1 = 16.3, and would consume 55 W of electrical power.
Note that efficient operation of a refrigerator is not only achieved by in- creasing its COP, but also by improving the thermal insulation. Indeed, the heat Q˙ L that is removed from the interior has crept in through the insulated walls of the refrigerator. Better insulation reduces the amount of heat that must be removed, and thus the work consumption of the refrigerator.
Heat Pump with Internal and External Irreversibilities
A heat pump is used to keep a home at 20 ◦C. The heat pump draws heat from the outside environment at 0 ◦C; its heating power is Q˙ H = 2 kW for a power consumption of W˙ = 0.5 kW. In order to facilitate sufficient heat transfer, a temperature difference of 10 K is required between the working substance of the heat pump and the respective environments. Figure 5.8 gives a sketch of the heat and work flows, and the relevant temperature levels.
We evaluate the process step by step. Let us first consider a perfectly reversible Carnot heat pump, that is a device that can operate at the actual temperatures of the two environments, TH = 293 K and TL = 273 K. The coefficient of performance of such an ideal engine is