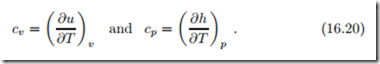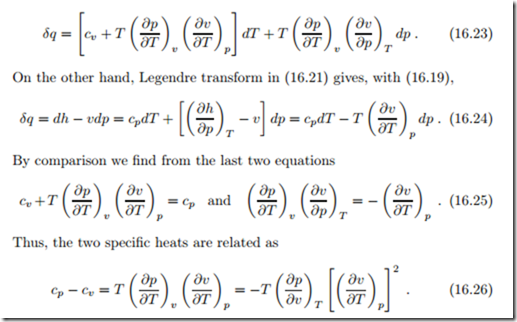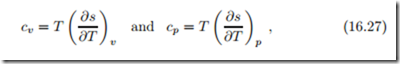Relation between Specific Heats
Our first use of (16.17) is to derive a relation between the specific heats at constant volume and constant pressure,
It will be seen that, as long as the thermal equation of state is known, it suffices to measure one of the specific heats, the other can then be determined from the relation to be derived.
We start with the first law for reversible processes in differential form, du = δq − pdv, and insert u (T, v), so that with the above definition of cv
For a constant volume process we have dv = 0 and thus δq = cv dT which relates the specific heat cv to the heat that must be added in an isochoric process to raise the temperature by dT ; in fact this is the definition of cv as a measurable quantity. Measurement of the specific heat cv (T, v) is done in calorimeters, where a substance in a rigid container (dv = 0) originally at temperature T is carefully heated by a known amount δq, e.g., by means of a electrical resistor, and the corresponding temperature change dT is recorded. Great care must be taken to control heat leaks, so that the amount of heat added to the material is known as accurately as possible.
To introduce the specific heat at constant pressure, cp, we proceed as follows: In the last equation, we consider volume v as function of T and p by means of the thermal equation of state v (T, p), so that to obtain
The right hand side is known when the thermal equation of state, p (T, v), is known. Thus, if one of the specific heats and the thermal equation of state are measured, the other specific heat is known. It is easy to show from the above that for the ideal gas cp − cv = R.
Finally, we note that straightforward application of the Gibbs equation in (16.20) yields the equivalent expressions for the specific heats
see the above derivation of (16.16) for details.