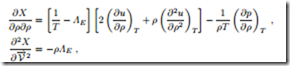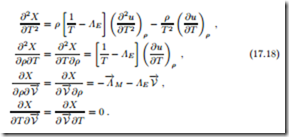Thermodynamic Stability
The equilibrium state determined in the previous sections should be stable, which means that, indeed, it should be a maximum of the integral Φ as defined in (17.4). This requires that the second variation of Φ must be negative. In our case, where the integrand X depends only on y, this requires negative values for the second derivatives ∂2X/∂y2 at the location of the maximum. With the help of the Gibbs equation, the second derivatives can be written as
These must now be evaluated at the equilibrium state, T = 1/ΛE and where they must be negative. With the definitions of isothermal compressibility κT (16.37) and the specific heat at constant volume cv (16.20), the resulting conditions can be written as
all mixed derivatives vanish in equilibrium. With the mass density being positive, thermodynamic stability thus requires that isothermal compressibility, specific heat, and thermodynamic temperature are positive,
These conditions imply that the volume decreases when pressure is increased isothermally, and that the temperature rises when heat is added to the sys- tem. While this matches our daily experience, it is nevertheless remarkable that it is guaranteed by the second law as a universal principle, valid for all materials.