THE MAGNETIZATION INDUCTANCE

Let us consider first a sinusoidal airgap flux density in the airgap, at no load (zero rotor currents). Making use of Ampere’s law we get, for airgap flux amplitude,

Bg1 ≈ 0gK K1c phases ; Ks >1 where F1 is the phase mmf/pole amplitude,

(5.114)

( )F1 phase = 2W I1 0 πp21K Kq1 y1

For a three-phase machine on no load, (5.115)

µ ( )F

F1m = 3WI1 0 π2p1K Kq1 y1 (5.116)

Now the flux per pole, for the fundamental Φ1, is

Φ =1 Bg1τLe (5.117)

So the airgap flux linkage per phase (a = 1) Ψ11h is

ψ11h = W K1 q1K y1Φ1 (5.118)

The magnetization inductance of a phase, when all other phases on stator and rotor are open, L_11m is

= 11h = 0 (WK K1 q1 y1)2 Leτ ψ 4µ

L11m I 2 π2 p gK K1 c s (5.119)

0

K_s–total saturation factor.

In a similar manner, for a harmonic ν, we obtain

L11mν = 4µ0 (WK K1π2qν yν)2 p gK K1 Lecτ sν ; Ksν ≈ (1 1.2− ) (5.120)

The saturation coefficient K_sν tends to be smaller than K_s, as the length of harmonics flux line in iron is usually shorter than for the fundamental. Now, for three-phase supply we use the same rationale, but, in the (5.114) F_1m will replace (F₁)_phase.

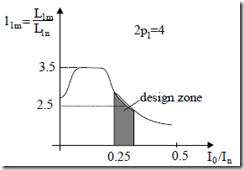
L1mν = 6µ0 (W K Kπ ν12 q2ν yν)2 p gK K1 Lecτ sν (5.121) When the no-load current (I_o/I_n) increases, the saturation factor increases, so the magnetization inductance L_1m decreases (Figure 5.25).

L1m = 0 1π2q1 y1 p gK K I /I1 cLes ( 0 n )

In general, a normal inductance, Ln, is defined as (5.122)

V_n, I_n, ω_1n rated phase voltage, current, and frequency of the respective machine. Well designed induction motors have l_1m (Figure 5.25) in the interval 2.5 to 4; in general, it increases with power level and decreases with large number of polesLn = Vωn :l1m = L1m (5.123)

Figure 5.25 Magnetization inductance versus no load current I₀/I_n

It should be noticed that Figure 5.25 shows yet another way (scale) of representing the magnetization curve.

The magnetization inductance of the rotor L_22m has expressions similar to (5.119) – (5.120), but with corresponding number of turns phase, distribution, and chording factors.

However, for the mutual magnetising inductance between a stator and rotor phase L_12m, we obtain

L12mν = 4πµ20 (W K1 qνsKyνsW K2 qνrKyνrKcνr )p gK1Leτsν (5.124)

This time, the skewing factor is present (skewed rotor slots). From (5.124) and (5.120),

LL1211mmνν = W K2W KqνrK_νsyKνryKνscνr (5.125)

1 q

It is now evident that for a rotor cage, K_qν^r = K_yν^r = 1 as each bar (slot) may be considered as a separate phase with W₂ = ½ turns.

The inductance L_11m or L_22m are also called main (magnetization) self inductances, while L_1m is called the cyclic (multiphase supply) magnetizing inductance. In general, for m phases,

L_1m ^{= m}2 L_11m ; m = 3 for three phases (5.126)

Example 5.1. The magnetization inductance L_1m calculation

For the motor M1 geometry given in the previous paragraph, with doublelayer winding and N_s = 36 slots, N_r = 30 slots, 2p₁ = 4, y/τ = 8/9, let us calculate L_1m and no-load phase current I₀ for a saturation factor K_s = 2.6 and B_g1 = 0.9T, K_st = K_sr = 1.8, K_c = 1.3 (Figure 5.20, 5.21).

Stator (rotor) slot opening are: b_os = 6g, b_or = 3g, W₁ = 120turns/phase, L_e = 0.12m, and stator bore diameter D_i/2= 0.051m.

Solution

• The Carter coefficient Kc ((5.4), (5.3)) is

= τ^{s,r = }1.²⁸⁰ (5.127) Kc1,2 τ_s,r − γ_1,2 ⋅g / 2 1.0837 τ =^s π^ND^s1 = π⋅ ⋅2 0.³⁶ 051 ₌ 9.59 10⋅ −3m (5.128)

τ =_r m

γ1 = 5(2+2bb2osb/ gos/ g/ g))22 = 512+62122 ==3.8.2747 (5.129)

γ 2 = 5+ 2orbor / g = 5+ 6

K_c = K_c1 ⋅K_c2 =1.280⋅1.0837 =1.327 (5.130)

• The distribution and chording factors Kq1, Ky1, (5.100), (5.103) are

K_q1  

From (5.122),

(5.132)

H

• The no load current I₀ from (5.114) is

⋅ ⁻³ ⋅ ⋅ ⋅ ⋅ ⋅

L 6

So the no load phase current I0 is

I0 = 3.12A

Let us consider rated current In = 2.5I0.

• The emf per phase for f1 = 60Hz is

(5.134)

E1 = 2πf L1 1mI0 = 2π60⋅0.1711⋅3.12 = 201.17V

With a rated voltage/phase V1 = 210 V, the relative value of L1m is

(5.135)

L

(5.136)

V /1 1In 210/ 2 60 2.5 3.12

It is obviously a small relative value, mainly due to the large value of saturation factor Ks = 2.6 (in the absence of saturation: Ks = 1.0).

In general, E1/V1 ≈ 0.9 – 0.98; higher values correspond to larger power machines.

Incoming search terms:

• rexuiz