Chapter 9: Alternative Architectures
9.1 Introduction
Quality is never an accident; it is always the result of high intention, sincere effort, intelligent direction and skillful execution; it represents the wise choice of many alternatives.
—William A. Foster
It would appear that we have reached the limits of what it is possible to achieve with computer technology, although one should be careful with such statements, as they tend to sound pretty silly in 5 years.
—John von Neumann, 1949
Our previous chapters have featured excursions into the background of computing technology. The presentations have been distinctly focused on uniprocessor systems from a computer science practitioner’s point of view. We hope that you have gained an understanding of the functions of various hardware components and can see how each contributes to overall system performance. This understanding is vital not only to hardware design, but also to efficient algorithm implementation. Most people gain familiarity with computer hardware through their experiences with personal computers and workstations. This leaves one significant area of computer architecture untouched: that of alternative architectures. Therefore, the focus of this chapter is to introduce you to a few of the architectures that transcend the classical von Neumann approach.
This chapter discusses RISC machines, architectures that exploit instruction-level parallelism, and multiprocessing architectures (with a brief introduction to parallel processing). We begin with the notorious RISC versus CISC debate to give you an idea of the differences between these two ISAs and their relative advantages and disadvantages. We then provide a taxonomy by which the various architectures may be classified, with a view as to how the parallel architectures fit into the classification. Next, we consider topics relevant to instruction-level parallel architectures, emphasizing superscalar architectures and reintroducing EPIC (explicitly parallel instruction computers) and VLIW (very long instruction word) designs. Finally, we provide a brief introduction to multiprocessor systems and some alternative approaches to parallelism.
Computer hardware designers began to reevaluate various architectural principles in the early 1980s. The first target of this reevaluation was the instruction set architecture. The designers wondered why a machine needed an extensive set of complex instructions when only about 20% of the instructions were used most of the time. This question led to the development of RISC machines, which we first introduced in Chapters 4 and 5, and to which we now devote an entire section of this chapter. The pervasiveness of RISC designs has led to a unique marriage of CISC with RISC. Many architectures now employ RISC cores to implement CISC architectures.
Chapters 4 and 5 described how new architectures, such as VLIW, EPIC, and multiprocessors, are taking over a large percentage of the hardware market. The invention of architectures exploiting instruction-level parallelism has led to techniques that accurately predict the outcome of branches in program code before the code is executed. Prefetching instructions based on these predictions has greatly increased computer performance. In addition to predicting the next instruction to fetch, high degrees of instruction-level parallelism have given rise to ideas such as speculative execution, where the processor guesses the value of a result before it has actually been calculated.
The subject of alternative architectures also includes multiprocessor systems. For these architectures, we return to the lesson we learned from our ancestors and the friendly ox. If we are using an ox to pull out a tree, and the tree is too large, we don’t try to grow a bigger ox. Instead, we use two oxen. Multiprocessing architectures are analogous to the oxen. We need them if we are to budge the stumps of intractable problems. However, multiprocessor systems present us with unique challenges, particularly with respect to cache coherence and memory consistency.
We note that although some of these alternative architectures are taking hold, their real advancement is dependent upon their incremental cost. Currently, the relationship between the performance delivered by advanced systems and their cost is nonlinear, with the cost far exceeding performance gains in most situations. This makes it cost prohibitive to integrate these architectures into mainstream applications. Alternative architectures do have their place in the market, however. Highly numerical science and engineering applications demand machines that outperform standard uniprocessor systems. For computers in this league, cost is usually not an issue.
As you read this chapter, keep in mind the previous computer generations introduced in Chapter 1. Many people believe that we have entered a new generation based on these alternative architectures, particularly in the area of parallel processing.
9.2 RISC Machines
We introduced RISC architectures in the context of instruction set design in Chapters 4 and 5. Recall that RISC machines are so named because they originally offered a smaller instruction set as compared to CISC machines. As RISC machines were being developed, the term “reduced” became somewhat of a misnomer, and is even more so now. The original idea was to provide a set of minimal instructions that could carry out all essential operations: data movement, ALU operations, and branching. Only explicit load and store instructions were permitted access to memory.
Complex instruction set designs were motivated by the high cost of memory. Having more complexity packed into each instruction meant that programs could be smaller, thus occupying less storage. CISC ISAs employ variable-length instructions, which keeps the simple instructions short, while also allowing for longer, more complicated instructions. Additionally, CISC architectures include a large number of instructions that directly access memory. So what we have at this point is a dense, powerful, variable-length set of instructions, which results in a varying number of clock cycles per instruction. Some complex instructions, particularly those instructions that access memory, require hundreds of cycles. In certain circumstances, computer designers have found it necessary to slow down the system clock (making the interval between clock ticks larger) to allow sufficient time for instructions to complete. This all adds up to longer execution time.
Human languages exhibit some of the qualities of RISC and CISC and serve as a good analogy to understand the differences between the two. Suppose you have a Chinese pen pal. Let’s assume each of you speak and write fluently in both English and Chinese. You both wish to keep the cost of your correspondence at a minimum, although you both enjoy sharing long letters. You have a choice between using expensive airmail paper, which will save considerable postage, or using plain paper and paying extra for stamps. A third alternative is to pack more information onto each written page.
As compared to the Chinese language, English is simple but verbose. Chinese characters are more complex than English words, and what might require 200 English letters might require only 20 Chinese characters. Corresponding in Chinese requires fewer symbols, saving on both paper and postage. However, reading and writing Chinese requires more effort, because each symbol contains more information. The English words are analogous to RISC instructions, whereas the Chinese symbols are analogous to CISC instructions. For most English-speaking people, “processing” the letter in English would take less time, but would also require more physical resources.
Although many sources tout RISC as a new and revolutionary design, its seeds were sown in the mid-1970s through the work of IBM’s John Cocke. Cocke started building his experimental Model 801 mainframe in 1975. This system initially received little attention, its details being disclosed only many years later. In the interim, David Patterson and David Ditzel published their widely acclaimed “Case for a Reduced Instruction Set Computer” in 1980. This paper gave birth to a radically new way of thinking about computer architecture, and brought the acronyms CISC and RISC into the lexicon of computer science. The new architecture proposed by Patterson and Ditzel advocated simple instructions, all of the same length. Each instruction would perform less work, but the time required for instruction execution would be constant and predictable.
Support for RISC machines came by way of programming observations on CISC machines. These studies revealed that data movement instructions accounted for approximately 45% of all instructions, ALU operations (including arithmetic, comparison, and logical) accounted for 25%, and branching (or flow control) amounted to 30%. Although many complex instructions existed, few were used. This finding, coupled with the advent of cheaper and more plentiful memory, and the development of VLSI technology, led to a different type of architecture. Cheaper memory meant that programs could use more storage. Larger programs consisting of simple, predictable instructions could replace shorter programs consisting of complicated and variable length instructions. Simple instructions would allow the use of shorter clock cycles. In addition, having fewer instructions would mean fewer transistors were needed on the chip. Fewer transistors translated to cheaper manufacturing costs and more chip real estate available for other uses. Instruction predictability coupled with VLSI advances would allow various performance-enhancing tricks, such as pipelining, to be implemented in hardware. CISC does not provide this diverse array of performance-enhancement opportunities.
We can quantify the differences between RISC and CISC using the basic computer performance equation as follows:
Computer performance, as measured by program execution time, is directly proportional to clock cycle time, the number of clock cycles per instruction, and the number of instructions in the program. Shortening the clock cycle, when possible, results in improved performance for RISC as well as CISC. Otherwise, CISC machines increase performance by reducing the number of instructions per program. RISC computers minimize the number of cycles per instruction. Yet both architectures can produce identical results in approximately the same amount of time. At the gate level, both systems perform an equivalent quantity of work. So what’s going on between the program level and the gate level?
CISC machines rely on microcode to tackle instruction complexity. Microcode tells the processor how to execute each instruction. For performance reasons, microcode is compact, efficient, and it certainly must be correct. Microcode efficiency, however, is limited by variable length instructions, which slow the decoding process, and a varying number of clock cycles per instruction, which makes it difficult to implement instruction pipelines. Moreover, microcode interprets each instruction as it is fetched from memory. This additional translation process takes time. The more complex the instruction set, the more time it takes to look up the instruction and engage the hardware suitable for its execution.
RISC architectures take a different approach. Most RISC instructions execute in one clock cycle. To accomplish this speedup, microprogrammed control is replaced by hardwired control, which is faster at executing instructions. This makes it easier to do instruction pipelining, but more difficult to deal with complexity at the hardware level. In RISC systems, the complexity removed from the instruction set is pushed up a level into the domain of the compiler.
To illustrate, let’s look at an instruction. Suppose we want to compute the product, 5 x 10. The code on a CISC machine might look like this:
mov ax, 10 mov bx, 5 mul bx, ax
A minimalistic RISC ISA has no multiplication instructions. Thus, on a RISC system our multiplication problem would look like this:
mov ax, 0
mov bx, 10
mov cx, 5
Begin: add ax, bx
loop Begin ;causes a loop cx times
The CISC code, although shorter, requires more clock cycles to execute. Suppose that on each architecture, register-to-register moves, addition, and loop operations each consume one clock cycle. Suppose also that a multiplication operation requires 30 clock cycles. Comparing the two code fragments we have:[1]
CISC instructions:
Total clock cycles = (2 movs x 1 clock cycle) + (1 mul x 30 clock cycles)
= 32 clock cycles
RISC instructions:
Total clock cycles = (3 movs x 1 clock cycle) + (5 adds x 1 clock cycle)
+ (5 loops x 1 clock cycle)
= 13 clock cycles
Add to this the fact that RISC clock cycles are often shorter than CISC clock cycles, and it should be clear that even though there are more instructions, the actual execution time is less for RISC than for CISC. This is the main inspiration behind the RISC design.
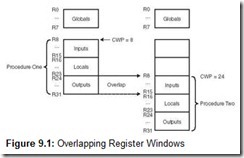
We have mentioned that reducing instruction complexity results in simpler chips. Transistors formerly employed in the execution of CISC instructions are used for pipelines, cache, and registers. Of these three, registers offer the greatest potential for improved performance, so it makes sense to increase the number of registers and to use them in innovative ways. One such innovation is the use of register window sets. Although not as widely accepted as other innovations associated with RISC architectures, register windowing is nevertheless an interesting idea and is briefly introduced here.
High-level languages depend on modularization for efficiency. Procedure calls and parameter passing are natural side effects of using these modules. Calling a procedure is not a trivial task. It involves saving a return address, preserving register values, passing parameters (either by pushing them on a stack or using registers), branching to the subroutine, and executing the subroutine. Upon subroutine completion, parameter value modifications must be saved, and previous register values must be restored before returning execution to the calling program. Saving registers, passing parameters, and restoring registers involves considerable effort and resources. With RISC chips having the capacity for hundreds of registers, the saving and restoring sequence can be reduced to simply changing register environments.
To fully understand this concept, try to envision all registers as being divided into sets. When a program is executing in one environment, only one certain register set is visible. If the program changes to a different environment (say a procedure is called), the visible set of registers for the new environment changes. For example, while the main program is running, perhaps it sees only registers 0 through 9. When a certain procedure is called, perhaps it will see registers 10 through 19. Typical values for real RISC architectures include 16 register sets (or windows) of 32 registers each. The CPU is restricted to operating in only one single window at any given time. Therefore, from the programmer’s perspective, there are only 32 registers available.
Register windows, by themselves, do not necessarily help with procedure calls or parameter passing. However, if these windows are overlapped carefully, the act of passing parameters from one module to another becomes a simple matter of shifting from one register set to another, allowing the two sets to overlap in exactly those registers that must be shared to perform the parameter passing. This is accomplished by dividing the register window set into distinct partitions, including global registers (common to all windows), local registers (local to the current window), input registers (which overlap with the preceding window’s output registers), and output registers (which overlap with the next window’s input registers). When the CPU switches from one procedure to the next, it switches to a different register window, but the overlapping windows allow parameters to be “passed” simply by changing from output registers in the calling module to input registers in the called module. A current window pointer (CWP) points to the register window set to be used at any given time.
Consider a scenario in which Procedure One is calling Procedure Two. Of the 32 registers in each set, assume 8 are global, 8 are local, 8 are for input, and 8 are for output. When Procedure One calls Procedure Two, any parameters that need to be passed are put into the output register set of Procedure One. Once Procedure Two begins execution, these registers become the input register set for Procedure Two. This process is illustrated in Figure 9.1.
One more important piece of information to note regarding register windows on RISC machines is the circular nature of the set of registers. For programs having a high degree of nesting, it is possible to exhaust the supply of registers. When this happens, main memory takes over, storing the lowest numbered windows, which contain values from the oldest procedure activations. The highest numbered register locations (the most recent activations) then wrap around to the lowest numbered registers. As returns from procedures are executed, the level of nesting decreases, and register values from memory are restored in the order in which they were saved.
In addition to simple, fixed-length instructions, efficient pipelines in RISC machines have provided these architectures with an enormous increase in speed. Simpler instructions have freed up chip real estate, resulting in not only more usable space, but also in chips that are easier and less time consuming to design and manufacture.
You should be aware that it is becoming increasingly difficult to categorize today’s processors as either RISC or CISC. The lines separating these architectures have blurred. Some current architectures use both approaches. If you browse some of the newer chip manuals, you will see that today’s RISC machines have more extravagant and more complex instructions than some CISC machines. The RISC PowerPC, for example, has a larger instruction set than the CISC Pentium. As VLSI technology continues to make transistors smaller and cheaper, the expansiveness of the instruction set is now becoming less of an issue in the CISC versus RISC debate, whereas register usage and the load/store architecture is becoming more prominent.
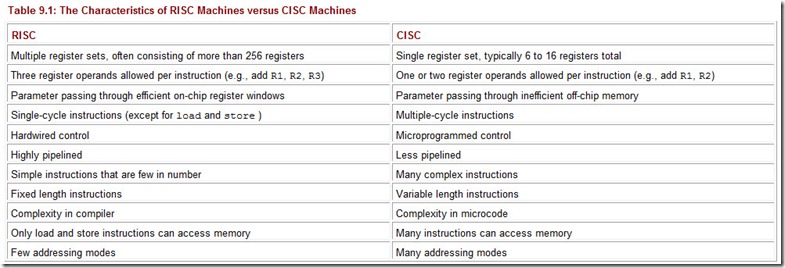
With that being said, we cautiously provide Table 9.1 as a summary of the classical differences between RISC and CISC.
As we have mentioned, although many sources praise the revolutionary innovations of RISC design, many of the ideas used in RISC machines (including pipelining and simple instructions) were implemented on mainframes in the 1960s and 1970s. There are many so-called new designs that aren’t really new, but are simply recycled. Innovation does not necessarily mean inventing a new wheel; it may be a simple case of figuring out the best way to use a wheel that already exists. This is a lesson that will serve you well in your career in the computing field.
[1] This is not an unrealistic number-a multiplication on an Intel 8088 requires 133 clock cycles for two 16-bit numbers.
9.3 Flynn’s Taxonomy
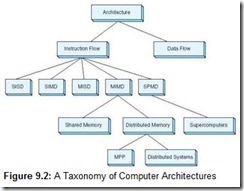
Over the years, several attempts have been made to find a satisfactory way to categorize computer architectures. Although none of them are perfect, today’s most widely accepted taxonomy is the one proposed by Michael Flynn in 1972. Flynn’s taxonomy considers two factors: the number of instructions and the number of data streams that flow into the processor. A machine can have either one or multiple streams of data, and can have either one or multiple processors working on this data. This gives us four possible combinations: SISD (single instruction stream, single data stream), SIMD (single instruction stream, multiple data streams), MISD (multiple instruction streams, single data stream), and MIMD (multiple instruction streams, multiple data streams).
Uniprocessors are SISD machines. SIMD machines, which have a single point of control, execute the same instruction simultaneously on multiple data values. The SIMD category includes array processors, vector processors, and systolic arrays. MISD machines have multiple instruction streams operating on the same data stream. MIMD machines, which employ multiple control points, have independent instruction and data streams. Multiprocessors and most current parallel systems are MIMD machines. SIMD computers are simpler to design than MIMD machines, but they are also considerably less flexible. All of the SIMD multiprocessors must execute the same instruction simultaneously. If you think about this, executing something as simple as conditional branching could quickly become very expensive.
Flynn’s taxonomy falls short in several areas. For one, there seem to be very few (if any) applications for MISD machines. Secondly, Flynn assumed that parallelism was homogeneous. A collection of processors can be homogeneous or heterogeneous. A machine could conceivably have four separate floating-point adders, two multipliers, and a single integer unit. This machine could therefore execute seven operations in parallel, but it does not readily fit into Flynn’s classification system.
Another problem with this taxonomy is with the MIMD category. An architecture with multiple processors falls into this category without consideration for how the processors are connected or how they view memory. There have been several attempts to refine the MIMD category. Suggested changes include subdividing MIMD to differentiate systems that share memory from those that don’t, as well as categorizing processors according to whether they are bus-based or switched.
Shared memory systems are those in which all processors have access to a global memory and communicate through shared variables, just as processes do on a uniprocessor. If multiple processors do not share memory, each processor must own a portion of memory. Consequently, all processors must communicate by way of message passing, which can be expensive and inefficient. The issue some people have with using memory as a determining factor for classifying hardware is that shared memory and message passing are actually programming models, not hardware models. Thus, they more properly belong in the domain of system software.
The two major parallel architectural paradigms, SMP (symmetric multiprocessors) and MPP (massively parallel processors), are both MIMD architectures, but differ in how they use memory. SMP machines, such as a dual-processor Intel PC and the 256-processor Origin3000, share memory, whereas MPP processors, such as the nCube, CM5, and Cray T3E, do not. These particular MPP machines typically house thousands of CPUs in a single large cabinet connected to hundreds of gigabytes of memory. The price of these systems can run into millions of dollars.
Originally, the term MPP described tightly coupled SIMD multiprocessors, such as the Connection Machine and Goodyear’s MPP. Today, however, the term MPP is used to refer to parallel architectures that have multiple self-contained nodes with private memories, all of which have the ability to communicate via a network. An easy way to differentiate SMP and MPP (by today’s definition) is the following:
MPP = many processors + distributed memory + communication via network
and
SMP = few processors + shared memory + communication via memory
Distributed computing is another example of the MIMD architecture. Distributed computing is typically defined as a set of networked computers that work collaboratively to solve a problem. This collaboration, however, can occur in many different ways.
A network of workstations (NOW) is a collection of distributed workstations that works in parallel only while the nodes are not being used as regular workstations. NOWs typically consist of heterogeneous systems, with different processors and software, that communicate via the Internet. Individual users must establish the appropriate connection to the network before joining the parallel computation. A cluster of workstations (COW ) is a collection similar to a NOW, but it requires that a single entity be in charge. Nodes typically have common software, and a user that can access one node can usually access all nodes. A dedicated cluster parallel computer (DCPC) is a collection of workstations specifically collected to work on a given parallel computation. The workstations have common software and file systems, are managed by a single entity, communicate via the Internet, and aren’t used as workstations. A pile of PCs (POPC) is a cluster of dedicated heterogeneous hardware used to build a parallel system. Whereas a DCPC has relatively few, but expensive and fast components, a POPC uses a large number of slow, but relatively cheap nodes.
The BEOWULF project, introduced in 1994 by Thomas Sterling and Donald Becker of Goddard Space Flight Center, is a POPC architecture that has successfully bundled various hardware platforms with specially designed software, resulting in an architecture that has the look and feel of a unified parallel machine. The nodes on a BEOWULF network are always connected via a private network. If you have an old Sun SPARC, a couple of 486 machines, a DEC Alpha (or simply a large collection of dusty Intel machines!), and a means to connect them into a network, you can install the BEOWULF software and create your own personal, but extremely powerful, parallel computer.
Flynn’s taxonomy has recently been expanded to include SPMD (single program multiple data) architectures. An SPMD consists of multiprocessors, each with its own data set and program memory. The same program is executed on each processor, with synchronization at various global control points. Although each processor loads the same program, each may execute different instructions. For example, a program may have code that resembles:
If myNodeNum = 1 do this, else do that
In this way, different nodes execute different instructions within the same program. SPMD is actually a programming paradigm used on MIMD machines and differs from SIMD in that the processors can do different things at the same time. Supercomputers often use an SPMD design.
At a level above where Flynn begins his taxonomy, we need to add one more characteristic, and that is whether the architecture is instruction driven or data driven. The classic von Neumann architecture is instruction driven. All processor activities are determined by a sequence of program code. Program instructions act on the data. Data driven, or dataflow, architectures do just the opposite. The characteristics of the data determine the sequence of processor events. We explore this idea in more detail in Section 9.5.
With the addition of dataflow computers and some refinements to the MIMD classification, we obtain the taxonomy shown in Figure 9.2. You may wish to refer to it as you read the sections that follow. We begin on the left-hand branch of the tree, with topics relevant to SIMD and MIMD architectures.
9.4 Parallel and Multiprocessor Architectures
Since the beginning of computing, scientists have endeavored to make machines solve problems better and faster. Miniaturization technology has resulted in improved circuitry, and more of it on a chip. Clocks have become faster, leading to CPUs in the gigahertz range. However, we know that there are physical barriers that control the extent to which single-processor performance can be improved. Heat and electromagnetic interference limit chip transistor density. Even if (when?) these problems are solved, processor speeds will always be constrained by the speed of light. On top of these physical limitations, there are also economic limitations. At some point, the cost of making a processor incrementally faster will exceed the price that anyone is willing to pay. Ultimately, we will be left with no feasible way of improving processor performance except to distribute the computational load among several processors. For these reasons, parallelism is becoming increasingly popular.
It is important to note, however, that not all applications can benefit from parallelism. For example, multiprocessing parallelism adds cost (such as process synchronization and other aspects of process administration). If an application isn’t amenable to a parallel solution, generally it is not cost effective to port it to a multiprocessing parallel architecture.
Implemented correctly, parallelism results in higher throughput, better fault tolerance, and a more attractive price/performance ratio. Although parallelism can result in significant speedup, this speedup can never be perfect. Given n processors running in parallel, perfect speedup would imply that a computational job could complete in ![]() time, leading to an n-fold increase in power (or a runtime decrease by a factor of n).
time, leading to an n-fold increase in power (or a runtime decrease by a factor of n).
We need only recall Amdahl’s Law to realize why perfect speedup is not possible. If two processing components run at two different speeds, the slower speed will dominate. This law also governs the speedup attainable using parallel processors on a problem. No matter how well you parallelize an application, there will always be a small portion of work done by one processor that must be done serially. Additional processors can do nothing but wait until the serial processing is complete. The underlying premise is that every algorithm has a sequential part that ultimately limits the speedup achievable through a multiprocessor implementation. The greater the sequential processing, the less cost effective it is to employ a multiprocessing parallel architecture.
Using multiple processors on a single task is only one of many different types of parallelism. In earlier chapters, we introduced a few of these including pipelining, VLIW, and ILP, giving motivations for each particular type. Other parallel architectures deal with multiple (or parallel) data. Examples include SIMD machines such as vector, neural, and systolic processors. There are many architectures that allow for multiple or parallel processes, characteristic of all MIMD machines. It is important to note that “parallel” can have many different meanings, and it is equally important to be able to differentiate among them.
We begin this section with a discussion of examples of ILP architectures, and then move on to SIMD and MIMD architectures. The last section introduces alternative (less mainstream) parallel processing approaches, including systolic arrays, neural networks, and dataflow computing.
9.4.1 Superscalar and VLIW
In this section we revisit the concept of superscalar architectures and compare them to VLIW architectures. Superscalar and VLIW architectures both exhibit instruction-level parallelism, but differ in their approach. To set the stage for our discussion, we start with a definition of superpipelining. Recall that pipelining divides the fetch-decode-execute cycle into stages, in which a set of instructions is in different stages at the same time. In a perfect world, one instruction would exit the pipe every clock cycle. However, because of branching instructions and data dependencies in the code, the goal of one instruction per cycle is never quite achieved.
Superpipelining occurs when a pipeline has stages that require less than half a clock cycle to execute. An internal clock can be added which, when running at double the speed of the external clock, can complete two tasks per external clock cycle. Although superpipelining is equally applicable to both RISC and CISC architectures, it is most often incorporated in RISC processors. Superpipelining is one aspect of superscalar design, and for this reason, there is often confusion regarding which is which.
So, what exactly is a superscalar processor? We know that the Pentium processor is superscalar, but have yet to discuss what this really means. Superscalar is a design methodology that allows multiple instructions to be executed simultaneously in each cycle. Although superscalar differs from pipelining in several ways that will be discussed shortly, the net effect is the same. The way in which superscalar designs achieve speedup is similar to the idea of adding another lane to a busy single lane highway. Additional “hardware” is required, but in the end, more cars (instructions) can get from point A to point B in the same amount of time.
The superscalar components analogous to our additional highway lanes are called execution units. Execution units consist of floating-point adders and multipliers, integer adders and multipliers, and other specialized components. Although the units may also work independently, it is important that the architecture have a sufficient number of these specialized units to process several instructions in parallel. It is not uncommon for execution units to be duplicated; for example, a system could have a pair of identical floating-point units. Often, the execution units are pipelined, providing even better performance.
A critical component of this architecture is a specialized instruction fetch unit, which can retrieve multiple instructions simultaneously from memory. This unit, in turn, passes the instructions to a complex decoding unit that determines whether the instructions are independent (and can thus be executed simultaneously) or whether a dependency of some sort exists (in which case not all instructions can be executed at the same time).
As an example, consider the IBM RS/6000. This processor had an instruction fetch unit and two processors, each containing a 6-stage floating-point unit and a 4-stage integer unit. The instruction fetch unit was set up with a 2-stage pipeline, where the first stage fetched packets of four instructions each, and the second stage delivered the instructions to the appropriate processing unit.
Superscalar computers are architectures that exhibit parallelism through pipelining and replication. Superscalar design includes superpipelining, simultaneous fetching of multiple instructions, a complex decoding unit capable of determining instruction dependencies and dynamically combining instructions to ensure no dependencies are violated, and sufficient quantities of resources for parallel execution of multiple instructions. We note that although this type of parallelism requires very specific hardware, a superscalar architecture also requires a sophisticated compiler to schedule operations that make the best use of machine resources.
Whereas superscalar processors rely on both the hardware (to arbitrate dependencies) and the compiler (to generate approximate schedules), VLIW processors rely entirely on the compiler. VLIW processors pack independent instructions into one long instruction, which, in turn, tells the execution units what to do. Many argue that because the compiler has a better overall picture of dependencies in the code, this approach results in better performance. However, the compiler cannot have an overall picture of the run-time code so it is compelled to be conservative in its scheduling.
As a VLIW compiler creates very long instructions, it also arbitrates all dependencies. The instructions, which are fixed at compile time, typically contain four to eight instructions. Because the instructions are fixed, any modification that could affect scheduling of instructions (such as changing memory latency) requires a recompilation of the code, potentially causing a multitude of problems for software vendors. VLIW supporters point out that this technology simplifies the hardware by moving complexity to the compiler. Superscalar supporters counter with the argument that VLIW can, in turn, lead to significant increases in the amount of code generated. For example, when program control fields are not used, memory space and bandwidth are wasted. In fact, a typical FORTRAN program explodes to double and sometimes triple its normal size when compiled on a VLIW machine.
Intel’s Itanium, IA-64, is one example of a VLIW processor. Recall that the IA-64 uses an EPIC style of VLIW processor. An EPIC architecture holds some advantages over an ordinary VLIW processor. Like VLIW, EPIC bundles its instructions for delivery to various execution units. However, unlike VLIW, these bundles need not be the same length. A special delimiter indicates where one bundle ends and another begins. Instruction words are prefetched by hardware, which identifies and then schedules the bundles in independent groups for parallel execution. This is an attempt to overcome the limitations introduced by the compiler’s lack of total knowledge of the run-time code. Instructions within bundles may be executed in parallel with no concern for dependencies, and thus no concern for ordering. By most people’s definition, EPIC is really VLIW. Although Intel might argue the point, and die-hard architects would cite the minor differences mentioned above (as well as a few others), EPIC is in reality an enhanced version of VLIW.
9.4.2 Vector Processors
Often referred to as supercomputers, vector processors are specialized, heavily pipelined processors that perform efficient operations on entire vectors and matrices at once. This class of processor is suited for applications that can benefit from a high degree of parallelism, such as weather forecasting, medical diagnoses, and image processing.
To understand vector processing, one must first understand vector arithmetic. A vector is a fixed-length, one-dimensional array of values, or an ordered series of scalar quantities. Various arithmetic operations are defined over vectors, including addition, subtraction, and multiplication.
Vector computers are highly pipelined so that arithmetic operations can be overlapped. Each instruction specifies a set of operations to be carried over an entire vector. For example, let’s say we want to add vectors V1 and V2 and place the results in V3. On a traditional processor our code would include the following loop:
for i = 0 to VectorLength V3[i] = V1[i] + V2[i];
However, on a vector processor, this code becomes
LDV V1, R1 ;load vector1 into vector register R1 LDV V2, R2 ADDV R3, R1, R2 STV R3, V3 ;store vector register R3 in vector V3
Vector registers are specialized registers that can hold several vector elements at one time. The register contents are sent one element at a time to a vector pipeline, and the output from the pipeline is sent back to the vector registers one element at a time. These registers are, therefore, FIFO queues capable of holding many values. Vector processors generally have several of these registers. The instruction set for a vector processor contains instructions for loading these registers, performing operations on the elements within the registers, and storing the vector data back to memory.
Vector processors are often divided into two categories according to how the instructions access their operands. Register-register vector processors require that all operations use registers as source and destination operands. Memory-memory vector processors allow operands from memory to be routed directly to the arithmetic unit. The results of the operation are then streamed back to memory. Register-to-register processors are at a disadvantage in that long vectors must be broken into fixed length segments that are small enough to fit into the registers. However, memory-to-memory machines have a large startup time due to memory latency. (Startup time is the time between initializing the instruction and the first result emerging from the pipeline.) After the pipeline is full, however, this disadvantage disappears.
Vector instructions are efficient for two reasons. First, the machine fetches significantly fewer instructions, which means there is less decoding, control unit overhead, and memory bandwidth usage. Second, the processor knows it will have a continuous source of data and can begin prefetching corresponding pairs of values. If interleaved memory is used, one pair can arrive per clock cycle. The most famous vector processors are the Cray series of supercomputers. Their basic architecture has changed little over the past 25 years.
9.4.3 Interconnection Networks
In parallel MIMD systems, communication is essential for synchronized processing and data sharing. The manner in which messages are passed among system components determines the overall system design. The two choices are to use shared memory or an interconnection network model. Shared memory systems have one large memory that is accessed identically by all processors. In interconnected systems, each processor has its own memory, but processors are allowed to access other processors’ memories via the network. Both, of course, have their strengths and weaknesses.
Interconnection networks are often categorized according to topology, routing strategy, and switching technique. The network topology, the way in which the components are interconnected, is a major determining factor in the overhead cost of message passing. Message passing efficiency is limited by:
-
Bandwidth—The information carrying capacity of the network.
-
Message latency—The time required for the first bit of a message to reach its destination.
-
Transport latency—The time the message spends in the network.
-
Overhead—Message processing activities in the sender and receiver.
Accordingly, network designs attempt to minimize both the number of messages required and the distances over which they must travel.
Interconnection networks can be either static or dynamic. Dynamic networks allow the path between two entities (either two processors or a processor and a memory) to change from one communication to the next, whereas static networks do not. Interconnection networks can also be blocking or nonblocking. Nonblocking networks allow new connections in the presence of other simultaneous connections, whereas blocking networks do not.
Static interconnection networks are used mainly for message passing and include a variety of types, many of which may be familiar to you. Processors are typically interconnected using static networks, whereas processor-memory pairs usually employ dynamic networks.
Completely connected networks are those in which all components are connected to all other components. These are very expensive to build, and as new entities are added, they become difficult to manage. Star-connected networks have a central hub through which all messages must pass. Although a hub can be a central bottleneck, it provides excellent connectivity. Linear array or ring networks allow any entity to directly communicate with its two neighbors, but any other communication has to go through multiple entities to arrive at its destination. (The ring is just a variation of a linear array in which the two end entities are directly connected.) A mesh network links each entity to four or six neighbors (depending on whether it is two-dimensional or three-dimensional). Extensions of this network include those that wrap around, similar to how a linear network can wrap around to form a ring.
Tree networks arrange entities in noncyclic structures, which have the potential for communication bottlenecks forming at the roots. Hypercube networks are multidimensional extensions of mesh networks in which each dimension has two processors. (Hypercubes typically connect processors, not processor-memory sets.) Two-dimensional hypercubes consist of pairs of processors that are connected by a direct link if, and only if, the binary representation of their labels differ in exactly one bit position. In an n-dimensional hypercube, each processor is directly connected to n other processors. It is interesting to note that the total number of bit positions at which two labels of a hypercube differ is called their Hamming distance, which is also the term used to indicate the number of communication links in the shortest path between two processors. Figure 9.3 illustrates the various types of static networks.
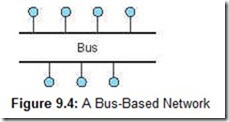
Dynamic networks allow for dynamic configuration of the network in one of two ways: either by using a bus or by using a switch that can alter the routes through the network. Bus-based networks, illustrated in Figure 9.4, are the simplest and most efficient when cost is a concern and the number of entities is moderate. Clearly, the main disadvantage is the bottleneck that can result from bus contention as the number of entities grows large. Parallel buses can alleviate this problem, but their cost is considerable.
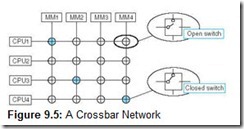
Switching networks use switches to dynamically alter routing. There are two types of switches: crossbar switches and 2 x 2 switches. Crossbar switches are simply switches that are either open or closed. Any entity can be connected to any other entity by closing the switch (making a connection) between them. Networks consisting of crossbar switches are fully connected because any entity can communicate directly with any other entity, and simultaneous communications between different processor/memory pairs are allowed. (A given processor can have at most one connection at a time, however.) No transfer is ever prevented due to a switch being closed. Therefore, the crossbar network is a nonblocking network. However, if there is a single switch at each crosspoint, n entities require n2 switches. In reality, many multiprocessors require many switches at each crosspoint. Thus, managing numerous switches quickly becomes difficult and costly. Crossbar switches are practical only in high-speed multiprocessor vector computers. A crossbar switch configuration is shown in Figure 9.5. The blue switches indicate closed switches. A processor can be connected to only one memory at a time, so there will be at most one closed switch per column.
The second type of switch is the 2 x 2 switch. It is similar to a crossbar switch, except that it is capable of routing its inputs to different destinations, whereas the crossbar simply opens or closes the communications channel. A 2 x 2 interchange switch has two inputs and two outputs. At any given moment, a 2 x 2 switch can be in one of four states: through, cross, upper broadcast, and lower broadcast, as shown in Figure 9.6. In the through state, the upper input is directed to the upper output and the lower input is directed to the lower output. More simply, the input is directed through the switch. In the cross state, the upper input is directed to the lower output, and the lower input is directed to the upper output. In upper broadcast, the upper input is broadcast to both the upper and lower outputs. In lower broadcast, the lower input is broadcast to both the upper and lower outputs. The through and cross states are the ones relevant to interconnection networks.
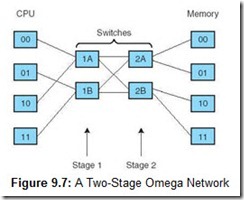
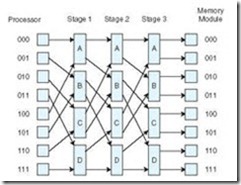
The most advanced class of networks, multistage interconnection networks, is built using 2 x 2 switches. The idea is to incorporate stages of switches, typically with processors on one side and memories on the other, with a series of switching elements as the interior nodes. These switches dynamically configure themselves to allow a path from any given processor to any given memory. The number of switches and the number of stages contribute to the path length of each communication channel. A slight delay may occur as the switch determines the configuration required to pass a message from the specified source to the desired destination. These multistage networks are often called shuffle networks, alluding to the pattern of the connections between the switches.
Many topologies have been suggested for multistage switching networks. These networks can be used to connect processors in loosely coupled distributed systems, or they can be used in tightly coupled systems to control processor-to-memory communications. A switch can be in only one state at a time, so it is clear that blocking can occur. For example, consider one simple topology for these networks, the Omega network shown in Figure 9.7. It is possible for CPU 00 to communicate with Memory Module 00 if both Switch 1A and Switch 2A are set to through. At the same time, however, it is impossible for CPU 10 to communicate with Memory Module 01. To do this, both Switch 1A and Switch 2A would need to be set to cross. This Omega network is, therefore, a blocking network. Nonblocking multistage networks can be built by adding more switches and more stages. In general, an Omega network of n nodes requires log2n stages with switches per stage.
It is interesting to note that configuring the switches is not really as difficult as it might seem. The binary representation of the destination module can be used to program the switches as the message travels the network. Using one bit of the destination address for each stage, each switch can be programmed based on the value of that bit. If the bit is a 0, the input is routed to the upper output. If the bit is a 1, the input is routed to the lower output. For example, suppose CPU 00 wishes to communicate with Memory Module 01. We can use the first bit of the destination (0) to set Switch 1A to through (which routes the input to the upper output), and the second bit (1) to set Switch 2A to cross (which routes the input to the lower output). If CPU 11 wishes to communicate with Memory Module 00, we would set Switch 1B to cross, and Switch 2A to cross (since both inputs must be routed to the upper outputs).
Another interesting method for determining the switch setting is to compare the corresponding bits of the source and destination. If the bits are equal, the switch is set to through. If the bits are different, the switch is set to cross. For example, suppose CPU 00 wishes to communicate with Memory Module 01. We compare the first bits of each (0 to 0), setting Switch 1A to through, and compare the second bits of each (0 to 1), setting Switch 2A to cross.
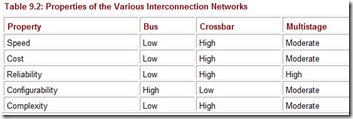
Each method for interconnecting multiprocessors has its advantages and disadvantages. For example, bus-based networks are the simplest and most efficient solution when a moderate number of processors is involved. However, the bus becomes a bottleneck if many processors make memory requests simultaneously. We compare bus-based, crossbar, and multistage interconnection networks in Table 9.2.
9.4.4 Shared Memory Multiprocessors
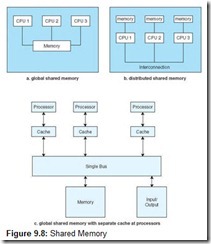
We have mentioned that multiprocessors are classified by how memory is organized. Tightly coupled systems use the same memory and are thus known as shared memory processors. This does not mean all processors must share one large memory. Each processor could have a local memory, but it must be shared with other processors. It is also possible that local caches could be used with a single global memory. These three ideas are illustrated in Figure 9.8.
The concept of shared memory multiprocessors (SMM) dates back to the 1970s. The first SMM machine was built at Carnegie-Mellon University using crossbar switches to connect 16 processors to 16 memory modules. The most widely acclaimed of the early SMM machines was the cm* system with its 16 PDP-11 processors and 16 memory banks, all of which were connected using a tree network. The global shared memory was divided equally among the processors. If a processor generated an address, it would first check its local memory. If the address was not found in local memory, it was passed on to a controller. The controller would try to locate the address within the processors that occupied the subtree for which it was the root. If the required address still could not be located, the request was passed up the tree until the data was found or the system ran out of places to look.
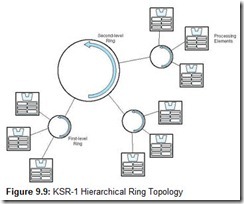
There are some commercial SMMs in existence, but they are not extremely popular. One of the first commercial SMM computers was the BBN (Bolt, Beranek, and Newman) Butterfly, which used 256 Motorola 68000 processors. The KSR-1 (from Kendall Square Research) has recently become available, and should prove quite useful for computational science applications. Each KSR-1 processor contains a cache, but the system has no primary memory. Data is accessed through cache directories maintained in each processor. The KSR-1 processing elements are connected in a unidirectional ring topology, as shown in Figure 9.9. Messages and data travel around the rings in only one direction. Each first-level ring can connect from 8 to 32 processors. A second level ring can connect up to 34 first-level rings, for a maximum of 1088 processors. When a processor references an item in, say, location x, the processor cache that contains address x places the requested cache slot on the ring. The cache entry (containing the data) migrates through the rings until it reaches the processor that made the request. Distributed shared memory systems of this type are called shared virtual memory systems.
Shared memory MIMD machines can be divided into two categories according to how they synchronize their memory operations. In Uniform Memory Access (UMA) systems, all memory accesses take the same amount of time. A UMA machine has one pool of shared memory that is connected to a group of processors through a bus or switch network. All processors have equal access to memory, according to the established protocol of the interconnection network. As the number of processors increases, a switched interconnection network (requiring 2n connections) quickly becomes very expensive in a UMA machine. Bus-based UMA systems saturate when the bandwidth of the bus becomes insufficient for the number of processors in the system. Multistage networks run into wiring constraints and significant latency if the number of processors becomes very large. Thus the scalability of UMA machines is limited by the properties of interconnection networks. Symmetric multiprocessors are well-known UMA architectures. Specific examples of UMA machines include Sun’s Ultra Enterprise, IBM’s iSeries and pSeries servers, the Hewlett-Packard 900, and DEC’s AlphaServer.
Nonuniform memory access (NUMA) machines get around the problems inherent in UMA architectures by providing each processor with its own piece of memory. The memory space of the machine is distributed across all of the processors, but the processors see this memory as a contiguous addressable entity. Although NUMA memory constitutes a single addressable entity, its distributed nature is not completely transparent. Nearby memory takes less time to read than memory that is further away. Thus, memory access time is inconsistent across the address space of the machine. An example of NUMA architectures include Sequent’s NUMA-Q and the Origin2000 by Silicon Graphics.
NUMA machines are prone to cache coherence problems. To reduce memory access time, each NUMA processor maintains a private cache. However, when a processor modifies a data element that is in its local cache, other copies of the data become inconsistent. For example, suppose Processor A and Processor B both have a copy of data element x in their cache memories. Let’s say x has a value of 10. If Processor A sets x to 20, Processor B’s cache (which still contains a value of 10) has an old, or stale, value of x. Inconsistencies in data such as this cannot be allowed, so mechanisms must be provided to ensure cache coherence. Specially designed hardware units known as snoopy cache controllers monitor all caches on the system. They implement the system’s cache consistency protocol. NUMA machines that employ snoopy caches and maintain cache consistency are referred to as CC-NUMA (cache coherent NUMA) architectures.
The easiest approach to cache consistency is to ask the processor having the stale value to either void x from its cache or to update x to the new value. When this is done immediately after the value of x is changed, we say that the system uses a write-through cache update protocol. With this approach, the data is written to cache and memory concurrently. If the write-through with update protocol is used, a message containing the new value of x is broadcast to all other cache controllers so that they can update their caches. If the write-through with invalidation protocol is used, the broadcast contains a message asking all cache controllers to remove the stale value of x from their caches. Write-invalidate uses the network only the first time x is updated, thus keeping bus traffic light. Write-update keeps all caches current, which reduces latency; however, it increases communications traffic.
A second approach to maintaining cache coherency is the use of a write-back protocol that changes only the data in cache at the time of modification. Main memory is not modified until the modified cache block must be replaced and thus written to memory. With this protocol, data values are read in the normal manner, but before data can be written, the processor performing the modification must obtain exclusive rights to the data. It does so by requesting ownership of the data. When ownership is granted, any copies of the data at other processors are invalidated. If other processors wish to read the data, they must request the value from the processor that owns it. The processor with ownership then relinquishes its rights and forwards the current data value to main memory.
9.4.5 Distributed Computing
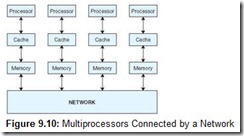
Distributed computing is another form of multiprocessing. Although it has become an increasingly popular source of computational power, it means different things to different people. In a sense, all multiprocessor systems are also distributed systems because the processing load is divided among a group of processors that work collectively to solve a problem. When most people use the term distributed system, they are referring to a very loosely coupled multicomputer system. Recall that multiprocessors can be connected using local buses (as in Figure 9.8c), or they can be connected through a network, as indicated in Figure 9.10. Loosely coupled distributed computers depend on a network for communication among processors.
This idea is exemplified by the recent practice of using individual microcomputers and NOWs for distributed computing systems. These systems allow idle PC processors to work on small pieces of large problems. A recent cryptographic problem was solved through the resources of thousands of personal computers, each performing brute-force cryptanalysis using a small set of possible message keys.
The University of California at Berkeley hosts a radio astronomy group, SETI (Search for Extra Terrestrial Intelligence), that analyzes data from radiotelescopes. To help with this project, PC users can install a SETI screen saver on their home computers that will analyze signal data during the processor’s normal idle time. SETI is a NOW architecture. The project has been highly successful, with half a million years of CPU time being accumulated in about 18 months.
For general-use computing, the concept of transparency is very important in distributed systems. As many details about the distributed nature of the network should be hidden as possible. Using remote system resources should require no more effort than using the local system.
Remote procedure calls (RPCs) extend the concept of distributed computing and help provide the necessary transparency for resource sharing. Using RPCs, a computer can invoke a procedure to use the resources available on another computer. The procedure itself resides on the remote machine, but the invocation is done as if the procedure were local to the calling system. RPCs are used by Microsoft’s Distributed Component Object Model (DCOM), the Open Group’s Distributed Computing Environment (DCE), the Common Object Request Broker Architecture (CORBA), and Java’s Remote Method Invocation (RMI). Today’s software designers are leaning toward an object-oriented view of distributed computing, which has fostered the popularity of DCOM, CORBA, and RMI.
9.5 Alternative Parallel Processing Approaches
Entire books have been devoted to particular alternative and advanced architectures. Although we cannot discuss all of them in this brief section, we can introduce you to a few of the more notable systems that diverge from the traditional von Neumann architecture. These systems implement new ways of thinking about computers and computation. They include dataflow computing, neural networks, and systolic processing.
9.5.1 Dataflow Computing
Von Neumann machines exhibit sequential control flow. A program counter determines the next instruction to execute. Data and instructions are segregated. The only way in which data may alter the execution sequence is if the value in the program counter is changed according to the outcome of a statement that references a data value.
In dataflow computing, the control of the program is directly tied to the data itself. It is a simple approach: An instruction is executed when the data necessary for execution become available. Therefore, the actual order of instructions has no bearing on the order in which they are eventually executed. Execution flow is completely determined by data dependencies. There is no concept of shared data storage in these systems, and there are no program counters to control execution. Data flows continuously and is available to multiple instructions at the same time. Each instruction is considered to be a separate process. Instructions do not reference memory; instead, they reference other instructions. Data is passed from one instruction to the next.
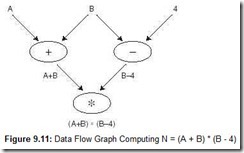
We can understand the computation sequence of a dataflow computer by examining its data flow graph. In a data flow graph, nodes represent instructions, and arcs indicate data dependencies between instructions. Data flows through this graph in the form of data tokens. When an instruction has all of the data tokens it needs, the node fires. When a node fires, it consumes the data tokens, performs the required operation, and places the resulting data token on an output arc. This idea is illustrated in Figure 9.11.
The data flow graph shown in Figure 9.11 is an example of a static dataflow architecture in which the tokens flow through the graph in a staged pipelined fashion. In dynamic dataflow architectures, tokens are tagged with context information and are stored in a memory. During every clock cycle, memory is searched for the set of tokens necessary for a node to fire. Nodes fire only when they find a complete set of input tokens within the same context.
Programs for dataflow machines must be written in languages that are specifically designed for this type of architecture; these include VAL, Id, SISAL, and LUCID. Compilation of a dataflow program results in a data flow graph much like the one illustrated in Figure 9.11. The tokens propagate along the arcs as the program executes.
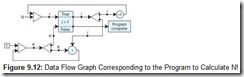
Consider the sample code that calculates N!:
(initial j <- n; k <- 1 while j > 1 do new k <- k * j; new j <- j - 1; return k)
The corresponding data flow graph is shown in Figure 9.12. The two values, N and 1, are fed into the graph. N becomes token j. When j is compared to 1, if it is greater than 1, the j token is passed through and doubled, with one copy of the token passed to the “-1 node” and one copy passed to the multiply node. If j is not greater than 1, the value of k is passed through as the output of the program. The multiply node can only fire when both a new j token and a new k token are available. The “right facing” triangles that N and 1 feed into are “merge” nodes and fire whenever either input is available. Once N and 1 are fed into the graph, they are “used up” and the new j and new k values cause the merge nodes to fire.
Al Davis, of the University of Utah, built the first dataflow machine in 1977. The first multiprocessor dataflow system (containing 32 processors) was developed at CERT-ONERA in France in 1979. The University of Manchester created the first tagged-token dataflow computer in 1981. The commercially available Manchester tagged dataflow model is a powerful dataflow paradigm based on dynamic tagging. This particular architecture is described as tagged because data values (tokens) are tagged with unique identifiers to specify the current iteration level. The tags are required because programs can be reentrant, meaning the same code can be used with different data. By comparing the tags, the system determines which data to use during each iteration. Tokens that have matching tags for the same instruction cause the node to fire.
A loop serves as a good example to explain the concept of tagging. A higher level of concurrency can be achieved if each iteration of the loop is executed in a separate instance of a subgraph. This subgraph is simply a copy of the graph. However, if there are many iterations of the loop, there will be many copies of the graph. Rather than copying the graph, it would be more efficient to share the nodes among different instances of a graph. The tokens for each instance must be identifiable, and this is done by giving each of them a tag. The tag for each token identifies the instance to which it belongs. That way, tokens intended for, say, the third iteration, cannot cause nodes for the fourth iteration to fire.
The architecture of a dataflow machine consists of a number of processing elements that must communicate with each other. Each processing element has an enabling unit that sequentially accepts tokens and stores them in memory. If the node to which this token is addressed fires, the input tokens are extracted from memory and are combined with the node itself to form an executable packet. The processing element’s functional unit computes any necessary output values and combines them with destination addresses to form more tokens. These tokens are then sent back to the enabling unit, at which time they may enable other nodes. In a tagged-token machine, the enabling unit is split into two separate stages: the matching unit and the fetching unit. The matching unit stores tokens in its memory and determines whether an instance of a given destination node has been enabled. In tagged architectures, there must be a match of both the destination node address and the tag. When all matching tokens for a node are available, they are sent to the fetching unit, which combines these tokens with a copy of the node into an executable packet, which is then passed on to the functional unit.
Because data drives processing on dataflow systems, dataflow multiprocessors do not suffer from the contention and cache coherency problems that are so vexing to designers of control driven multiprocessors. It is interesting to note that von Neumann, whose name is given to the von Neumann bottleneck in traditional computer architectures, studied the possibility of data-driven architectures similar in nature to dataflow machines. In particular, he studied the feasibility of neural networks, which are data-driven by nature and discussed in the next section.
9.5.2 Neural Networks
Traditional architectures are quite good at fast arithmetic and executing deterministic programs. However, they are not so good at massively parallel applications, fault tolerance, or adapting to changing circumstances. Neural networks, on the other hand, are useful in dynamic situations where we can’t formulate an exact algorithmic solution, and where processing is based on an accumulation of previous behavior.
Whereas von Neumann computers are based on the processor/memory structure, neural networks are based on the parallel architecture of human brains. They attempt to implement simplified versions of biological neural networks. Neural networks represent an alternative form of multiprocessor computing with a high degree of connectivity and simple processing elements. They can deal with imprecise and probabilistic information and have mechanisms that allow for adaptive interaction between the processing elements. Neural networks (or neural nets), like biological networks, can learn from experience.
Neural network computers are composed of a large number of simple processing elements that individually handle one piece of a much larger problem. Simply stated, a neural net consists of processing elements (PEs), which multiply inputs by various sets of weights, yielding a single output value. The actual computation involved is deceptively easy; the true power of a neural network comes from the parallel processing of the interconnected PEs and the adaptive nature of the sets of weights. The difficulties in creating neural networks lie in determining which neurons (PEs) should be connected to which, what weights should be placed on the edges, and the various thresholds that should be applied to these weights. Furthermore, as a neural network is learning, it can make a mistake. When it does, weights and thresholds must be changed to compensate for the error. The network’s learning algorithm is the set of rules that governs how these changes are to be made.
Neural networks are known by many different names, including connectionist systems, adaptive systems, and parallel distributed processing systems. These systems are particularly powerful when a large database of previous examples can be used by the neural net to learn from prior experiences. They have been used successfully in a multitude of real world applications including quality control, weather forecasting, financial and economic forecasting, speech and pattern recognition, oil and gas exploration, health care cost reduction, bankruptcy prediction, machine diagnostics, securities trading, and targeted marketing. It is important to note that each of these neural nets has been specifically designed for a certain task, so we cannot take a neural network designed for weather forecasting and expect it to do a good job for economic forecasting.
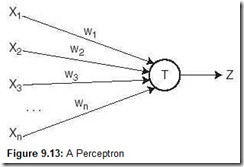
The simplest example of a neural net is the perceptron, a single trainable neuron. A perceptron produces a Boolean output based on the values that it receives from several inputs. A perceptron is trainable because its threshold and input weights are modifiable. Figure 9.13 shows a perceptron with inputs x1, x2, . . . , xn, which can be Boolean or real values. Z is the Boolean output. The wi‘s represent the weights of the edges and are real values. T is the real-valued threshold. In this example, the output Z is true (1) if the net input, w1x1 + w2x2 + . . . + wnxn, is greater than the threshold T. Otherwise, Z is zero.
A perceptron produces outputs for specific inputs according to how it is trained. If the training is done correctly, we should be able to give it any input and get reasonably correct output. The perceptron should be able to determine a reasonable output even if it has never before seen a particular set of inputs. The “reasonableness” of the output depends on how well the perceptron is trained.
Perceptrons are trained by use of either supervised or unsupervised learning algorithms. Supervised learning assumes prior knowledge of correct results, which are fed to the neural net during the training phase. While it is learning, the neural net is told whether its final state is correct. If the output is incorrect, the network modifies input weights to produce the desired results. Unsupervised learning does not provide the correct output to the network during training. The network adapts solely in response to its inputs, learning to recognize patterns and structure in the input sets. We assume supervised learning in our examples.
The best way to train a neural net is to compile a wide range of examples that exhibit the very characteristics in which you are interested. A neural network is only as good as the training data, so great care must be taken to select a sufficient number of correct examples. For example, you would not expect a small child to be able to identify all birds if the only bird he had ever seen was a chicken. Training takes place by giving the perceptron inputs and then checking the output. If the output is incorrect, the perceptron is notified to change its weights and possibly the threshold value to avoid the same mistake in the future. Moreover, if we show a child a chicken, a sparrow, a duck, a hawk, a pelican, and a crow, we cannot expect the child to remember the similarities and differences after seeing them only once. Similarly, the neural net must see the same examples many times in order to infer the characteristics of the input data that you seek.
A perceptron can be trained to recognize the logical AND operator quite easily. Assuming there are n inputs, the output should be 1 only if all inputs are equal to 1. If the threshold of the perceptron is set to n, and the weights of all edges are set to 1, the correct output is given. On the other hand, to compute the logical OR of a set of inputs, the threshold simply needs to be set to 1. In this way, if at least one of the inputs is 1, the output will be 1.
For both the AND and OR operators, we know what the values for the threshold and weights should be. For complex problems, these values are not known. If we had not known the weights for AND, for example, we could start the weights at 0.5 and give various inputs to the perceptron, modifying the weights as incorrect outputs were generated. This is how neural net training is done. Typically, the network is initialized with random weights between -1 and 1. Correct training requires thousands of steps. The training time itself depends on the size of the network. As the number of perceptrons increases, the number of possible “states” also increases.
Let’s consider a more sophisticated example, that of determining whether a tank is hiding in a photograph. A neural net can be configured so that each output value correlates to exactly one pixel. If the pixel is part of the image of a tank, the net should output a one; otherwise, the net should output a zero. The input information would most likely consist of the color of the pixel. The network would be trained by feeding it many pictures with and without tanks. The training would continue until the network correctly identified whether the photos included tanks.
The U.S. military conducted a research project exactly like the one we just described. One hundred photographs were taken of tanks hiding behind trees and in bushes, and another 100 photographs were taken of ordinary landscape with no tanks. Fifty photos from each group were kept “secret,” and the rest were used to train the neural network. The network was initialized with random weights before being fed one picture at a time. When the network was incorrect, it adjusted its input weights until the correct output was reached. Following the training period, the 50 “secret” pictures from each group of photos were fed into the network. The neural network correctly identified the presence or absence of a tank in each photo.
The real question at this point has to do with the training-had the neural net actually learned to recognize tanks? The Pentagon’s natural suspicion led to more testing. Additional photos were taken and fed into the network, and to the researchers’ dismay, the results were quite random. The neural net could not correctly identify tanks within photos. After some investigation, the researchers determined that in the original set of 200 photos, all photos with tanks had been taken on a cloudy day, whereas the photos with no tanks had been taken on a sunny day. The neural net had properly separated the two groups of pictures, but had done so using the color of the sky to do this rather than the existence of a hidden tank. The government was now the proud owner of a very expensive neural net that could accurately distinguish between sunny and cloudy days!
This is a great example of what many consider the biggest issue with neural networks. If there are more than 10 to 20 neurons, it is impossible to understand how the network is arriving at its results. One cannot tell if the net is making decisions based on correct information, or, as in the above example, something totally irrelevant. Neural networks have a remarkable ability to derive meaning and extract patterns from data that are too complex to be analyzed by human beings. However, some people trust neural networks to be experts in their area of training. Neural nets are used in such areas as sales forecasting, risk management, customer research, undersea mine detection, facial recognition, and data validation. Although neural networks are promising, and the progress made in the past several years has led to significant funding for neural net research, many people are hesitant to put confidence in something that no human being can completely understand.
9.5.3 Systolic Arrays
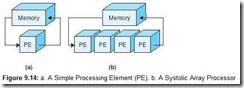
Systolic array computers derive their name from drawing an analogy to how blood rhythmically flows through a biological heart. They are a network of processing elements that rhythmically compute data by circulating it through the system. Systolic arrays are a variation of SIMD computers that incorporates large arrays of simple processors that use vector pipelines for data flow, as shown in Figure 9.14b. Since their introduction in the 1970s, they have had a significant impact on special-purpose computing. One well-known systolic array is CMU’s iWarp processor, which was manufactured by Intel in 1990. This system consists of a linear array of processors connected by a bidirectional data bus.
Although Figure 9.14b illustrates a one-dimensional systolic array, two-dimensional arrays are not uncommon. Three-dimensional arrays are becoming more prevalent with the advances in VLSI technology.
Systolic arrays employ a high degree of parallelism (through pipelining) and can sustain a very high throughput. Connections are typically short, and the design is simple and thus highly scalable. They tend to be robust, highly compact, efficient, and cheap to produce. On the down side, they are highly specialized and thus inflexible as to the types and sizes of problems they can solve.
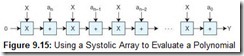
A good example of using systolic arrays can be found in polynomial evaluation. To evaluate the polynomial y = a0 + a1x + a2x2 + . . . + akxk, we can use Horner’s Rule:
y = ((((anx + an-1) x x + an-2) x x + an-3) x x …. a1) x x + a0
A linear systolic array, in which the processors are arranged in pairs, can be used to evaluate a polynomial using Horner’s Rule, as shown in Figure 9.15. One processor multiplies its input by x and passes the result to the right. The next processor adds aj and passes the result to the right. After an initial latency of 2n cycles to get started, a polynomial is computed in every cycle.
Systolic arrays are typically used for repetitive tasks, including Fourier transformations, image processing, data compression, shortest path problems, sorting, signal processing, and various matrix computations (such as inversion and multiplication). In short, systolic array computers are suitable for computational problems that lend themselves to a parallel solution using a large number of simple processing elements.
Chapter Summary
This chapter has presented an overview of some important aspects of multiprocessor and multicomputer systems. These systems provide a means of solving otherwise unmanageable problems in an efficient manner.
The RISC versus CISC debate is becoming increasingly more a comparison of chip architectures, not ISAs. What really matters is program execution time, and both RISC and CISC designers will continue to improve performance.
Flynn’s taxonomy categorizes architectures depending on the number of instructions and data streams. MIMD machines should be further divided into those that use shared memory and those that do not.
The power of today’s digital computers is truly astounding. Internal processor parallelism has contributed to this increased power through superscalar and superpipelined architectures. Originally, processors did one thing at a time, but it is now common for them to perform multiple concurrent operations. Vector processors support vector operations, whereas MIMD machines incorporate multiple processors.
SIMD and MIMD processors are connected through interconnection networks. Shared memory multiprocessors treat the collection of physical memories as a single entity, whereas distributed memory architectures allow a processor sole access to its memory. Either approach allows the common user to have supercomputing capability at an affordable price. The most popular multiprocessor architectures are MIMD, shared memory, bus-based systems.
Some highly complex problems cannot be solved using our traditional model of computation. Alternative architectures are necessary for specific applications. Dataflow computers allow data to drive computation, rather than the other way around. Neural networks learn to solve problems of the highest complexity. Systolic arrays harness the power of small processing elements, pushing data throughout the array until the problem is solved.
Review of Essential Terms and Concepts
-
Why was the RISC architecture concept proposed?
-
Why is a RISC processor easier to pipeline than a CISC processor?
-
Describe how register windowing makes procedure calls more efficient.
-
Flynn’s taxonomy classifies computer architectures based on two properties. What are they?
-
We propose adding a level to Flynn’s taxonomy. What is the distinguishing characteristic of computers at this higher level?
-
Do all programming problems lend themselves to parallel execution? What is the limiting factor?
-
How is a superscalar design different from a superpipelined design?
-
In what way does a VLIW design differ from a superpipelined design?
-
What are the similarities and differences between EPIC and VLIW?
-
Explain the limitation inherent in a register-register vector processing architecture.
-
Give two reasons for the efficiency of vector processors.
-
Draw pictures of the six principal interconnection network topologies.
-
There are three types of shared memory organizations. What are they?
-
Describe one of the cache consistency protocols discussed in this chapter.
-
What is SETI and how does it use the distributed computing model?
-
What differentiates dataflow architectures from “traditional” computational architectures?
-
What is reentrant code?
-
What is the fundamental computing element of a neural network?
-
Describe how neural networks “learn.”
-
Through what metaphor do systolic arrays get their name? Why is the metaphor fairly accurate?
-
What kinds of problems are suitable for solution by systolic arrays?
Exercises
-
Hints and Answers Why do RISC machines operate on registers?
-
Which characteristics of RISC systems could be directly implemented in CISC systems? Which characteristics of RISC machines could not be implemented in CISC machines (based on the defining characteristics of both architectures as listed in Table 9.1)?
-
Hints and Answers What does the “reduced” in reduced instruction set computer really mean?
-
Suppose a RISC machine uses overlapping register windows with:
10 global registers
6 input parameter registers
10 local registers
6 output parameter registers
How large is each overlapping register window?
-
Hints and Answers A RISC processor has 8 global registers and 10 register windows. Each window has 4 input registers, 8 local registers, and 4 output registers. How many total registers are in this CPU? (Hint: Remember, due to the circular nature of the windows, the output registers of the last window are shared as the input registers of the first window.)
-
A RISC processor has 152 total registers, with 12 designated as global registers. The 10 register windows each have 6 input registers and 6 output registers. How many local registers are in each register window set?
-
A RISC processor has 186 total registers, with 18 globals. There are 12 register windows, each with 10 locals. How many input/output registers are in each register window?
-
Suppose a RISC machine uses overlapping register windows for passing parameters between procedures. The machine has 298 registers. Each register window has 32 registers, of which 10 are global variables and 10 are local variables. Answer the following:
-
How many registers would be available for use by input parameters?
-
How many registers would be available for use by output parameters?
-
How many register windows would be available for use?
-
By how much would the current window pointer (CWP) be incremented at each procedure call?
-
-
Hints and Answers Recall our discussions from Chapter 8 regarding context switches. These occur when one process stops using the CPU and another process begins. In this sense, register windows could be viewed as a potential weakness of RISC. Explain why this is the case.
-
Suppose that a RISC machine uses 5 register windows.
-
How deep can the procedure calls go before registers must be saved in memory? (That is, what is the maximum number of “active” procedure calls that can be made before we need to save any registers in memory?)
-
Suppose two more calls are made after the maximum value from part (a) is reached. How many register windows must be saved to memory as a result?
-
Now suppose that the most recently called procedure returns. Explain what occurs.
-
Now suppose one more procedure is called. How many register windows need to be stored in memory?
-
-
In Flynn’s taxonomy:
-
Hints and Answers What does SIMD stand for? Give a brief description and an example.
-
What does MIMD stand for? Give a brief description and an example.
-
-
Flynn’s taxonomy consists of four primary models of computation. Briefly describe each of the categories and give an example of a high-level problem for which each of these models might be used.
-
Hints and Answers Explain the difference between loosely coupled and tightly coupled architectures.
-
Describe the characteristics of MIMD multiprocessors that distinguish them from multicomputer systems or computer networks.
-
How are SIMD and MIMD similar? How are they different? Note, you are not to define the terms, but instead compare the models.
-
What is the difference between SIMD and SPMD?
-
Hints and Answers For what type of program-level parallelism (data or control) is SIMD best suited? For what type of program-level parallelism is MIMD best suited?
-
Describe briefly and compare the VLIW and superscalar models with respect to instruction-level parallelism.
-
Hints and Answers Which model, VLIW or superscalar, presents the greater challenge for compilers? Why?
-
Hints and Answers Compare and contrast the superscalar architecture to the VLIW architecture.
-
Hints and Answers Why are distributed systems desirable?
-
What is the difference between UMA and NUMA?
-
Hints and Answers What are the main problems with using crossbars for interconnection networks? What problems do buses present in interconnection networks?
-
Given the following Omega network, which allows 8 CPUs (P0 through P7) to access 8 memory modules (M0 through M7):
-
Show how the following connections through the network are achieved (explain how each switch must be set). Refer to the switches as 1A, 2B, etc.:
-
P0 ® M2
-
P4 ® M4
-
P6 ® M3
-
-
Can these connections occur simultaneously or do they conflict? Explain.
-
List a processor-to-memory access that conflicts (is blocked) by the access P0 ® M2 that is not listed in part (a).
-
List a processor-to-memory access that is not blocked by the access P0 ® M2 and is not listed in part (a).
-
-
Hints and Answers Describe write-through and write-back cache modification as they are used in shared memory systems, and the advantages and disadvantages of both approaches.
-
Should the memory of a dataflow system be associative or address-based? Explain.
-
Hints and Answers Do neural networks process information sequentially? Explain.
-
Compare and contrast supervised learning and unsupervised learning with regard to neural networks.
-
Hints and Answers Describe the process of supervised learning in neural networks from a mathematical perspective.
-
These two questions deal with a single perceptron of a neural network.
-
The logical NOT is a little trickier than AND or OR, but can be done. In this case, there is only one Boolean input. What would the weight and threshold be for this perceptron to recognize the logical NOT operator?
-
Show that it is not possible to solve the binary XOR problem for two inputs, x1 and x2, using a single perceptron.
-
-
Explain the differences between SIMD and systolic array computing when the systolic array is one-dimensional.
-
With respect to Flynn’s taxonomy, where do systolic arrays fit? What about clusters of workstations?
-
Indicate whether each of the following applies to CISC or RISC by placing either a C (for CISC) or an R (for RISC) in the blank.
-
_____ Simple instructions averaging one clock cycle to execute.
-
_____ Single register set.
-
_____ Complexity is in the compiler.
-
_____ Highly pipelined.
-
_____ Any instruction can reference memory.
-
_____ Instructions are interpreted by the microprogram.
-
_____ Fixed length, easily decoded instruction format.
-
_____ Highly specialized, infrequently used instructions.
-
_____ Use of overlapping register windows.
-
_____ Relatively few addressing modes.
-