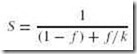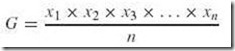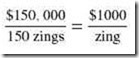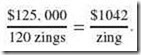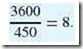electric equipment

Chapter 10: Performance Measurement and Analysis

10.1 Introduction

If you can’t measure it, you can’t manage it.

—Peter Drucker

Figures are not always facts.

—American saying

The two quotations with which we introduce this chapter highlight the dilemma of computer performance evaluation. One must have quantitative tools with which to gauge performance, but how can one be certain that the tools chosen for the task meet the objectives of the assessment? In fact, one cannot always be certain that this is the case. Furthermore, system purveyors are strongly motivated to slant otherwise truthful numbers so that their brand of system looks better than its competitors.

You can defend yourself against most statistical chicanery by cultivating a thorough understanding of the basics of computer performance assessment. The foundation that we present in this chapter will be useful to you whether you are called upon to help select a new system or are trying to improve the performance of an existing system.

This chapter also presents some of the factors that affect the performance of processors, programs, and magnetic disk storage. The ideas presented in these sections are of primary concern in system tuning. Good system performance tools (usually supplied by the manufacturer) are an indispensable aid in keeping a system running at its best. After completing this chapter, you will know what to look for in system tuning reports, and how each piece of information fits into the big picture of overall system performance.

10.2 The Basic Computer Performance Equation

You have seen the basic computer performance equation several times in previous chapters. This equation, which is fundamental to measuring computer performance, measures the CPU time:

where the time per program is the required CPU time. Analysis of this equation reveals that CPU optimization can have a dramatic effect on performance. We have already discussed several ways to increase performance based on this equation. RISC machines try to reduce the number of cycles per instruction, and CISC machines try to reduce the number of instructions per program. Vector processors and parallel processors also increase performance by reducing CPU time. Other ways to improve CPU performance are discussed later in this chapter.

CPU optimization is not the only way to increase system performance. Memory and I/O also weigh heavily on system throughput. The contribution of memory and I/O, however, is not accounted for in the basic equation. For increasing the overall performance of a system, we have the following options:

• CPU optimization-Maximize the speed and efficiency of operations performed by the CPU (the performance equation addresses this optimization).

• Memory optimization-Maximize the efficiency of a code’s memory management.

• I/O optimization-Maximize the efficiency of input/output operations.

An application whose overall performance is limited by one of the above is said to be CPU bound, memory bound, or I/O bound, respectively. In this chapter, we address optimization at all three levels.

Before examining optimization techniques, we first ask you to recall Amdahl’s Law, which places a limit on the potential speedup one can obtain by any means. The equation states that the performance improvement to be gained from using some faster mode of execution is limited by the fraction of the time that the faster mode is used:

where S is the speedup; f is the fraction of work performed by the faster component (or the enhancement); and k is the speedup of a new component (or the enhancement).

Accordingly, the most dramatic improvement in system performance is realized when the performance of the most frequently used components is improved. In short, our efforts at improving performance reap the greatest rewards by making the common case faster. Knowing whether a system or application is CPU bound, memory bound, or I/O bound is the first step toward improving system performance. Keep these ideas in mind as you read the discussions on improving performance. We begin with a discussion of the various measures of overall system performance, and then describe factors relating to the performance of individual system components. Before beginning any of these topics, however, we first introduce the necessary mathematical concepts for understanding general computer performance measurement.

10.3 Mathematical Preliminaries

Computer performance assessment is a quantitative science. Mathematical and statistical tools give us many ways in which to rate the overall performance of a system and the performance of its constituent components. In fact, there are so many ways to quantify system performance that selecting the correct statistic becomes a challenge in itself. In this section, we describe the most common measures of “average” computer performance and then provide situations where the use of each is appropriate and inappropriate. In the second part of this section, we present other ways in which quantitative information can be misapplied through erroneous reasoning. Before proceeding, however, a few definitions are in order.

Measures of system performance depend on one’s point of view. A computer user is most concerned with response time: How long does it take for the system to carry out a task? System administrators are most concerned with throughput: How many concurrent tasks can the system carry out without adversely affecting response time? These two points of view are inversely related. Specifically, if a system carries out a task in k seconds, its throughput is 1/k of these tasks per second.

In comparing the performance of two systems we measure the time that it takes for each system to perform the same amount of work. If the same program is run on two systems, System A and System B, System A is n times as fast as System B if:

System A is x% faster than System B if:

Consider the performance of two race cars. Car A completes a 10-mile run in 3 minutes, and Car B completes the same 10-mile course in 4 minutes. Using our performance formulas, the performance of Car A is 1.25 times as fast as Car B:

Car A is also 25% faster than Car B:

These formulas are useful in comparing the average performance of one system with the average performance of another. However, the number that we end up with is as much dependent on our definition of “average” as it is on the actual performance of the systems.

10.3.1 What the Means Mean

The science of statistics tells us that if we want meaningful information, we must conduct an adequate number of tests in order to justify making inferences based on the results of the tests. The greater the variability in the test, the larger the sample size must be. After we have conducted a “sufficient” number of tests, we are left with the task of combining, or averaging, the data in a way that makes sense, forming a concise measure of central tendency. Measures of central tendency indicate to us the expected behavior of the sampled system (population). But not all methods of averaging data are equal. The method we choose depends on the nature of the data itself as well as the statistical distribution of the test results.

The Arithmetic Mean

The arithmetic mean is the one with which everyone is most familiar. If we have five measurements, and we add them together and divide by five, then the result is the arithmetic mean. When people refer to the average results of some metric- for example, the cost of gasoline in the past year-they are usually referring to the arithmetic average of the price sampled at some given frequency.

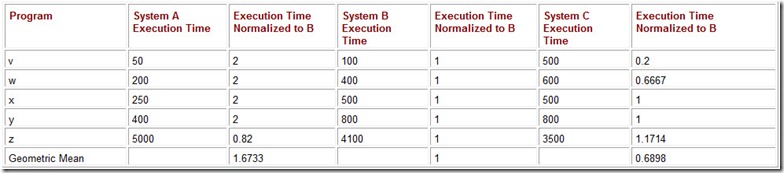
An arithmetic average should not be used when the data are highly variable or skewed toward lower or higher values. Consider the performance numbers for three computers, as shown in Table 10.1. The values given are the running times for five programs as measured on each of the three systems. By looking at the running times, the performance of these three systems is obviously different. This fact is completely hidden if we report only the arithmetic average of the running times.

Table 10.1: The Arithmetic Average Running Time in Seconds of Five Programs on Three Systems

When it is used properly, the weighted arithmetic mean improves on the arithmetic average because it can give us a clear picture of the expected behavior of the system. If we have some indication of how frequently each of the five programs are run during the daily processing on these systems, we can use the execution mix to calculate relative expected performance for each of the systems. The weighted average is found by taking the products of the frequency with which the program is run and its running time. Averaging the weighted running times produces the weighted arithmetic mean.

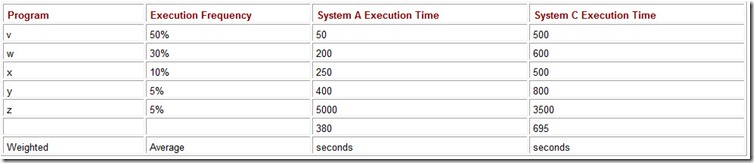
The running times for System A and System C from Table 10.1 are restated in Table 10.2. We have supplemented the running times with execution frequencies for each of the programs. For example, on System A, for every 100 of the combined executions of programs v, w, x, y, and z, program y runs 5 times. The weighted average of the execution times for these five programs running on System A is:

Table 10.2: The Execution Mix for Five Programs on Two Systems and the Weighted Average of the Running Times

50 x 0.5 + 200 x 0.3 + 250 x 0.1 + 400 x 0.05 + 5000 x 0.05 = 380.

A similar calculation reveals that the weighted average of the execution times for these five programs running on System B is 695 seconds. Using the weighted average, we now see clearly that System A is about 83% faster than System C for this particular workload.

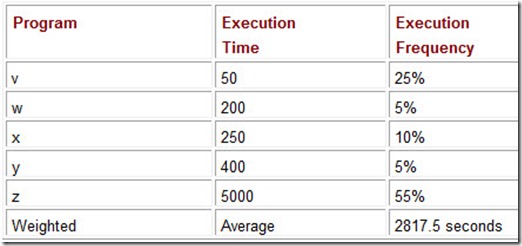
One of the easiest ways to get into trouble with weighted averages is using assumptions that don’t hold over time. Let’s assume the computer workload profile for a particular company exhibits the execution mix shown in Table 10.2. Based on this information, the company purchases System A rather than System C. Suppose a sharp user, we can call him Wally, figures out that Program z will give him the same results as running Program v, and then using its result as an input to Program w. Furthermore, because Program z takes such a long time to run, Wally has a good excuse to take an extra coffee break. Before long, word of Wally’s discovery spreads throughout the office and practically everyone in Wally’s unit begins capitalizing on his idea. Within days, the workload profile of System A looks like the one shown in Table 10.3. The folks in the executive suite are certain to be at a loss to explain why their brand new system is suddenly offering such poor performance.

Table 10.3: The Weighted Average Running Times for System A Using a Revised Execution Mix

The Geometric Mean

We know from the previous discussion that we cannot use the arithmetic mean if our measurements exhibit a great deal of variability. Further, unless we have a clear view of a static and representative workload, the weighted arithmetic mean is of no help either. The geometric mean gives us a consistent number with which to perform comparisons regardless of the distribution of the data.

Formally, the geometric mean is defined as the nth root of the product of the n measurements. It is represented by the following formula:

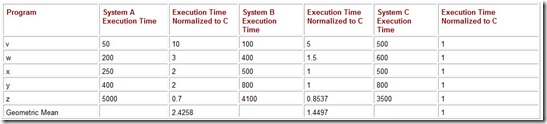
The geometric mean is more helpful to us than the arithmetic average when we are comparing the relative performance of two systems. Performance results are easy to compare when they are stated in relation to the performance of a common machine used only as a reference. We say that the systems under evaluation are normalized to the reference machine when we take the ratio of the run time of a program on the reference machine to the run time of the same program on the system being evaluated.

To find the geometric mean of the normalized ratios we take the nth root of the product of the n ratios. The geometric means for System A and System C normalized to System B are calculated as follows:

The details of this calculation are shown in Table 10.4.

Table 10.4: The Geometric Means for This Sample of Five Programs, Found by Taking the Fifth Root of the Products of the Normalized Execution Times for Each System

One of the nice properties of the geometric mean is that we get the same results regardless of which system we pick for a reference. Table 10.5 shows the results when System C is the reference machine. Notice that the ratio of the geometric means is consistent no matter which system we choose for the reference machine:

Table 10.5: The Geometric Means When System A Is Used for a Reference System

We would find the same ratios if we used System A as a reference.

The geometric mean bears out our intuition concerning the relative performance of System A and System C. By taking the ratios of their geometric means, we see that System A gives a much poorer result than System B. However, the geometric mean is not linear. Although the ratio of the geometric means of System A to System C is 2.43, this does not imply that System C is 2.43 times as fast as System A. This fact is evident by the raw data. So anyone who buys System C thinking that it will give double the performance of System A is sure to be disappointed. Unlike the weighted arithmetic mean, the geometric mean gives us absolutely no help in formulating a statistical expectation of the actual behavior of the systems.

A second problem with the geometric mean is that small values have a disproportionate influence in the overall result. For example, if the makers of System C improve the performance of the fastest (probably simplest) program in the test set by 20%, so that it runs in 400 seconds instead of 500 seconds, the normalized geometric mean improves by over 4.5%. If we improve it by 40% (so that it runs in 300 seconds), the normalized geometric mean improves by over 16%. No matter which program we improve by 20% or 40%, we see the same reduction in the relative geometric mean. One would expect that it’s much more difficult to shave 700 seconds from a large, complex program than it is to pare 200 seconds from the execution of a smaller, simpler program. In the real world (by Amdahl’s Law), it is our largest, most time-consuming programs that have the greatest influence on system performance.

The Harmonic Mean

Neither the geometric mean nor the arithmetic mean is appropriate when our data are expressed as a rate, such as operations per second. For averaging rates or ratios, the harmonic mean should be used. The harmonic mean allows us to form a mathematical expectation of throughput as well as to compare the relative throughput of systems or system components. To find the harmonic mean, we add the reciprocals of the data and then divide this sum into the number of data elements in the sample. Stated mathematically:

H = n ÷ (1/x₁ + 1/x₂ + 1/x₃ + . . . + 1/x_n)

To see how the harmonic mean applies to rates, consider the simple example of an automobile trip. Suppose we make a 30-mile journey, traveling the first 10 miles at 30 miles per hour, the second 10 miles at 40 miles per hour, and the last 10 miles at 60 miles per hour. Taking the arithmetic mean of these rates, the average speed of the trip is 43.3 miles per hour. This is incorrect. The time required to travel the first 10 miles was 1/3 hour. The second 10 miles took 1/4 hour, and the third 10 miles was traveled in 1/6 hour. The total time of the journey was 3/4 hour, making the average speed 30 miles ÷ 3/4 hour = 40 miles per hour. The harmonic mean gives us the correct answer succinctly: 3 ÷ (1/30 + 1/40 + 1/60) = 40 miles per hour.

In order for our example to work out with respect to the average speed over a given distance, we had to be careful that the same amount of distance was covered on each leg of the journey. The harmonic mean would have been the same if the car had traveled 100 miles (instead of 10) at 60 miles per hour. A harmonic mean does not tell us how much work was done, only the average rate at which it was done.

The harmonic mean holds two advantages over the geometric mean. First, a harmonic mean is a suitable predictor of machine behavior. The result, therefore, has usefulness outside the realm of performance comparison. Secondly, more time-consuming programs have greater influence on the harmonic mean than less time-consuming ones. Not only does this fact weigh against “quick fix” optimizations, it also reflects reality. Large, slow tasks have the potential of eating more machine cycles than smaller, faster ones. Consequently, we have more to gain by improving their performance.

As with the geometric mean, the harmonic mean can be used with relative performance ratios. However, the harmonic mean is more sensitive to the choice of the reference machine. In other words, the ratios of the harmonic means are not as consistent as those of the geometric means. Before the geometric mean can be used to compare machine performance, however, a definition of “work” must be established. Later in this chapter, you will see what a slippery idea this is.

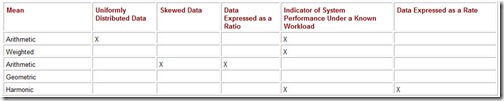
We showed that the arithmetic mean is inappropriate for averaging rates, using an example road trip. It is also incorrect to use the arithmetic mean with results expressed as normalized ratios. The proper application of each of the means that we have presented is summarized in Table 10.6.

Table 10.6: Data Characteristics and Suitability of Means

Occasionally, misapplied statistics turn up in places where we least expect to find them. Misapplication of the means is only one of several pitfalls that lie in the path of equitable and objective system performance assessment.

10.3.2 The Statistics and Semantics

Human nature impels us to cast ourselves and our beliefs in the best way possible. For persons trying to sell their products to us, their motivations are tied to survival as much as ego. It can be exceedingly difficult to see a product in its true light when it is surrounded by the fog of slick presentations and advertisements- even when the product is very good. Readers who have had some exposure to the concepts of rhetorical logic understand the ways in which fallacious reasoning can be used in sales and advertising. A classic example is where an actor “who plays a doctor on TV” recommends a certain remedy for a vexing ailment. In rhetorical logic, this is called the argumentum ad verecundiam, or “appeal to unqualified authority” fallacy. An actor, unless he also has a medical degree, is not qualified to make assertions as to the suitability of any treatment for any malady. Although we don’t often see actors “who play computer scientists on TV” recommending mainframes, some computer vendors’ sales pitches can be a source of considerable amusement for people who know what to watch for.

Computer buyers are often intimidated by the numbers cited in computer sales literature. We have mentioned how averages can be misapplied. Even when the correct statistics are used, they are not easy for many people to understand. The “quantitative” information supplied by vendors always lends an aura of credibility to the vendor’s claims of superior performance. In Section 10.4, we discuss a number of objective measures of computer performance. Reputable vendors cite these measurements without distortion. But even excellent metrics are subject to misuse. In the sections that follow, we present three of the prevalent rhetorical fallacies that you are likely to encounter if you are ever tasked with purchasing new hardware or system software. We supply them as much for your entertainment as for your enlightenment.

Incomplete Information

In early 2002, a full-page advertisement was running in major business and trade magazines. The gist of the ad was, “We ran a test of our product and published the results. Vendor X did not publish results for the same test for his product, therefore, our product is faster.” Huh? All that you really know are the statistics cited in the ad. It says absolutely nothing about the relative performance of the products.

Sometimes, the fallacy of incomplete information takes the form of a vendor citing only the good test results while failing to mention that less favorable test results were also obtained on the same system at the same time. An example of this is the “single figure of merit.” Vendors focus in on a single performance metric that gives their systems a marketing advantage over the competition, when in reality, these individual metrics are not representative of the actual workloads of the systems in question. Another way in which incomplete information manifests itself is when a vendor cites only “peak” performance numbers, omitting the average or more commonly expected case.

Vague Information and Inappropriate Measurements

Imprecise words such as “more,” “less,” “nearly,” “practically,” “almost,” and their synonyms should always raise immediate alarm when cited in the context of assessing the relative performance of systems. If these terms are supported with appropriate data, their use may be justified. However, observant readers may learn that “nearly” can mean “only” a 50% difference in performance between Product A and Product B.

A recent pamphlet extolling a certain brand of system software compounded imprecision with the use of inappropriate and incomparable measurements. The flier said roughly, “Software A and Software B were run using Test X. We have results for Software B running Test Y. We show that Test X is almost equivalent to Test Y. From this, we conclude that Software A is faster.” And by how much are Tests X and Y not equivalent? Is it possible that Test X is contrived to make Software A look better? In this case, not only is the (probably well paid) writer comparing apples to oranges, he or she can’t even say whether the total volume of these fruits amounts to a bushel!

Appeal to Popularity

This fallacy is by far the most common, and usually the hardest to defend against in a crowd (such as a computer procurement committee). The pitch is, “Our product is used by X% of the Fortune 500 list of the largest companies in America.” This often irrefutable fact shows that the company is well established and is probably trustworthy and stable as well. These nonquantitative considerations are indeed important factors in systems and software selection. However, just because X% of the Fortune 500 use the product, it doesn’t mean that the product is suitable for your business. That is a much more complicated matter.

10.4 Benchmarking

Performance benchmarking is the science of making objective assessments of the performance of one system over another. Benchmarks are also useful for assessing performance improvements obtained by upgrading a computer or its components. Good benchmarks enable us to cut through advertising hype and statistical tricks. Ultimately, good benchmarks will identify the systems that provide good performance at the most reasonable cost.

Although the issue of “reasonable” cost is usually self-evident after you’ve done some careful shopping, the matter of “good” performance is elusive, defying all attempts at definition for decades. Yet good performance is one of those things where you “know it when you see it,” and bad performance is certain to make your life miserable until the problem is corrected. In a few words, optimum performance is achieved when a computer system runs your application using the least possible amount of elapsed (or wall clock) time. That same computer system will not necessarily run someone else’s application in the shortest possible time.

Life would be easy for the computer buyer if there were some way to classify systems according to a single performance number, or metric. The obvious advantage of this approach is that people with little or no understanding of computers would know when they were getting good value for their money. If we had a simple metric, we could use a price-performance ratio to indicate which system was the best buy.

For example, let’s define a fictional all-encompassing system metric called a “zing.” A $150,000 system offering 150 zings would be a better buy than a $125,000 system offering 120 zings. The price-performance ratio of the first system is:

MIPS . . . OR . . . OOPS?

During the 1970s and 1980s competition was fierce between two leading computer makers: IBM and Digital Equipment Corporation (DEC). Although DEC did not manufacture huge mainframe systems, its largest systems were suitable for the same customers as might be served by IBM’s smaller systems.

To help market their brand-new VAX 11/780, DEC engineers ran some small synthetic benchmark programs on an IBM 370/158 and on their VAX. IBM had traditionally marketed the 370/158 as a “1 MIPS” machine. So when the benchmarks ran in the same elapsed time on the VAX 11/780, DEC began selling their system as a competitive “1 MIPS” system.

The VAX 11/780 was a commercial success. The system was so popular that it became the standard 1 MIPS system. For many years, the VAX 11/780 was the reference system for numerous benchmarks. The results of these benchmarks could be extrapolated to infer an “approximate MIPS” rating for whatever system was tested.

There is no doubt that the VAX 11/780 had comparable computing power to that of the IBM 370/158. But the notion of it being a “1 MIPS” machine didn’t hold up under closer scrutiny. It turns out that to run the benchmarks, the VAX 11/780 executed only about 500,000 machine instructions, owing to its particular instruction set architecture. Thus, the “1 MIPS standard system” was, in fact, a 0.5 MIPS system, after all. DEC subsequently marketed its machines by specifying VUPs (Vax Unit of Performance), which indicates the relative speed of a machine to the VAX 11/780.

while the second is:

The question becomes whether you can live with 120 zings and save $25,000 or if it is better to buy the “large economy size” knowing it will be a while before you exhaust the system’s capacity.

The trouble with this approach is that there can be no universal measure of computer performance, such as “zings,” that is applicable to all systems under all types of workloads. So if you are looking for a system to handle heavy (I/O bound) transaction processing, such as an airline reservation system, you should be more concerned with I/O performance than with CPU speed. Similarly, if your system will be tasked with computationally intense (CPU bound) applications such as weather forecasting or computer-aided drafting, your main focus should be on CPU power rather than on I/O.

10.4.1 Clock Rate, MIPS, and FLOPS

CPU speed, by itself, is a misleading metric that (unfortunately) is most often used by computer vendors touting their systems’ alleged superiority to all others. In architecturally identical systems, a CPU running at double the clock speed of another is likely to give better CPU throughput. But when comparing offerings from different vendors, the systems will probably not be architecturally identical. (Otherwise, neither could claim a competitive performance edge over another.)

A widely cited metric related to clock rate is the millions of instructions per second (MIPS) metric. (Many people, however, believe MIPS actually stands for “Meaningless Indicators of Performance for Salesmen”!) This measures the rate at which the system can execute a typical mix of floating point and integer arithmetic instructions, as well as logical operations. Again, the greatest weakness in this metric is that different machine architectures often require a different number of machine cycles to carry out a given task. The MIPS metric does not take into account the number of instructions necessary to complete a specific task.

The most glaring contrast can be seen when we compare RISC systems to CISC systems. Let’s say that we ask both of these systems to perform an integer division operation. The CISC system may carry out 20 binary machine instructions before delivering a final answer. The RISC system may execute 60 instructions. If both of these systems deliver the answer in one second, the MIPS rating of the RISC system would be triple that of the CISC system. Can we honestly say that the RISC system is three times faster than the CISC system? Of course not: In both cases we received our answer in one second.

There is a similar problem with the FLOPS (floating-point operations per second) metric. Megaflops or MFLOPS is a metric that was originally used in describing the power of supercomputers, but is now cited in personal computer literature. The FLOPS metric is even more vexing than the MIPS metric because there is no agreement as to what constitutes a floating-point operation. In Chapter 2, we explained how computers perform multiplication and division operations through a series of partial products, arithmetic shifts, and additions. During each of these primitive operations, floating-point numbers are manipulated. So can we say that calculating an intermediate partial sum is a floating-point operation? If so, and our metric is FLOPS, then we punish the vendor who uses efficient algorithms. Efficient algorithms arrive at the same result using fewer steps. If the amount of time consumed in finding the answer is the same amount of time consumed using less efficient algorithms, the FLOPS rate of the more efficient system is lower. If we say we’re not going to count partial-sum addition steps, then how can we justify counting other floating-point addition operations? Furthermore, some computers use no floating-point instructions at all. (Early Cray supercomputers and IBM PCs emulated floating-point operations using integer routines.) Because the FLOPS metric takes into account only floating-point operations, based solely on this metric, these systems would be utterly worthless! Nevertheless, MFLOPS, like MIPS, is a popular metric with marketing people because it sounds like a “hard” value and represents a simple and intuitive concept.

Despite their shortcomings, clock speed, MIPS, and FLOPS can be useful metrics in comparing relative performance across a line of similar computers offered by the same vendor. So if a vendor offers to upgrade your system from its present x MIPS rating to a 2x MIPS rating, you have a fairly good idea of the performance improvement that you will be getting for your money. In fact, a number of manufacturers have their own set of metrics for this singular purpose. Ethical salespeople will avoid using their companies’ proprietary metrics to characterize their competitors’ systems. When one manufacturer’s proprietary metrics are used to describe the performance of competing systems, potential customers have no way of knowing whether the proprietary metric is contrived to focus on the strong points of a particular type of system, while ignoring its weaknesses.

Clearly, any metric that is dependent upon a particular system’s organization or its instruction set architecture misses the point of what computer buyers are looking for. They need some objective means of knowing which system offers the maximum throughput for their workloads at the lowest cost.

10.4.2 Synthetic Benchmarks – Whetstone, Linpack, and Dhrystone

Computer researchers have long sought to define a single benchmark that would allow fair and reliable performance comparisons yet be independent of the organization and architecture of any type of system. The quest for the ideal performance measure started in earnest in the late 1980s. The prevailing idea at the time was that one could independently compare the performance of many different systems through a standardized benchmarking application program. It follows that one could write a program using a third-generation language (such as C), compile it and run it on various systems, and then measure the elapsed time for each run of the program on various systems. The resulting execution time would lead to a single performance metric across all of the systems tested. Performance metrics derived in this manner are called synthetic benchmarks, because they don’t necessarily represent any particular workload or application. Three of the better-known synthetic benchmarks are the Whetstone, Linpack, and Dhrystone metrics.

The Whetstone benchmarking program was published in 1976 by Harold J. Curnow and Brian A. Wichman of the British National Physical Laboratory. Whetstone is floating-point intensive, with many calls to library routines for computation of trigonometric and exponential functions. Results are reported in KiloWhetstone Instructions per Second (KWIPS) or Mega-Whetstone Instructions per Second (MWIPS).

Another source for floating-point performance is the Linpack benchmark. Linpack, a contraction of LINear algebra PACKage, is a collection of subroutines called Basic Linear Algebra Subroutines (BLAS), which solves systems of linear equations using double-precision arithmetic. Jack Dongarra, Jim Bunch, Cleve Moler, and Pete Stewart of the Argonne National Laboratory developed Linpack in 1984 to measure the performance of supercomputers. It was originally written in FORTRAN 77 and has subsequently been rewritten in C and Java. Although it has some serious shortcomings, one of the good things about Linpack is that it sets a standard measure for FLOPS. A system that has no floating-point circuitry at all can obtain a FLOPS rating if it properly carries out the Linpack benchmark.

High-speed floating-point calculations certainly aren’t important to every computer user. Recognizing this, Reinhold P. Weicker of Siemens Nixdorf Information Systems wrote a benchmarking program in 1984 that focused on string manipulation and integer operations. He called his program the Dhrystone benchmark, reportedly as a pun on the Whetstone benchmark. The program is CPU bound, performing no I/O or system calls. Unlike WIPS, Dhrystone results are reported simply as Dhrystones per second (the number of times the test program can be run in one second), not in DIPS or Mega-DIPS!

With respect to their algorithms and their reported results, the Whetstone, Linpack, and Dhrystone benchmarks have the advantage of being simple and easy to understand. Unfortunately, that is also their major limitation. Because the operations of these programs are so clearly defined, it is easy for compiler writers to equip their products with “Whetstone,” “Linpack,” or “Dhrystone” compilation switches. When set, these compiler options invoke special code that is optimized for the benchmarks. Furthermore, the compiled objects are so small that the largest portion of the program stays in the cache of today’s systems. This just about eliminates any chance of assessing a system’s memory management capabilities.

Designing compilers and systems so that they perform optimally when running benchmarking programs is a practice that is as old as the synthetic benchmarks themselves. So long as there is economic advantage in being able to report good numbers, manufacturers will do whatever they can to make their numbers look good. When their numbers are better than those of their competition, they waste no time in advertising their “superior” systems. This widespread practice has become known as benchmarketing. Of course, no matter how good the numbers are, the only thing that benchmark results really tell you is how well the tested system runs the benchmark, and not necessarily how well it will run anything else-especially your particular workload.

10.4.3 Standard Performance Evaluation Corporation Benchmarks

The science of computer performance measurement benefited greatly by the contributions of the Whetstone, Linpack, and Dhrystone benchmarks. For one thing, these programs gave merit to the idea of having a common standard by which all systems could be compared. More importantly, although unintentionally, they demonstrated how easy it is for manufacturers to optimize their products’ performance when a contrived benchmark is small and simple. The obvious response to this problem is to devise a more complex benchmark that also produces easily understood results. This is the aim of the SPEC CPU benchmarks.

SPEC (Standard Performance Evaluation Corporation) was founded in 1988 by a consortium of computer manufacturers in cooperation with the Electrical Engineering Times. SPEC’s main objective is to establish equitable and realistic methods for computer performance measurement. Today, this group encompasses over 60 member companies and three constituent committees. These committees are the:

• Open Systems Group (OSG), which addresses workstation, file server, and desktop computing environments.

• High-Performance Group (HPG), which focuses on enterprise-level multiprocessor systems and supercomputers.

• Graphics Performance Characterization Group (GPC), which concentrates on multimedia and graphics-intensive systems.

These groups work with computer users to identify applications that represent typical workloads, or those applications that can distinguish a superior system from the rest. When I/O routines and other non-CPU-intensive code are pared away from these applications, the resulting program is called a kernel. A SPEC committee carefully selects kernel programs from submissions by various application communities. The final collection of kernel programs is called a benchmark suite.

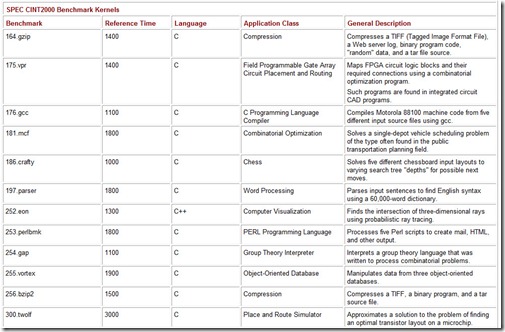
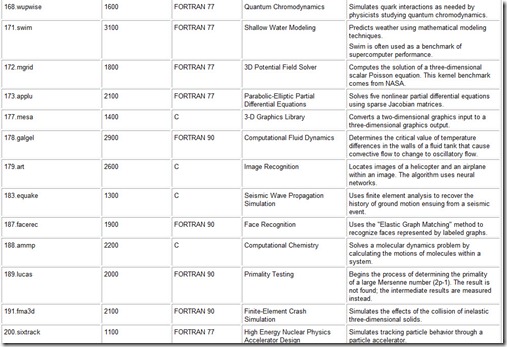
The most widely known (and respected) of SPEC’s benchmarks is its CPU suite, which measures CPU throughput, cache and memory access speed, and compiler efficiency. The latest version of this benchmark is CPU2000, with CPU2004 currently under development. CPU2000 consists of two parts: CINT2000, which measures how well a system performs integer processing, and CFP2000, which measures floating-point performance (see Table 10.7). (The “C” in CINT and CFP stands for “component.” This designation underscores the fact that the benchmark tests only one component of the system.)

Table 10.7: The Constituent Kernels of the SPEC CPU2000 Benchmark Suite

CINT2000 consists of 12 applications, 11 of which are written in C and one in C++. The CFP2000 suite consists of 14 applications, 6 of which are written in FORTRAN 77, 4 in FORTRAN 90, and 4 in C. The results (system throughput) obtained by running these programs are reported as a ratio of the time it takes the system under test to run the kernel to the time it takes a reference machine to run the same kernel. For CPU2000, the reference machine is a Sun Ultra 10 with a 300MHz CPU. A system under test will almost certainly be faster than the Sun Ultra 10, so you can expect to see large positive numbers cited by vendors. The larger, the better. A complete run of the entire SPEC CPU2000 suite requires just over two 24-hour days to complete on most systems. The reported CINT2000 and CFP2000 result is a geometric mean of the ratios for all component kernels. (See the sidebar “Calculating the SPEC CPU Benchmark” for details.)

With system sales so heavily dependent on favorable benchmark results, one would expect that computer manufacturers would do everything within their power to find ways of circumventing SPEC’s rules for running the benchmark programs. The first trick was the use of compiler “benchmark switches,” as had become traditional with the Whetstone, Linpack, and Dhrystone programs. However, finding the perfect set of compiler options to use with the SPEC suite wasn’t quite as simple as it was with the earlier synthetic benchmarks. Different settings are often necessary to optimize each kernel in the suite, and finding the settings is a time-consuming and tedious chore.

SPEC became aware of the use of “benchmark special” compiler options prior to the release of its CPU95 benchmark suite. It attempted to put an end to the benchmark specials by mandating that all programs in the suite written in the same language must be compiled using the same set of compiler flags. This stance evoked immediate criticism from the vendor community, arguing that their customers were entitled to know the best possible performance attainable from a system. Furthermore, if a customer’s application were similar to one of the kernel programs, the customer would have much to gain by knowing the optimal compiler options.

These arguments were sufficiently compelling for SPEC to allow the use of different compiler flags for each program in a suite. In the interest of fairness to all, however, manufacturers report two sets of results for SPEC CPU2000. One set is for tests where all compiler settings are the same for the entire suite (the base metric), and the second set gives results obtained through optimized settings (the peak metric). Both numbers are reported in the benchmark compilations, along with complete disclosure of the compiler settings for each run.

Users of the SPEC benchmarks pay an administrative fee for the suite’s source code and instructions for its installation and compilation. Manufacturers are encouraged (but not required) to submit a report that includes the results of the benchmarks to SPEC for review. After SPEC is satisfied that the tests were run in accordance with its guidelines, it publishes the benchmark results and configuration disclosure reports on its Web site. SPEC’s oversight assures that the manufacturer has used the benchmark software correctly and that the system’s configuration is completely revealed.

Although processor wars generate reams of coverage in the computer trade press, Amdahl’s law tells us that a useful system requires more than simply a fast CPU. Computer buyers are interested in how well an entire system will perform under their particular workloads. Toward this end, SPEC has created an array of other metrics, including SPEC Web for Web servers, SPEC HPC for high-performance computers, and SPEC JVM for client-side Java performance. SPEC JVM is complemented by SPEC JBB (Java Business Benchmark) for Java server performance. Each of these benchmarks adheres to SPEC’s philosophy of establishing fair and objective system performance measurements.

10.4.4 Transaction Performance Council Benchmarks

SPEC’s benchmarks are helpful to computer buyers whose principal concern is CPU performance. They are not quite so beneficial to buyers of enterprise transaction-processing servers. For systems in this class, buyers are most interested in the server’s ability to process a great number of concurrent short-duration activities, where each transaction involves communications and disk I/O to some extent.

Sluggish transaction-processing systems can be enormously costly to businesses, causing far-reaching problems. When a customer-service system is slow, long lines of grumpy customers are detrimental to a retail store’s image. Customers standing in slow-moving lines at checkout counters don’t care that a credit authorization system is bogging things down. Lethargic automated teller machines and unresponsive point-of-sale debit systems can alienate customers in droves if their wait is too long. Transaction-processing systems aren’t merely important to the customer service sector; they are its lifeblood. Wise business leaders are willing to invest small fortunes to keep their customers satisfied. With so much at stake, it is essential to find some method of objectively evaluating the overall performance of systems supporting these critical business processes.

Computer manufacturers have always had ways of gauging the performance of their own systems. These measurements are not intended for public consumption, but are instead for internal use by engineers seeking ways to make their systems (or parts of them) perform better. In the early 1980s, the IBM Corporation invented such a benchmark to help with the design of its mainframe systems. This benchmark, which they called TP1 (TP for transaction processing), eventually found its way into the public domain. A number of competing vendors began using it and announcing their (amazing) results. Transaction processing experts were critical of this practice because the benchmark wasn’t designed to simulate a real transaction processing environment. For one thing, it ignored network delays and the variability of user “think time.” Stated another way, all that TP1 could do was measure peak throughput under ideal conditions. Although this measurement was useful to system designers, it didn’t give the computer buyer much to go on.

Calculating The SPEC CPU Benchmark

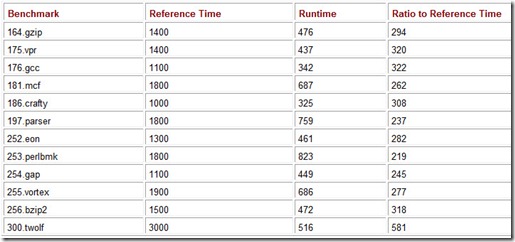
As we stated in the text, the first step in calculating SPEC benchmark results is to normalize the time it takes for a reference machine to run a benchmark kernel to the time it takes for the system under test to run the same kernel program. This is a simple ratio, which is then multiplied by 100. For example, suppose a hypothetical system runs the 164.gzip kernel in 476 seconds. The reference machine took 1400 seconds to run the same program. The normalized ratio is: 1400 ÷ 476 x 100 = 294 (rounded to a whole number). The final SPECint result is the geometric mean of all of the normalized ratios in the integer program suite. Consider the results shown in Table 10.8.

294 x 320 x 322 x 262 x 308 x 237 x 282 x 219 x 245 x 277 x 318 x 581 » 4.48 x 10²⁹

Table 10.8: A Set of Hypothetical SPECint Results

To determine the geometric mean, first find the product of all 12 normalized benchmark times:

Then take the twelfth root of this product:

Thus, the CINT metric for this system is (a fairly impressive) 296. If this result were obtained when running benchmarks compiled with standard (conservative) compiler settings, it would be reported as the “base” metric, SPECint_base_2000. Otherwise, it is the SPECint2000 rating for this system.

The CINT2000 and CFP2000 suites measure a CPU’s capabilities when running only one image of each benchmark at a time. This single-thread model doesn’t tell us anything about how well the system handles concurrent processes. SPEC CPU “rate” metrics give us some insight here. Calculation of SPECint_rate metrics is a bit more complicated than calculating single-thread SPECint metrics.

To find a rate metric, a number of identical benchmark kernel processes are started in the host. For the sake of example, let’s say we start four concurrent 164.gzip processes. After all instances of the 164.gzip program terminate, we find the elapsed time by subtracting the time that the last instance finishes from the time that the first one started. Suppose our time difference is 450 seconds. We divide this figure into 3600 seconds to give a “number of runs per hour” rate, which is:

Next, the largest reference time in the suite, which is the 171.swim benchmark of the floating-point suite, is normalized to the reference time of the benchmark. For 164.gzip the normalization figure is approximately:

The product of these two figures with the number of copies run yields the SPECint_rate2000 metric for this benchmark. Because we are running four copies of the benchmark, we have (rounded to one decimal place):

4 x 8 x 0.45161 = 14.5.

The SPECint_rate2000 metric that will be reported for this system is the geometric mean of all of the component CINT2000 kernels. The same process is used in determining the SPECfp_rate results.

In 1985, Jim Gray, one of the more vocal critics of TP1, worked with a large group of his fellow dissenters to propose a benchmark that would address the shortcomings of TP1. They called their benchmark DebitCredit to emphasize its focus on business transaction processing performance. In addition to specifying how this benchmark would work, Gray and his group proposed that the outcome of the system tests should be reported along with the total cost of the system configuration that was tested. They offered ways in which the benchmark could be scaled proportionately to make the tests fair across various sizes of systems.

DebitCredit was welcomed by the vendor community because it delivered a clear and objective performance measurement. Before long, most vendors were using it, announcing their good results with reckless abandon. Unfortunately, no formal mechanism was in place to verify or refute their claims. In essence, manufacturers could cite whatever results they thought would give them an advantage over their competition. Clearly, some means of independent review and control was desperately needed. To this end, in 1988, Omri Serlin persuaded eight computer manufacturers to join together to form the independent Transaction Processing Council (TPC). Today, the TPC consists of approximately 40 companies, including makers of system software as well as hardware.

The first task before the TPC was to release a benchmark suite bearing its official stamp. This benchmark, released in 1990, was called TPC-A. In keeping with the pace of technological innovation, as well as the advances of benchmarking science, TPC-A is now in the fifth version of its third major revision, TPC-C Version 5.

The TPC-C benchmarking suite models the activities of a wholesale product distribution company. The suite is a controlled mix of five transaction types that are typical of order fulfillment systems. These transactions include new order initiation, stock level inquiries, order status inquiries, goods delivery postings, and payment processing. The most resource-intensive of these transactions is the order initiation transaction, which must constitute at least 45% of the transaction mix.

TPC-C employs remote terminal emulation software that simulates a user’s interaction with the system. Each interaction takes place through a formatted data entry screen that would be usable by a human data entry clerk. The emulator program picks its transactions from a menu, just as a real person would do. The choices, however, are statistically randomized so that the correct transaction mix is executed. Input values, such as customer names and part numbers, are also randomized to avoid repeated cache hits on the data values, thus forcing frequent disk I/O.

TPC-C’s end-to-end response time is measured from the instant that the “user” has completed the required entries to the instant the system presents the required response at the terminal. Under the latest TPC-C rules, 90% of all transactions, except the stock level inquiry, must be accurately completed within five seconds. The stock inquiry is excepted from the five-second rule because stock levels may be checked in a number of different warehouses within a single inquiry transaction. This task is more I/O intensive than the others.

Keeping in mind that the TPC-C suite simulates a real business that uses a real system, every update transaction must support the ACID properties of a production database. (These properties are described in Chapter 8.) TPC-C’s ACID properties include record locking and unlocking, as well as the rollback capability provided by logging updates to a database journal file.

The TPC-C metric is the number of new order transactions completed per minute (tpmC), while a mix of the other transactions is concurrently executing on the same system. Reported TPC-C results also include a price-performance ratio, which is found by dividing the cost of the system by the throughput metric. Hence, if a $90,000 system provides a throughput of 15,000 tpmC, its price-performance ratio is $6 per tpmC. The system cost includes all hardware, software, and network components that are required to execute the TPC-C transactions. Each component used in the test must be available for sale to the general public at the time the results are reported. This rule is intended to prevent the use of benchmark special components. All of the system components involved in producing the reported benchmark results must be listed (in great detail) on a full-disclosure report submitted to the TPC. The disclosed configuration must also include all tuning parameters ^[1](e.g., compiler switches) in effect during the test. The full-disclosure report also includes “total cost of ownership” figures that take into account the cost of three years of maintenance and support for the entire system.

When a vendor submits its TPC-C results to the TPC, all of the information in the reports is audited by an independent auditing firm to assure its completeness and accuracy. (Of course, the auditor cannot rerun the test, so the throughput figures are usually taken at face value if the test was performed correctly.) Once the reports are accepted by the TPC, they are published on the Web for inspection by customers and competitors alike. On occasion, a competitor or the TPC itself challenges a manufacturer’s results. In these situations, the manufacturer may either withdraw or defend its report. Sometimes the report is quietly withdrawn because the cost of defending the results is prohibitive, even if a manufacturer is well founded in its claims. A vendor may also choose to withdraw its results because the tested configuration is no longer available or the next model of the system is greatly improved over the old one.

TPC-C is just one of several benchmarks sponsored by the Transaction Processing Council. When the TPC was founded, the world of business computation consisted primarily of transaction processing systems that also supported financial processes such as bookkeeping and payroll. These systems took a clearly defined set of inputs and produced a clearly defined output, usually in the form of printed reports and forms. This deterministic model lacks the flexibility needed to provide deep data analysis tools required in today’s business environment. Many companies have replaced their static reports with decision support tools. These applications access enormous quantities of input data to produce business intelligence information for marketing guidance and business logistics. In a sense, decision support applications are the complete opposite of transaction processing applications. They require a different breed of computer system. Whereas transaction processing environments handle large numbers of short-duration processes, decision support systems handle a small number of long-duration processes.

TPC Benchmarks – A Reality Check

The Transaction Performance Council has made every attempt to model realworld scenarios with its TPC-C, TPC-H, and TPC-R benchmarks. It has taken great pains to ensure that the benchmarks contain a realistic mix of common business transactions and activities. These activities are randomized to generate as much I/O activity as possible. Specifically, data should be fetched most often directly from disk rather than from cache or other fast memory.

The thinking behind this is that the tests shouldn’t be biased toward one particular type of architecture. If the data weren’t randomized, the benchmark would favor systems with large cache memories that may not perform (proportionately) as well in real environments.

For many years, this idea was unchallenged until a doctoral student intern at IBM, Windsor W. Hsu, conducted a series of empirical studies. Under the auspices of IBM’s Almaden Research Center, Hsu and his fellow researchers monitored millions of transactions on systems owned by ten of IBM’s largest customers. Hsu’s work validated many aspects of the TPC benchmarks, including their workload mix. However, Hsu found that real-world activity differed from the TPC models in two important ways.

First, the TPC benchmarks exhibit a sustained and constant transaction rate. This is what they are designed to do in order to fully stress a system at peak workload rates. But Hsu found that real workloads are bursty. A flurry of activity occurs, and then there is a lull before the next flurry of activity occurs. What this means to designers is that overall performance could be improved if effective dynamic resource allocation facilities were incorporated into the system software and hardware. Although many vendors do in fact use dynamic resource allocation, their efforts are not rewarded in the TPC benchmarks.

Hsu’s second major result challenges the notion of randomizing the data and the workload in the TPC benchmarks. He found that real systems exhibit significantly greater “pseudo-sequentiality” than the TPC programs do. This finding is important because many systems prefetch data from disk and memory. Real workloads benefit greatly when prefetching is used. Furthermore, the pseudo-sequentiality of data access patterns lends itself well to least recently used (LRU) cache and memory page replacement policies. The TPC benchmarks do not.

Hsu’s work is not an indictment against the TPC benchmarks. Instead, it amplifies the folly of thinking that one can extrapolate benchmark results into particular real-world situations. Although the TPC benchmarks don’t model the real world as well as some would like, they continue to be an honest and fairly reliable yardstick to use when comparing performance among different systems’ architectures.

No one can reasonably expect decision support systems to produce the instantaneous results characteristic of a simple online order status inquiry. However, there are limits to the amount of time one is willing to wait, no matter how useful the end result will be. In fact, if a decision support system is “too slow,” executives will be reluctant to use it, thus defeating its purpose. So even in the cases where we are willing to wait “a while” for our answers, performance remains an issue.

In response to this relatively new area of computing, the TPC produced two benchmarks, TPC-H and TPC-R, to describe the performance of decision support systems. Although both of these benchmarks are directed at decision support systems, the TPC-R benchmark measures performance when the reporting parameters of the system are known in advance (the database can be indexed and optimized for the reporting). The TPC-H benchmark measures how well a system can produce ad hoc query results, which are queries where the parameters of the query are not known in advance. Results of TPC-H tests are given in queries per hour, QphH, and those of TPC-R as QphR. The TPC categorizes these results according to the size of the databases against which the queries were run, because running a query against 100 gigabytes of data is a far different task than running a query against a terabyte of data.

In keeping with the times, the TPC also has defined a benchmark for measuring Web server performance, TPC-W. The operation of this suite is philosophically similar to that of the TPC-C benchmark. Randomized transactions are entered through a “remote browser emulator” accessing a set of options presented to a customer. The customer selections are typical of those usually found on a retail e-commerce site: browsing through a catalog of items, viewing a shopping cart, and executing purchase of the items in the shopping cart using a secure connection. The TPC-W metric is Web interactions per second,or WIPS^[2]. TPC-W uses two mixtures of option selection patterns. Both were empirically determined through analysis of logs gathered from real e-commerce sites. One mix of option selections, WIPSb, is geared toward Web sites where visitors do more browsing than buying; the other, WIPSo, is for Web sites where customers do more buying (or ordering) than browsing. As with TPC-C, TPCW transactions must maintain the ACID properties of correct database transactions.

TPC-H, TPC-R, and TPC-W results are subject to the same strict auditing controls as TPC-C. Thus, these metrics are trustworthy aids in selecting systems to serve the computing needs of the enterprise. The principal pitfall in the use of TPC benchmarks is assuming that the benchmarks accurately predict the performance of a system under anyone’s particular workload. This is not TPC’s claim or intent. Research has shown the ways in which one particular set of real workloads differs from the TPC workloads (see sidebar). Computer benchmarks, when used correctly, are indispensable tools. Used incorrectly, they can lead us down paths where we would rather not venture.

10.4.5 System Simulation

The TPC benchmarks differ from the SPEC benchmarks in that they endeavor to simulate a complete computing environment. Although the purpose of the TPC benchmarks is to measure performance, their simulated environment may also be useful to predict, and hence optimize, performance under various conditions. In general, simulations give us tools that we can use to model and predict aspects of system behavior without the use of the exact live environment that the simulator is modeling.

Simulation is very useful for estimating the performance of systems or system configurations that do not yet exist. Prudent system designers always conduct simulation studies of new hardware and software prior to building commercial versions of their products. The wisdom of this approach was shown dramatically in 1967 by Stanford doctoral candidate Norman R. Nielson in his thesis “The Analysis of General Purpose Computer Time-Sharing Systems.” Nielson’s thesis documented his simulation study of IBM’s yet-to-be-released 360/67 Time-Sharing System (TSS). Using IBM’s published specifications, Nielson’s work revealed serious flaws in the 360/67 TSS. His findings impelled IBM to improve upon the system’s design prior to its widespread release.

Simulations are models of particular aspects of full systems. They give system designers the luxury of performing “what if” testing in a controlled environment separate from the live system. Suppose, for example, that you are interested in maximizing the number of concurrent tasks that a system can sustain. The tuning parameters include the memory allocation for each task and its CPU timeslice duration. Based on what you know about the characteristics of each task, the tuning values could be adjusted until an optimal balance is found. Such tinkering in a live environment having real tasks and real users incurs some real risks, the worst of which might be that no one gets any work done.

One of the major challenges of system simulation lies in determining the characteristics of the workload. The workload mix should correspond to the system components that are modeled. One approach starts by examining system logs to derive a synthetic, yet statistically sound, workload profile. This is the method used by the TPC in producing the workload mix for its TPC-W benchmark.

Capturing the behavior of an entire system or its entire workload will not produce sufficient data granularity if a simulator is focused on only one component of the system. Say, for example, a system designer is trying to determine an ideal set-associative memory cache configuration. This configuration includes the sizes of the level 1 and level 2 caches, as well as the set size for each cache block. For this type of simulation, the simulator needs detailed memory access data. This kind of information is usually derived from system traces.

System traces gather detailed behavior information using hardware or software probes into the activity of the component of interest. Probes trace every detail of the component’s actual behavior, possibly including binary instructions and memory references. Traces gathered by probes consist of only a few seconds of system activity because the data set output is very large. In producing a statistically meaningful model, several traces are required.

When designing a simulator, a clear definition of the purpose of the simulator must be established. Good engineering judgment is required to separate the important from the unimportant system characteristics. A model that is too detailed is costly and time-consuming to write. Conversely, simulators that are so simplistic that they ignore key factors produce misleading results. System simulation is an excellent tool, but like any tool, we must have some assurance of its suitability for the job. System simulators must be validated to affirm the assumptions around which the model was built. The simplest models are the easiest to validate.

10.5 CPU PERFORMANCE OPTIMIZATION

CPU performance has long been the principal focus of system optimization efforts. There is no single way to enhance CPU performance, because CPU throughput is affected by a multitude of factors. For instance, program code affects the instruction count; the compiler influences both the instruction count and the average clock cycles per instruction; the ISA determines the instruction count and the average clock cycles per instruction; and the actual hardware organization establishes the clock cycles per instruction and the clock cycle time.

Potential CPU optimization techniques include integrated floating point units, parallel execution units, specialized instructions, instruction pipelining, branch prediction, and code optimization. Because all but the last two items have been addressed in previous chapters, we focus our attention on branch prediction and user code optimization.

10.5.1 Branch Optimization

At this point, you should be very familiar with the fetch-decode-execute cycle. Instruction pipelining has a significant influence on performance and is incorporated in most contemporary architectures. However, branching imposes a penalty on this pipeline. Consider a conditional branching situation in which the address of the next instruction is not known until the current instruction execution is complete. This forces a delay in the flow of instructions through the pipeline because the processor does not know which instruction comes next until it has finished executing the branch instruction. In fact, the longer the pipeline is (the more stages it has), the more time the pipeline must wait before it knows which instruction to feed next into the pipeline.

Modern processors have increasingly longer pipelines. Typically, 20% to 30% of machine instructions involve branching, and studies indicate that approximately 65% of the branches are taken. Additionally, programs average about five instructions between branches, forcing many pipeline stalls, thus creating a growing need to reduce the penalties imposed by branching. The factors contributing to pipeline stalls are called hazards. They include such things as data dependencies, resource conflicts, and fetch access delays from memory. Aside from stopping the pipeline upon detection of a hazard, there is little that can be done about them. Branch optimization, however, is within the scope of our control. For this reason, branch prediction has been the focus of recent efforts toward improving CPU performance.

Delayed branching is one method of dealing with the effects branching has on pipelines. When performing a conditional branch, for example, one or more instructions after the branch are executed regardless of the outcome of the branching. The idea is to utilize otherwise wasted cycles following a branch. This is accomplished by inserting an instruction behind the branch and then executing it before the branch. The net effect is that the instruction following the branch is executed before the branch takes effect.

This concept is best explained by way of an example. Consider the following program:

      Add R1, R2, R3
      Branch Loop
      Div R4, R5, RR6
Loop: Mult ...

This results in the following trace for the pipeline:

The divide instruction represents a wasted instruction slot, because the instruction is fetched but never decoded or executed due to the branch. This slot could be filled with another instruction by reversing the execution sequence of the branch instruction and another instruction that will be executed anyway:

It should be clear that delayed branching, although it uses otherwise wasted branch delay slots, actually reorders the execution sequence of the instructions. The compiler must, therefore, perform a data dependency analysis to determine whether delayed branching is possible. Situations may arise in which no instruction can be moved after the branch (into the delay slot). In this case, a NOP (“no operation” instruction that does nothing) is placed after the branch. Clearly, the penalty for branching in this case is the same as if delayed branching were not employed.

A compiler can choose the instruction to place in the delay slot in a number of ways. The first choice is a useful instruction that executes regardless of whether the branch occurs. The instructions before the branch statement are the prime candidates. Other possibilities include instructions that execute if the branch occurs but do no harm if the branch does not occur. The reverse of this is also considered: statements that execute if the branch does not occur but do no harm if the branch does occur. Candidates also include those statements that do no harm regardless of whether the branch occurs. Delayed branching has the advantage of low hardware cost, and is very dependent on the compiler to fill the delay slots.

Another approach to minimizing the penalty introduced with branching is branch prediction. Branch prediction is the process of attempting to guess the next instruction in the instruction stream, thus avoiding pipeline stalls due to branching. If the prediction is successful, no delay is introduced into the pipeline. If the prediction is unsuccessful, the pipeline must be flushed and all calculations caused by this miscalculation must be discarded. Branch prediction techniques vary depending on the branch characterization: loop control branching, if/then/else branching, or subroutine branching.

To take full advantage of branch prediction, the pipeline must be kept full. Therefore, once a prediction is made, the instruction is fetched and execution begins. This is called speculative execution. These instructions are executed before it is known for sure whether they will need to execute. This work must be undone if a prediction is found to be incorrect.

Branch prediction is like a black box into which we feed various input data, getting a predicted target instruction as output. When the code in question is simply fed into this black box, this is known as static prediction. If, in addition to the code, we feed in state history (previous information about the branch instruction and its outcomes in the past), the black box is using dynamic prediction. Fixed predictions are those that are always the same: Either the branch will be taken or it will not, and every time the branch is encountered, the prediction is the same. True predictions have two potential outcomes, either “take branch” or “do not take branch.”

In fixed prediction, when the assumption is that the branch is not taken, the idea is to assume that the branch will not occur and continue on the normal sequential path. However, processing is done in parallel in case the branch occurs. If the prediction is correct, the preprocessing information is deleted and execution continues. If the prediction is incorrect, the speculative processing is deleted and the preprocessing information is used to continue on the correct path.

In fixed prediction, when the assumption is that the branch is always taken, preparation is also made for an incorrect prediction. State information is saved before the speculative processing begins. If the guess is correct, this saved information is deleted. If the prediction is incorrect, the speculative processing is deleted and the information is used to restore the execution environment, at which time the proper path is taken.

Dynamic prediction increases the accuracy of branch prediction by using a recorded history of previous branches. This information is then combined with the code and fed into the branch predictor (our black box). The principal component used for branch prediction is a branch prediction buffer. This high-speed buffer is indexed by the lower portion of the address of the branch instruction, with additional bits indicating whether the branch was recently taken. Branch prediction buffers always return a prediction using a small number of bits. One-bit dynamic prediction uses a single bit to record whether the last occurrence of the branch was taken. Twobit prediction retains the history of the two previous branches for a given branch instruction. The extra bit helps reduce mispredictions at the end of loops (when the loop exits instead of branching as before). The two branch prediction bits can represent state information in various ways. For example, the four possible bit patterns can indicate the historical probability of taking the branch (11: strongly taken; 10: weakly taken; 01: weakly not taken; and 00: strongly not taken). The probabilities are changed only if a misprediction occurs twice.

Early implementations of branch prediction were almost exclusively of the static variety. Most newer processors (including the Pentium, PowerPC, UltraSparc, and Motorola 68060) use 2-bit dynamic branch prediction, which has resulted in higher accuracy and fewer mispredictions. Some superscalar processors mandate its use, whereas others offer it as an option. A number of systems offload branch prediction processing to specialized circuits, which produce more timely and accurate predictions.

10.5.2 Use of Good Algorithms and Simple Code

The world’s best processor hardware and optimizing compilers can go only so far in making programs faster. They will never be equal to a human who has mastered the science of effective algorithm and coding design. Recall from Chapter 6 the example of accessing an array row major versus column major. The basic idea was that matching the access of the data more closely to how it is stored can increase performance. If an array is stored row major, and you access it in column-major order, the principle of locality is weakened, potentially resulting in degraded performance. Although compilers can improve performance to some extent, their scope is primarily limited to low-level code optimization. Program code can have a monumental impact on all aspects of performance, from pipelining to memory to I/O. This section is devoted to those mechanisms that you, as a programmer, can employ to achieve optimal performance from your computer.

Operation counting is one way to enhance the performance of your program. With this method, you estimate the number of instruction types that are executed in a loop, then determine the number of machine cycles required for each instruction type. This information can then be used to achieve a better instruction balance. The idea is to attempt to write your loops with the best mix of instructions for a given architecture (e.g., loads, stores, integer operations, floating-point operations, system calls). Keep in mind that a good instruction mix for one hardware platform may not be a good mix for a different platform.

Loops are used extensively in programs and are excellent candidates for optimization. In particular, nested loops present a number of interesting optimization opportunities. With some investigation, you can improve memory access patterns and increase instruction level parallelism. Loop unrolling is one approach easily employed by any programmer. Loop unrolling is the process of expanding a loop so that each new iteration contains several of the original iterations, thus performing more computations per loop iteration. In this way, several loop iterations are processed each time through the loop. For example:

for (i = 1; i <= 30; i++)
    a[i] = a[i] + b[i] * c;

When unrolled (twice) becomes:

for (i = 1; i <= 30; i+=3)
    { a[i] = a[i] + b[i] * c;
       a[i+1] = a[i+1] + b[i+1] * c;
        a[i+2] = a[i+2] + b[i+2] * c; }

Upon first inspection, this appears to be a bad way to write code. But it reduces loop overhead (such as the maintenance of the index variable) and helps with control hazards in pipelines. It typically enables operations from different loop iterations to execute in parallel. In addition, it allows for better instruction scheduling due to less data dependence and better register usage. Clearly the amount of code is increased, so this is not a technique that should be employed for every loop in your program. It is best used in sections of code that account for a significant portion of the execution time. Optimization efforts give the greatest reward when applied to those parts of the program that will yield the greatest improvement. This technique is also suitable for while loops, although its application is not so straightforward.

Another useful loop optimization technique is loop fusion. Loop fusion combines loops that use the same data items. This can result in increased cache performance, increased instruction level parallelism, and reduced loop overhead. Loop fusion on the following loops:

for (i=0; i<N; i++)
    C[i] = A[i] + B[i];
for (i=0; i<N; i++)
    D[i] = E[i] + C[i];

results in:

for (i=0; i<N; i++) {
    C[i] = A[i] + B[i];
    D[i] = E[i] + C[i];}

Program Optimization Tips

• Give the compiler as much information as possible about what you are doing. Use constants and local variables where possible. If your language permits them, define prototypes and declare static functions. Use arrays instead of pointers when you can.

• Avoid unnecessary type casting and minimize floating-point to integer conversions.

• Avoid overflow and underflow.

• Use a suitable data type (e.g., float, double, int ).

• Consider using multiplication instead of division.

• Eliminate all unnecessary branches.

• Use iteration instead of recursion when possible.

• Build conditional statements (e.g., if, switch, case ) with the most probable cases first.

• Declare variables in a structure in order of size with the largest ones first.

• When a program is having performance problems, profile the program before beginning optimization procedures. (Profiling is the process of breaking your code into small chunks and timing each of these chucks to determine which of them take the most time.)

• Never discard an algorithm based solely on its original performance. A fair comparison can occur only when all algorithms are fully optimized.

Sometimes, the potential for loop fusion is not as obvious as it is in the above code. Given the code segment:

for (i=1; i<100; i++)
    A[i] = B[i] + 8;
for (i=1; i<99; i++)
    C[i] = A[i+1] * 4;

It isn’t clear how to fuse these loops because the second one uses a value from array A that is one ahead of the loop counter. However, we could easily rewrite this code as:

A[1] = B[1] + 8;
for (i=2; i<100; i++) {
    A[i] = B[i] + 8;}
for (i=1; i<99; i++) {
    C[i] = A[i+1] * 4; }

Now we are ready to fuse the loops:

i = 1;
A[i] = B[i] + 8;
for (j=0; j<98; j++) {
    i = j + 2;
    A[i] = B[i] + 8;
    i = j + 1;
    C[i] = A[i+1] * 4; }

Loop fission, splitting large loops into smaller ones, also has a place in loop optimization, because it can eliminate data dependencies and reduce cache

delays resulting from conflicts. One example of loop fission is loop peeling, the process of removing the beginning or ending statements from a loop. These are the statements that usually contain the loop’s boundary conditions. For example, the code:

for (i=1; i<N+1; i++) {
   if (i==1)
     A[i] = 0;
   else if (i==N)
     A[i] = N;
   else
     A[i] = A[i] + 8;}

Becomes:

A[1] = 0;
for (i=2; i<N; i++){
    A[i] = A[i] + 8; }
A[N] = N;

This example of loop peeling results in more instruction level parallelism because it removes branching from the loop.

We have already alluded to loop interchange, which is the process of rearranging loops so that memory is accessed more closely to the way in which the data is stored. In most languages, loops are stored in row-major order. Accessing data in row-major versus column-major order results in fewer cache misses and better locality of reference.

Loop optimization is an important tool for improving program performance. It exemplifies how you can use your knowledge of computer organization and architecture to write superior programs. We have provided a sidebar containing a list of things to keep in mind while you are optimizing your program code. We invite you to ponder the ways in which each of these tips takes various system components into account. You should be able to explain the rationale behind each of them.

The more things you try, the more successful you will be. Keep in mind that often a tweak that should result in increased performance isn’t immediately successful. Many times, these ideas must be used in combination for their effects to be apparent.

^[1] Tuning information supplied in full-disclosure reports is a valuable resource for system administrators seeking to optimize the performance of a system similar to one covered by a TPC-C report. Because a real workload is not identical to the TPC-C suite, the reported tuning information may not give optimal results, but it’s often a good starting point.

^[2] These WIPS are not to be confused with Whetstone Instructions per Second. Are we already running out of unique four-letter acronyms?

10.6 Disk Performance

Although CPU and memory performance are important factors in system performance, optimal disk performance is crucial to system throughput. The vast majority of user interactions with a system involve some kind of disk input or output. Furthermore, this disk I/O can happen through a page fault, its timing and duration being beyond the control of either the user or the programmer. With a properly functioning I/O subsystem, total system throughput can be an order of magnitude better than when the I/O subsystem is functioning poorly. Because the performance stakes are so high, disk systems must be well designed and well configured from the outset. Throughout the life of the system, disk subsystems must be continually monitored and tuned. In this section, we introduce the principal aspects of I/O system performance. The generic concepts introduced here will be useful to you whether you are selecting a new system or trying to keep an existing system running at its best.

10.6.1 Understanding the Problem

Disk drive performance issues loom large in overall system performance because retrieving an item from a disk takes such a long time, relative to CPU or memory speed. A CPU needs only a few nanoseconds to execute an instruction when all operands are in its registers. When the CPU needs an operand from memory before it can complete a task, the execution time may rise to tens of nanoseconds. But when the operand must be fetched from the disk, the time required to complete the task soars to tens of milliseconds—a million-fold increase! Moreover, because the CPU can dispatch I/O requests much faster than disk drives can keep up with them, disk drives can become throughput bottlenecks. In fact, when a system exhibits “low” CPU utilization, it can be because the CPU is continually waiting for I/O requests to complete. Such a system is I/O bound.

One of the most important metrics of I/O performance is disk utilization, the measure of the percentage of time that the disk is busy servicing I/O requests. Stated another way, disk utilization gives the probability that the disk is busy when another I/O request arrives in the disk service queue. Utilization is determined by the speed of the disk and the rate at which requests arrive in the service queue. Stated mathematically:

where the arrival rate is given in requests per second, and the disk service rate is given in I/O operations per second (IOPS).

For example, consider a particular disk drive that can complete an I/O operation in 15ms. This means that its service rate is about 67 I/O operations per second (0.015 seconds per operation = 66.7 operations per second). If this disk gets 33 I/O requests per second, it is about 50% utilized. Fifty-percent utilization gives good performance on practically any system. But what happens if this system starts seeing a sustained I/O request rate of 60 requests per second? Or 64 requests per second? We can model the effects of the increasing load using a result from queuing theory. Simply stated, the amount of time that a request spends in the queue is directly related to the service time and the probability that the disk is busy, and it is indirectly related to the probability that the disk is idle. In formula form, we have:

By substitution, it is easy to see that when the I/O request arrival rate is 60 requests per second, with a service time of 15ms, the utilization is 90%. Hence, a request will have to wait 135ms in the queue. This brings total service time for the request to 135 + 15 = 150ms. At 64 requests per second (only a 7% increase), completion time soars to 370ms (a 147% increase). At 65 requests per second, service time is over a half-second… from our 15ms disk drive!

The relationship between queue time and utilization (from the formula above) is shown in Figure 10.1. As you can see, the “knee” of the curve (the point at which the slope changes most drastically) is at about 78%. This is why 80% utilization is the rule-of-thumb upper limit for most disk drives.

You can readily see by our model how things could get wildly out of control. If we have a sustained request rate of 68 I/O requests per second, this disk becomes overwhelmed. And what happens if 25% of the requests generate two disk operations? These scenarios result in more complex models, but the ultimate solution to the problem lies in finding ways to keep service time at an absolute minimum. This is what disk performance optimization is all about.

10.6.2 Physical Considerations

In Chapter 7, we introduced the metrics that determine the physical performance of a disk. These metrics include rotational delay (a function of the RPM rating of the disk), seek time (the time that it takes for a disk arm to position itself over a particular disk track), and transfer rate (the rate at which the read/write head transfers data from the surface of the disk to the system bus). The sum of rotational delay and seek time represents the access time for the disk.

Lower access time and a higher transfer rate contribute to lower total service time. Service time also can be reduced by adding platters to a disk, or by adding more disks to a system. Doubling the number of disks in an I/O system typically increases throughput by 50%. Replacing existing disks with the same number of faster disks can also result in a marked performance improvement. For example, replacing 7200 RPM disks with 10,000 RPM disks can bring a 10% to 50% performance improvement. Physical disk performance metrics are usually disclosed in specification sheets provided by manufacturers. Comparisons between brands, therefore, are usually straightforward. But as the saying goes, your mileage may vary. Performance has as much to do with how a disk is used as it does with its inherent capabilities. Raw speed has its limits.

10.6.3 Logical Considerations

Sometimes the only cure for a slow system is to add or replace disks. But this step should be taken only after all other measures have failed. In the following sections, we discuss a number of the aspects of logical disk performance. Logical considerations in disk performance are those that present us with opportunities for tuning and adjustment, tasks that should be a routine part of system operations.

Disk Scheduling

Disk arm motion is the greatest consumer of service time within most disk configurations. The average rotational delay—the time that it takes for the desired sector to move under the read/write head—is about 4ms for a 7200 RPM disk, and about 3ms for a 10,000 RPM disk (this delay is calculated as the time required for half a revolution). For this same class of disk, average seek time— the time required to position the read/write head over the desired track—ranges from 5 to 10ms. In many cases, this is twice the rotational latency of the disk. Furthermore, actual seek times can be much worse than the average. As much as 15 to 20ms can be consumed during a full-stroke seek (moving the disk arm from the innermost track to the outermost, or vice versa).

Clearly, one road to better disk performance involves finding ways to minimize disk arm motion. This can be done by optimizing the order in which requests for sectors on the disk are serviced. Disk scheduling can be a function of either the disk controller or the host operating system, but it should not be done by both, because conflicting schedules will probably result, thus reducing throughput.

The most naïve disk scheduling policy is first-come, first-served (FCFS). As its name implies, all I/O requests are serviced in the order in which they arrive in the disk service queue. The easiest way to see the problem with this approach is through an example. Let’s say we have a disk with 100 tracks, numbered 0 through 99. Processes running in the system issue requests to read tracks from the disk in the following order:

28, 35, 52, 6, 46, 62, 19, 75, 21

With the FCFS scheduling policy, assuming we are currently servicing track 40, the disk arm traces the pattern shown in Figure 10.2. As you can see by the diagram, the disk arm changes direction six times and traverses a total of 291 tracks before completing this series of requests.

Surely, arm motion could be reduced substantially if requests were ordered so that the disk arm moves only to the track nearest its current location. This is the idea employed by the shortest seek time first (SSTF) scheduling algorithm. Using the same disk track requests as listed above, assuming that the disk arm starts at track 40, the disk schedule using SSTF would be carried out as follows:

35, 28, 21, 19, 6, 46, 52, 62, 75

The pattern for this schedule is shown in Figure 10.3. As you can see, the disk arm changes direction only once and traverses a total of only 103 tracks. One shortcoming of SSTF is that starvation is possible: Theoretically, a track requested at a “remote” part of the disk could keep getting shoved to the back of the queue when requests for tracks closer to the present arm position arrive. Interestingly, this problem is at its worst with low disk utilization rates.

To avoid the starvation risk of SSTF, some fairness mechanism must be designed into the system. An easy way to do this is to have the disk arm continually sweep over the surface of the disk, stopping when it reaches a track for which it has a request in its service queue. This approach is called the elevator algorithm, because of its similarity to how skyscraper elevators service their passengers. In the context of disk scheduling, the elevator algorithm is known as SCAN (which is not an acronym). To illustrate how SCAN works, let’s say that in our example, the disk arm happens to be positioned at track 40, and is in the process of sweeping toward the inner, higher-numbered tracks. With the same series of requests as before, SCAN reads the disk tracks in the following order:

The disk arm passes over track 99 between reading tracks 75 and 35, and then travels to track zero after reading track 6, as shown in Figure 10.4. SCAN has a variant, called C-SCAN for circular SCAN, in which track zero is treated as if it is adjacent to track 99. In other words, the arm reads in one direction only, as shown in Figure 10.5. Once it passes track 99, it moves to track zero without stopping. Thus in our example, C-SCAN would read disk tracks as follows:

The disk arm motion of SCAN and C-SCAN is reduced even further through the use of the LOOK and C-LOOK algorithms. In our example, SCAN and C-SCAN continually sweep over all 100 disk tracks. But, in fact, the lowest required track is 6 and the highest is 75. Thus, if the disk arm changes direction only when the highestand lowest-numbered tracks are read, the arm will traverse only 69 tracks. This gives an arm-motion savings of about 30% over SCAN and C-SCAN.

Interestingly, at high utilization rates, SSTF performs slightly better than SCAN or LOOK. But the risk of starving an individual request persists. Under very low utilization (under 20%), the performance of any of these algorithms is acceptable.

In light of the preceding discussion of disk scheduling algorithms, a few words concerning file placement are in order. Maximum performance is realized if the most frequently used files are placed at the center of the disk. Of particular importance are the disk directory and memory page (swap) files. A central position provides the least head motion and, hence, the best access time for both SSTF and SCAN/LOOK. A worst-case situation presents itself when files are badly fragmented, that is, when a file is located in more than one contiguous disk location. If SCAN/LOOK is the scheduling method of the disk, it is possible that several full-stroke head movements will occur before the end of the file is encountered. For this reason, disks should be defragmented, or reorganized, on a regular basis. Additionally, disks should not be allowed to get too full. Another rule of thumb is that when a disk is 80% full, it is time to start removing some files. If no files can be removed, it’s time to get another disk.

Disk Caching and Prefetching

Certainly, the best way to reduce disk arm motion is to avoid using the disk to the maximum extent possible. With this goal in mind, many disk drives, or disk drive controllers, are provided with cache memory. This memory may be supplemented by a number of main memory pages set aside for the exclusive use of the I/O subsystem. Disk cache memory is usually associative. Because associative cache searches are somewhat time-consuming, performance can actually be better with smaller disk caches because hit rates are usually low.

Main memory pages dedicated to the I/O subsystem serve as a second level cache for the disk. On large servers, the number of pages set aside for this purpose is a tunable system parameter. If main memory utilization is high, the number of pages allocated to the I/O subsystem must be reduced. Otherwise, an excessive number of page faults will result, defeating the whole purpose of using main memory as an I/O cache.

Main memory I/O caches can be managed by operating system software running on the host, or they may be managed by applications that generate the I/O. Application-level cache management usually offers superior performance because it can capitalize on the characteristics particular to the application. The best applications give the user some control over the size of the cache, so that it can be adjusted with respect to the host’s memory utilization in an effort to prevent excessive page faulting.

Many disk drive-based caches use prefetching techniques to reduce disk accesses. Prefetching is conceptually similar to CPU-to-memory caching: Both leverage the principles of locality for better performance. When using prefetching, a disk reads a number of sectors subsequent to the one requested with the expectation that one or more of the subsequent sectors will be needed “soon.”

Empirical studies have shown that over 50% of disk accesses are sequential in nature, and that prefetching increases performance by 40%, on average.

The downside of prefetching is the phenomenon of cache pollution. Cache pollution occurs when the cache is filled with data that no process needs, leaving less room for useful data. As with main memory caches, various replacement algorithms are employed to help keep the cache clean. These strategies include the same ones used by CPU-to-memory caches (LRU, LFU, and random). Additionally, because disk caches serve as a staging area for data to be written to the disk, some disk cache management schemes simply evict all bytes after they have been written to the disk.

The fundamental difference between reading data from and writing data to the disk gives rise to a number of thorny cache issues. First and foremost is the problem that cache is volatile memory. In the event of a massive system failure, data in the cache is lost. Suppose an application running on the host believes that the data has been committed to the disk, when it really is resident only in the cache. If the cache fails, the data just disappears. This, of course, can lead to serious data inconsistencies, such as an ATM dispensing money without debiting the customer’s account.

To defend against power loss to the cache, some disk controller-based caches are mirrored and supplied with a battery backup. When a cache is mirrored, the controller contains two identical caches that operate in tandem, both containing the same data at all times. Another approach is to employ the write-through cache discussed in Chapter 6, where a copy of the data is retained in the cache in case it is needed again “soon,” but it is simultaneously written to the disk. The operating system is signaled that the I/O is complete only after the data has actually been placed on the disk. Performance is compromised to some extent to provide better reliability.

When throughput is more important than reliability, a system may employ the write back cache policy. Recall that there are two types of write back policies. The simplest is where the disk simply reads the cache periodically (usually twice a minute), and writes any dirty blocks that it finds to the disk. If reliability is a concern, the commitment interval can be made shorter (at the expense of performance). A more complex write back algorithm uses opportunistic writes. With this approach, dirty blocks wait in the cache until the arrival of a read request for the same cylinder. The write operation is then “piggybacked” onto the read operation. This approach has the effect of reducing performance on reads, but improving it for writes. Many systems combine periodic and opportunistic write back policies to try to strike a balance between efficiency and reliability.

The tradeoffs involved in optimizing disk performance present difficult choices. Our first responsibility is to assure data reliability and consistency. But the highest throughput is realized when volatile caches compensate for access time delays. Caches with battery backups are costly. Adding disks to increase throughput is also an expensive option. Removing cache intermediaries from disk write operations may result in performance degradation, particularly if disk utilization rates are high. Users will soon complain of lengthy responsive times and financial people will complain when you ask them for money for a disk upgrade. Keep in mind that no matter what its price, upgrading a disk subsystem is always cheaper than replacing lost data.

Chapter Summary

This chapter has presented the two aspects of computer performance: performance assessment and performance optimization. You should come away from this chapter knowing the key measurements of computer performance and how to correctly summarize them. Specifically, you should know that arithmetic averages are not appropriate for highly variable data and should not be used with rates or ratios. The geometric mean is useful when data are highly variable, but this mean cannot be used to predict performance. The harmonic mean is appropriate when comparing rates, and it is also useful as a performance predictor. However, when the harmonic mean is used to compare relative system performance, it is more sensitive to the choice of a reference machine than the geometric mean.

We have explained a number of the more popular benchmarking programs and suites in this chapter. The most reliable of these are the benchmarks that are formulated and administrated by impartial oversight bodies such as SPEC and the TPC. Regardless of which ones you use, benchmarks should be interpreted in terms of your specific application. Remember, there is no single metric that is universally applicable to all situations.

Computer performance is directly dependent on computer component optimization. We examined the factors that influence the performance of the principal computer system components. Amdahl’s Law gives us a tool for determining the potential speedup due to various optimization techniques and places a ceiling on performance enhancements. Areas to consider for optimization include CPU performance, memory performance, and I/O. CPU performance is dependent on the program code, the compiler technology, the ISA, and the underlying technology of the hardware. Branch instructions have a dramatic effect on pipeline performance, which in turn has a significant effect on CPU performance. Branch prediction is one way to offset the complications introduced by branching. Fixed and static methods of branch prediction are less accurate than dynamic techniques, but are attainable at a lower cost.

I/O performance is a function of both the logical and physical characteristics of disk drives. Short of replacing the hardware, we are unable to improve physical disk performance. But many aspects of logical disk performance lend themselves to tuning and optimization. These factors include disk utilization, file placement, and memory cache sizes. Good performance reporting tools not only provide thorough I/O statistics, but they also offer tuning suggestions.

System performance evaluation and optimization are two of the most important tasks of system managers. In this chapter, we have presented only general platform-independent information. Some of the most helpful and interesting information is found in vendor-provided manuals and training seminars. These resources are essential to the continued effectiveness of your system tuning efforts.

Review Of Essential Terms And Concepts

1. Explain what is meant when we say that a program or system is memory bound. What other types of bindings have we discussed?

2. What does Amdahl’s Law tell us about performance optimization?

3. Which of the means is useful for comparing rates?

4. For what kinds of data is the arithmetic mean inappropriate?

5. Give a definition for optimum performance.

6. What is a price-performance ratio? What makes it hard to apply?

7. What is the shortcoming of using MIPS or FLOPS as a measure of system throughput?

8. How is the Dhrystone benchmark different from Whetstone and Linpack?

9. What are the deficiencies in the Whetstone, Dhrystone, and Linpack benchmarks that are addressed by the SPEC CPU benchmarks?

10. Explain the term benchmarketing.

11. How is the focus of the TPC different from SPEC?

12. Explain delayed branching.

13. What is branch prediction? What is it used for?

14. Give three examples of pipeline hazards.

15. Define the terms loop fusion, loop fission, loop peeling, and loop interchange.

16. According to queuing theory, what is the critical disk utilization percentage?

17. What is the risk involved in using the SSTF disk scheduling algorithm?

18. How is LOOK different from SCAN?

19. What is disk prefetching? What are its advantages and disadvantages?

20. What are the advantages and disadvantages of caching disk writes?

Exercises

1. Hints and Answers Table 10.2 shows an execution mix and run times for two computers, System A and System C. In this example System C is 83% faster than System A. Table 10.3 shows run times for System A with a different execution mix. Using the execution mix in Table 10.3, calculate the percentage by which System C would be faster than System A. Using the original statistics from Table 10.2, by how much has the performance of System A degraded under the new execution mix?

2. With regard to the performance data cited for programs v, w, x, y, and z in Section 10.3, find the geometric means of the run times of the programs for System B and System C, using System A as the reference system. Verify that the ratios of the means are consistent with the results obtained using the other two systems as reference systems.

3. Hints and Answers The execution times for three systems running five benchmarks are shown in the table below. Compare the relative performance of each of these systems (i.e., A to B, B to C, and A to C) using the arithmetic and geometric means. Are there any surprises? Explain.

   

4. The execution times for three systems running five benchmarks are shown in the table below. Compare the relative performance of each of these systems (i.e., A to B, B to C, and A to C) using the arithmetic and geometric means. Are there any surprises? Explain.

   

5. A company that is selling database management optimization software contacts you to pitch its product. The representative claims that the memory management software will reduce page fault rates for your system. She offers you a 30-day free trial of this software. Before you install it, however, you decide to first determine a baseline for your system. At specific times of the day, you sample and record the page fault rate of your system (using the system’s diagnostic software). You do the same after the software has been installed. How much of an average performance improvement has the new software provided?

   The fault rates and times of day are shown in the table below.

   

6. What are the limitations of synthetic benchmarks such as Whetstone and Dhrystone? Do you think that the concept of a synthetic benchmark could be extended to overcome these limitations? Explain your answer.

7. Hints and Answers What would you say to a vendor that tells you that his system runs 50% of the SPEC benchmark kernel programs twice as fast as the leading competitive system? Which statistical fallacy is at work here?

8. Suppose that you are looking into purchasing a new computer system. You have suitable benchmark results for all of the systems that you are considering except for System X Model Q. The benchmark results have been reported for System X Model S, and they are not quite as good as several competing brands. In order to complete your research, you call the people at System X computer company and ask when they plan to publish benchmark results for the Model Q. They tell you that they will not be publishing these results anytime soon, but because the disk drives of Model Q give an average access time of 12ms, while Model S had 15ms drives, Model Q will perform better than Model S by 25%. How would you record the performance metrics for System X model Q?

9. Hints and Answers What value do you think there would be in comparing the results of two different SPEC CPU releases, say, SPEC95 with SPEC2000?

10. Besides the retail business sector, what other organizations would need good performance from a transaction-processing system. Justify your answer.

11. Hints and Answers Which of the benchmarks discussed in this chapter would be most helpful to you if you were about to purchase a system to be used in DNA research? Why would you choose this one? Would any of the other benchmarks be of interest to you? Why or why not?

12. Suppose a friend has asked you to help him make a choice as to what kind of computer he should buy for his personal use at home. What would you look for in comparing various makes and models? How is your line of thinking different in this situation than if you were to help your employer purchase a Web server to accept customers’ orders over the Internet?

13. Hints and Answers Suppose you have just been assigned to a committee that has been tasked with purchasing a new enterprise file server that will support customer account activity as well as many administrative functions, such as producing a weekly payroll. (Yes, a committee frequently makes these decisions!) One of your committee members has just learned that a particular system has blown out the competition in the SPEC CPU2000 benchmarks. He is now insisting that the committee buy one of these systems. What would be your reaction to this?

14. * We discussed the limitations of the harmonic mean in its application to computer performance assessment. A number of critics have suggested that the SPEC should use the harmonic mean instead. Suggest a unit of “work” that would be appropriate for reformulating the SPEC benchmarks as rate metrics. Test your theory using results from SPEC’s Web site, www.spec.org.

15. * SPEC and the TPC both publish benchmarks for Web server systems. Visit the respective Web sites of these organizations (www.spec.org and www.tpc.org) to try to find identical (or comparable) systems that have results posted on both sites. Discuss your findings.

16. We mentioned that a large volume of data is gathered during system probe traces. To give you some idea of the actual volume of data involved, suppose plans are being made to install a hardware probe that reports the contents of a system’s program counter, instruction register, accumulator, memory address register, and memory buffer register. The system has a clock that runs at 1GHz. During each cycle of the system clock, the status of these five registers is written to nonvolatile memory attached to the probe circuitry. If each register is 64 bits wide, how much storage will the probe require if it is to gather data for 2 seconds?

17. The sidebar in Section 10.5.2 presents ways in which program performance can be improved. For each of the tips in the sidebar, state whether a computer organization and architecture issue is involved. If so, explain the reasoning behind the advice as given. If you feel anything is missing from the sidebar, include your advice in your analysis.

18. In our discussion of the physical aspects of disk performance, we stated that replacing 7200 RPM disks with 10,000 RPM disks can bring a 10% to 50% performance improvement. Why would an improvement of only 10% occur? Could it be that no improvement at all would occur? Explain.

19. Calculate the number of disk tracks traversed using the FCFS, SSTF, SCAN, and LOOK algorithms for the series of disk track service requests given below. At the time the first request arrives in the disk request queue, the read/write head is at track 50, moving toward the outer (lower-numbered) tracks. (Hint: Each track over which the disk arm passes counts in the total, whether or not the track is read.)

    54, 36, 21, 74, 46, 35, 26, 67

20. Repeat the previous problem using the following tracks:

    82, 97, 35, 75, 53, 47, 17, 11

21. On a particular brand of disk drive, the time that it takes for the disk arm to pass over a single disk track without stopping is 500 nanoseconds. However, once the head reaches the track for which it has a service request, it needs 2 milliseconds to “settle” over the required track before it can start reading or writing. Based on these timings, compare the relative times required for FCFS, SSTF, and LOOK to carry out the schedule given below. You will need to compare SSTF to FCFS, LOOK to FCFS, and LOOK to SSTF.

    As in our previous question, when the first request arrives in the disk request queue, the read/write head is at track 50, moving toward the outer (lower-numbered) tracks. The requested tracks are: 35, 53, 90, 67, 79, 37, 76, 47

22. Repeat Exercise 21 for the following disk tracks (assuming the read/write head is at track 50, moving outward):

    48, 14, 85, 35, 84, 61, 30, 22

23. * In our discussion of the SSTF disk scheduling algorithm, we stated that the problem of starvation “is at its worst with low disk utilization rates.” Explain why this is so.

24. A certain microprocessor requires either 2, 3, 4, 8, or 12 machine cycles to perform various operations. Twenty-five percent of its instructions require 2 machine cycles, 20% require 3 machine cycles, 17.5% require 4 machine cycles, 12.5% require 8 machine cycles, and 25% require 12 machine cycles.

    1. Hints and Answers What is the average number of machinecycles per instruction for this microprocessor?

    2. Hints and Answers What is the clock rate (machine cycles per second.) required for this microprocessor to be a “1 MIPS” processor?

    3. Hints and Answers Suppose this system requires an extra 20 machine cycles to retrieve an operand from memory. It has to go to memory 40% of the time. What is the average number of machine cycles per instruction for this microprocessor, including its memory fetch instructions?

25. A certain microprocessor requires either 2, 4, 8, 12, or 16 machine cycles to perform various operations. Seventeen and one-half (17.5.) percent of its instructions require 2 machine cycles, 12.5% require 4 machine cycles, 35% require 8 machine cycles, 20% require 12 machine cycles, and 15% require 16 machine cycles.

    1. What is the average number of machine cycles per instruction for this microprocessor?

    2. What is the clock rate (machine cycles per second.) required for this microprocessor to be a “1 MIPS” processor?

    3. Suppose this system requires an extra 16 machine cycles to retrieve an operand from memory. It has to go to memory 30% of the time. What is the average number of machine cycles per instruction for this microprocessor, including its memory fetch instructions?