Economics and payback
As we h ave seen, producing energy efficient motors with minimal losses req u ires more higher-priced materials, resu lting in a more-costly motor -typi cally 20% to 25% more expensiv e than a standard motor . The red uction in losses will prod uce lower operating power consumption, and thi s must be sufficient to repay the increased initial cost within a reasonable period of tim e. At today’s electric power costs, pay back time for an energy-efficient motor is quite short, and it is difficult to understa nd the relatively slow penetra tion of these motors into the m arket place. For those applications with many hours of operation and high energy costs, only lack of knowl edge can explain the pur ch ase of stand ard motors over available energy-efficien t motors. In 1980 sales of energy-effi cient motors made up only 4 to 5% of the integral-horsepower motor m arket. The Department of Energy expects energy-efficient motors to make up aboui 33% of this market by 1985 and 74 % by 1990.
Operating costs
It is important to recognize that motor operatin g costs are often many times the original cost of the motor . Let us contrast this with a typical family car of today, wh ere purchasers are insisting on increased efficiency as measured in miles-per-gallon (as De troit has learned at great cost). If a car is driven 15,000 miles a year and deliv ers 20 miles per gallon, it will consume 750 gallons of gasoline. At an average $1.25 per gallon, this amounts to $938 per yea r for fuel. If the car cost $7000, th en th e annual fuel cost is about 13% of the purchase price. By comparison , a 20-hp motor with an average standard efficiency of 88% costs about $450 and consum es abou t 17 kW of power. If this motor operates two shifts a day, 80 hours a week, for 50 weeks a year, it would run 4000 hours a year and con sume 68,000 kWh. At an average 4¢ per kWh, the energy to operate this motor would cost $2720 a year-over 6 times the pw·chase price of the motor. Losses alone, at 12%, would cost $326 a year. In 1112 years the cost of losses exceeds the price of a new motor. (See Table 2.) An energy-efficient motor, with an efficiency of 92%, would have losses of only 8%, one-third less than the standard motor. This would result in a saving of $118 per year in energy costs, but the motor would cost $112 (about 25%) more. The energy-effi cient motor would recover its addition al cost in the first year of operation, which is not exceptional. Usually pay-back periods range from 1 to 2 years for the extra cost of energy-efficient motors. After that time, the power saving would continue for the life of the motor. In 20 years the saving would total 51 times the original cost of the motor and 21 times the premium paid for the energy-efficient motor.
Economic analysis
The preceding example was a very basic comparison of motor initial and operating costs to obtain an estimate of the time required by an energy-effi cient motor to pay back its extra cost. Often this simple payback calculation is enough to justify the purchase of a more-efficient motor. In other cases, a more-comprehensive accounting ap proach may be desired, resulting in a true economic analysis for competing alternatives. This analysis will take into account the true cost of electricity, the time value of money, interest rates, income and investment tax consider ations, and similar factors. Annual savings for the typical induction motor will vary with the duty cycle and power rate.
Several methods of evaluating the saving from energy-efficiency motors are shown in Fig. 4. The annual operat ing cost for each 1\lOtor being compared is calculated first. The annual cost sav ing is the difference in operating cost between the lower-efficiency (or stan dard) ·and higher-efficiency motors. Even this simple calculation assumes a known and constant cost of electric energy. The true cost of electric energy, it must be understood, is not merely the charge per kilowatt-hour. It must also include demand charges, fuel adjustment charges, power-factor pen alties, and all other charges billed by the utility. If the power is onsite-gener ated rather than purchased from a utility, the true cost of that power is even more difficult to calculate. In determining costs over a period of years, allowance must be made for the increase in pmver costs with rising fuel prices and inflation. (If the utility charges a power-factor penalty, and the operating power factor is low enough to incur such a penalty, a wise investment would be PF correction capacitors, which would probably pay for themselves in less than two years, independent of any motor loss costs.)
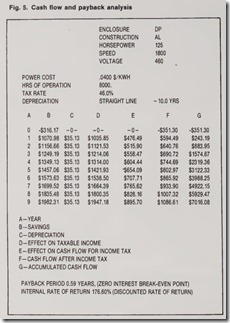
Once the annual saving is computed, the simplest method of calculating the payback time is to see how many years (or months) it takes for these savings to equal or exceed the price premium paid for the energy-efficient motor. This method, while uncomplicated, ignores the fact that if this additional money were not spent on the higher cost motor, it could be put to work earning interest or invested in produc tion and earning profit. Therefore, especially at today’s high interest rates and cost of money, the present value or present worth of these anticipated
annual savings must be calculated. For example, if the saving equalled $100 per year for 10 years, the simple pay back method would assume a saving of $1000. Taking interest into consider
ation and assuming a very low (for today) interest rate of 12% , the pre sent worth of $100 per year for 10 years at 12% annually (from published compound interest tables) is only $565.
To get a realistic appraisal of the value of the power savings for an ener gy-efficient motor over a selected peri od of time, not only must the interest rate be predicted; the inflationary increase in the cost of power, the effect of taxes, investment tax credits, depre ciation, and the like must also be factared into the calculation to some degree. This is difficult, but computer programs have been developed that do these complex calculations once the user selects his parameters. One manu facturer of energy-efficient motors has equipped his sales force with portable computer terminals. The salesman will come to you, connect his portable ter minal to your telephone, and call his company’s computer. You select inter est rates, inflation rates, period of time, motor horsepower, annual hours of use and similar data, and the desired method of calculation, from the sim plest to the most complex. The comput er terminal will print out a complete annual savings, cash flow, and payback analysis. The computer program can factor in depreciation methods, tax rates, investment-tax credits, fuel-cost increases and similar data. It can then provide such information as dis counted-investment payback, life-cycle costs, and after-tax cash flow. A com puter printout from this program is similar to that shown in Fig. 5.
Whether payback calculations are done simply or include all complex fac tors, it is apparent that where annual hours of operation are high, energy efficient motors are a sound invest ment when a new motor is to be pur chased. What is less obvious is that in many cases it is economically sound to replace an existing motor, especially one which, while satisfactorily opera tional, has been fully depreciated. In addition to the substantial saving in electric energy gained by replacing the motor with a more-efficient one, the new motor can be depreciated over its new life, and some investment tax credits may be available. The computer program can make it possible to exam ine the economics of a situation such as this .
When a motor fails, it can either be replaced or, as frequently is the case for larger motors, rewound. Many industrial users today have decided that all replacement motors purchased shall be of the energy-efficient design. Again, the computer program can help in deciding whether to rewind the motor or replace it with a more efficient unit. One important consider ation in this decision is that rewinding a motor may cause a lowering of its efficiency, increasing the losses. It has been fgund that in heating the core to remove the old coils sometimes excess heat is used. This can deteriorate the insulating surfaces between the laminations and substantially increase eddy-current core losses.
A major rubber company had many identical 30-hp motors in one plant, and when one failed it was replaced by a spare and then rewound. It was noticed that these originally identical motors were drawing different cur rents under the same load, and study showed that the current increased with each rewinding as efficiency decreased. This company decided that the increase in losses made it no }anger economical to rewind these motors and replaced them with new motors as they failed. Remember that an increase of even 1% or 2% in losses can cost a tremendous amount over the life of the motor often many times the cost of the motor
itself. This small increase in losses may not be noticed as increased current in the rewound motor. The Electrical Apparatus Service Association (EASA) is doing some testing to deter mine the severity of this problem, since little data is available. Use of mini mum heat and maximum care in removing old coils, protecting the core from damage, will result in the least effect on efficiency of the rewound motor but will increase the cost of rewinding. Motor rewinding shops usu ally are not equipped to measure the efficiency of a motor that has been rewound.
Purchasing an efficient motor.
In deciding whether to purchase an energy-efficient motor, it is important to make valid comparisons. In actually purchasing the motor, it is important that the desired efficiency level be achieved. This is still not simple, although recent standardization of measurement methods has improved the situation. It is extremely impor tant, as explained in Part 1 of this series, that efficiency be measured by IEEE Standard 112, Method B, as modified by NEMA Standard MG1- 12.53(a) and (b) in all cases.
Defining efficiency
The word “efficiency” applied to motors must be very carefully defined, as we saw in Part 1. Let us look at some of the terminology in use.
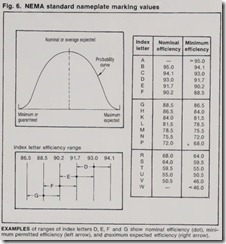
Nominal or average expected efficiency is the average value of a large number of motors of the same make and model. Individual motors can vary widely from this average, and this effi ciency cannot be relied upon in eco nomic determinations.
Calculated efficiency is just that calculated from motor parameters and numerous assumptions. It often bears little resemblance to measured effi ciency and should not be used for loss determinations.
Apparent efficiency is the product of motor power factor and efficiency. A guaranteed apparent efficiency tells the motor user nothing reliable in figu ring costs, since it could come from a high power factor and low efficiency or from a low power factor and high effi ciency or from something in between.
Minimum or expected m1:nimum efficiency is a little more sharply defined. All motors should be equal to or higher than the efficiency value given. However, there can be some question even here. One motor manu facturer defines “minimum” as the val ue that 95% of his motors will meet.
Gua.ranteed minimum efficiency is the value that the manufacturer guar antees all motors of that rating will meet or exceed. At least one manufac turer warrants that if his motor does not meet the guaranteed efficiency, he will replace or repair the motor or pay the user a cash sum to compensate for the additional losses.
When evaluating different motors, these guaranteed minimum values must be compared to obtain reliable cost figures. Care must be taken not to compare minimum values with nomi nal, average, or nonguaranteed values. One or two percentage points of error in efficiency can result in thousands of dollars difference in savings over the life of a motor.
NEMA standards
Normal variations in materials, manufacturing processes, and testing of motors result in a range of Afficien cies for a large batch of motors of the same design. Recognizing this, NEMA Standard MGl-112.53 (b) has been established. It is based on the normal statistical bell-shaped probability curve, which assumes that for a given design half the motors will be above and half below the nominal or average efficiency. The manufacturer must measure the efficiency by means of IEEE 112 Method B, as modified by NEMA MG1-12.53(a) and (b). He may then put a code index letter on the motor nameplate (Fig. 6), which wi!J indicate both the nominal efficiency for that motor design and the minimum efficiency for any individual motor of that design. Some manufacturers mark the nameplate with the efficiency in percent, rather than with a code letter. In this case it is extremely important that the user determine whether this value is nominal or minimum efficien cy. A manufacturer should, in any case, be willing to guarantee the minimum efficiency of his motor.