Frequency Response and Linearity
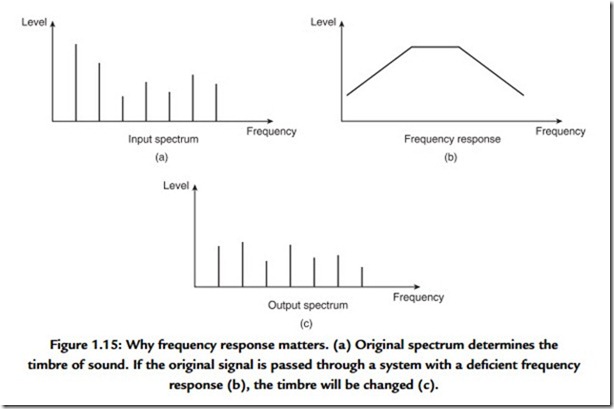
It is a goal in high-quality sound reproduction that the timbre of the original sound shall not be changed by the reproduction process. There are two ways in which timbre can inadvertently be changed, as Figure 1.15 shows. In Figure 1.15(a), the spectrum of
the original shows a particular relationship between harmonics. This signal is passed through a system [Figure 1.15 (b)] that has an unequal response at different frequencies.
The result is that the harmonic structure [Figure 1.15(c)] has changed, and with it the timbre. Clearly a fundamental requirement for quality sound reproduction is that the response to all frequencies should be equal.
Frequency response is easily tested using sine waves of constant amplitude at various frequencies as an input and noting the output level for each frequency.
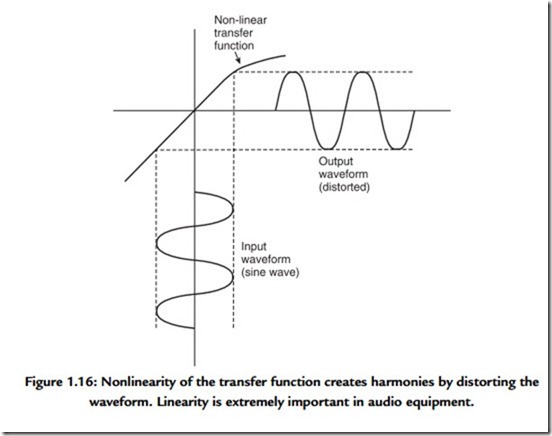
Figure 1.16 shows that another way in which timbre can be changed is by nonlinearity. All audio equipment has a transfer function between the input and the output, which form the two axes of a graph. Unless the transfer function is exactly straight or linear, the output waveform will differ from the input. A nonlinear transfer function will cause distortion, which changes the distribution of harmonics and changes timbre.
At a real microphone placed before an orchestra a multiplicity of sounds may arrive simultaneously. Because the microphone diaphragm can only be in one place at a
time, the output waveform must be the sum of all the sounds. An ideal microphone connected by ideal amplification to an ideal loudspeaker will reproduce all of the sounds simultaneously by linear superimposition. However, should there be a lack of linearity anywhere in the system, the sounds will no longer have an independent existence, but will interfere with one another, changing one another’s timbre and even creating new sounds that did not previously exist. This is known as intermodulation. Figure 1.17 shows that a linear system will pass two sine waves without interference. If there is any nonlinearity, the two sine waves will intermodulate to produce sum and difference frequencies, which are easily observed in the otherwise pure spectrum.